- Extinction : \( p_n \rightarrow 0 \: ? \)
- Stabilisation : \( p_n \rightarrow p_\infty \in ]0,+\infty[ \: ? \)
- Explosion : \( p_n \rightarrow + \infty \: ? \)




Cette U.E. de "culture mathématique" aura pour objet de revisiter, et parfois d'approfondir, plusieurs concepts mathématiques rencontrés au cours du programme du premier semestre de L1 (et des années précédentes). On s'efforcera de montrer comment les outils mathématiques développés dans le tronc commum permettent d'étudier des problèmes non triviaux, le but n'étant pas d'anticiper sur le programme des années suivantes, mais plutôt de s'intéresser à des questions "transversales" qui font partie d'une culture générale en mathématiques sans toujours figurer explicitement dans le programme d'une UE donnée. La bonne maîtrise du tronc commun est donc un prérequis fondamental dans cette UE. A titre d'exemples, on s'intéressera à quelques modèles simples en dynamique des population ; on étudiera des sytèmes fermés à deux ou trois états en se concentrant sur leur comportement asymptotique ; on s'intéressera aux probabilités de différentes figures dans le jeux de YAMS ; on parlera de méthode de Newton pour approcher numériquement une solution d'une équation donnée (comparaison avec la méthode par dichotomie, sensibilité à la condition initiale).
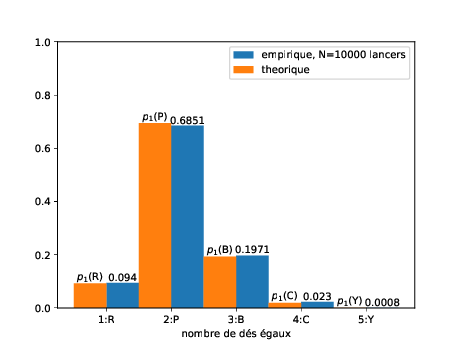
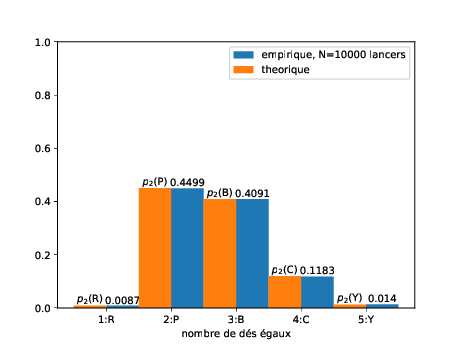
Le jeu de YAMS consiste à lancer 5 dés simultanément et observer les figures obtenues : selon les variantes, paire, double paire, brelan, full, suite, carré et lorsque les 5 dés affichent la même valeur, on a réussi un yams ! Comme on l’imagine et on va le vérifier, obtenir un yams en un lancer est assez rare, cependant le jeu permet de choisir tout ou partie des dés et de les relancer afin d’améliorer la figure obtenue. Une stratégie assez naturelle afin d’essayer d’obtenir un yams est alors la suivante :
- si tous les dés ont des valeurs différentes, on relance tous les dés,
- sinon on garde un maximum de dés de même valeur et on relance les autres.
Quelle est la probabilité d’obtenir un yams après ce deuxième lancer ?
La Méthode de Newton permet de calculer une solution approchée d'une équation de la forme \( f(x) = 0 \). On rappelle qu'on ne sait résoudre explicitement une telle équation que dans très peu de cas : si \( f \) est linéaire, si \( f \) est un polynôme de degré 2, et il existe encore des formules à base de radicaux (i.e. des formules faisant uniquement intervenir les coefficients du polynôme, les quatre opérations élémentaires et les racines k-ièmes) jusqu'à l'ordre 4 mais pas pour les polynômes de degré supérieur à 5, comme l'a montré le mathématicien Abel.
Il est alors naturel de se poser la question de la résolution approchée d'une telle équation. La méthode de Newton fournit une méthode, et même une famille de méthodes, dont l'avantage incontestable est la rapidité de convergence (convergence quadratique). Malheureusement, la convergence n'est en général garantie que si l'on connaît déjà une assez bonne approximation de la solution que l'on recherche (on parle de convergence locale), qui est l'inconvénient principal de la méthode de Newton. À noter que sous hypothèse de convexité, il est possible d'obtenir des résultats de convergence globale et de réconcilier ainsi rapidité et robustesse de la méthode.
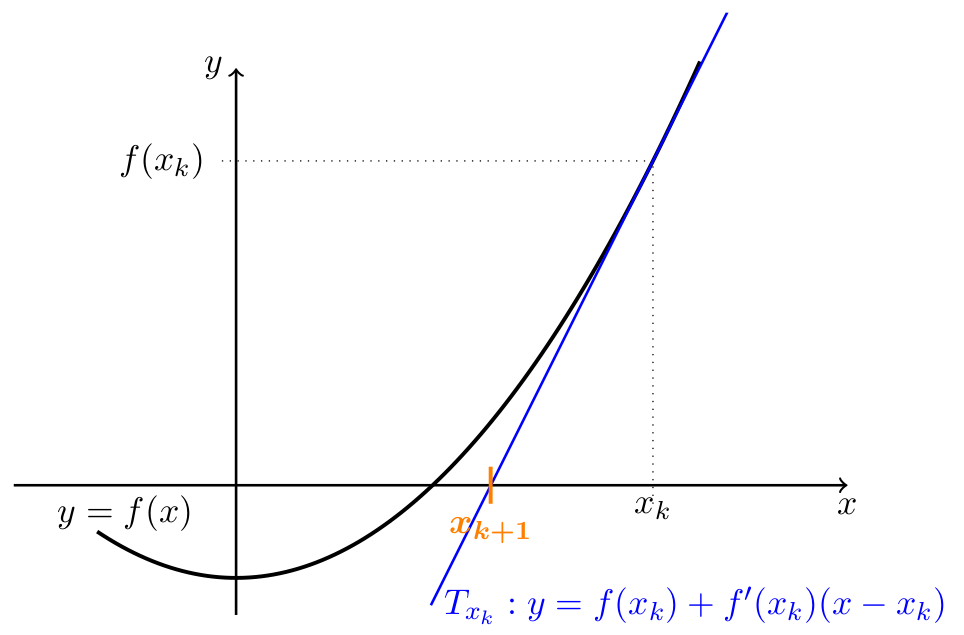
Principe : Soit \(f : I \subset \mathbb{R} \rightarrow \mathbb{R} \) et supposons que l'on cherche une solution de l'équation \( f(x) = 0 \) dans l'intervalle \( I \) et partant de \( x_0 \in I \) (par exemple une approximation grossière obtenue par dichotomie). L'idée de la méthode de Newton est de linéariser l'équation \( f(x) = 0 \) au voisinage de \( x_0 \) et de résoudre l'équation affine $$ f(x_0) + f^\prime (x_0)(x-x_0) = 0 \: . $$ Si \( f^\prime(x_0) \neq 0 \), on peut ainsi définir $$ x_1 = x_0 - \frac{f(x_0)}{f^\prime(x_0)} $$ et recommencer en linéarisant autour de \( x_1 \), pourvu qu'on ait bien \( x_1 \in I \). On obtient la méthode itérative $$ \left\lbrace \begin{array}{l} x_0 \in I \\ x_{k+1} = x_k - \displaystyle \frac{f(x_k)}{f^\prime(x_k)}, \, k \in \mathbb{N} \end{array} \right. . $$
Géométriquement, l'équation \( y = f(x_k) + f^\prime (x_k)(x-x_k) \) est l'équation de la tangente \( T_{x_k} \) à la courbe représentative de \( f \) au point \( (x_k, f(x_k)) \), de sorte que \( x_{k+1} \) est le point d'intersection entre \( T_{x_k} \) et l'axe des abscisses.
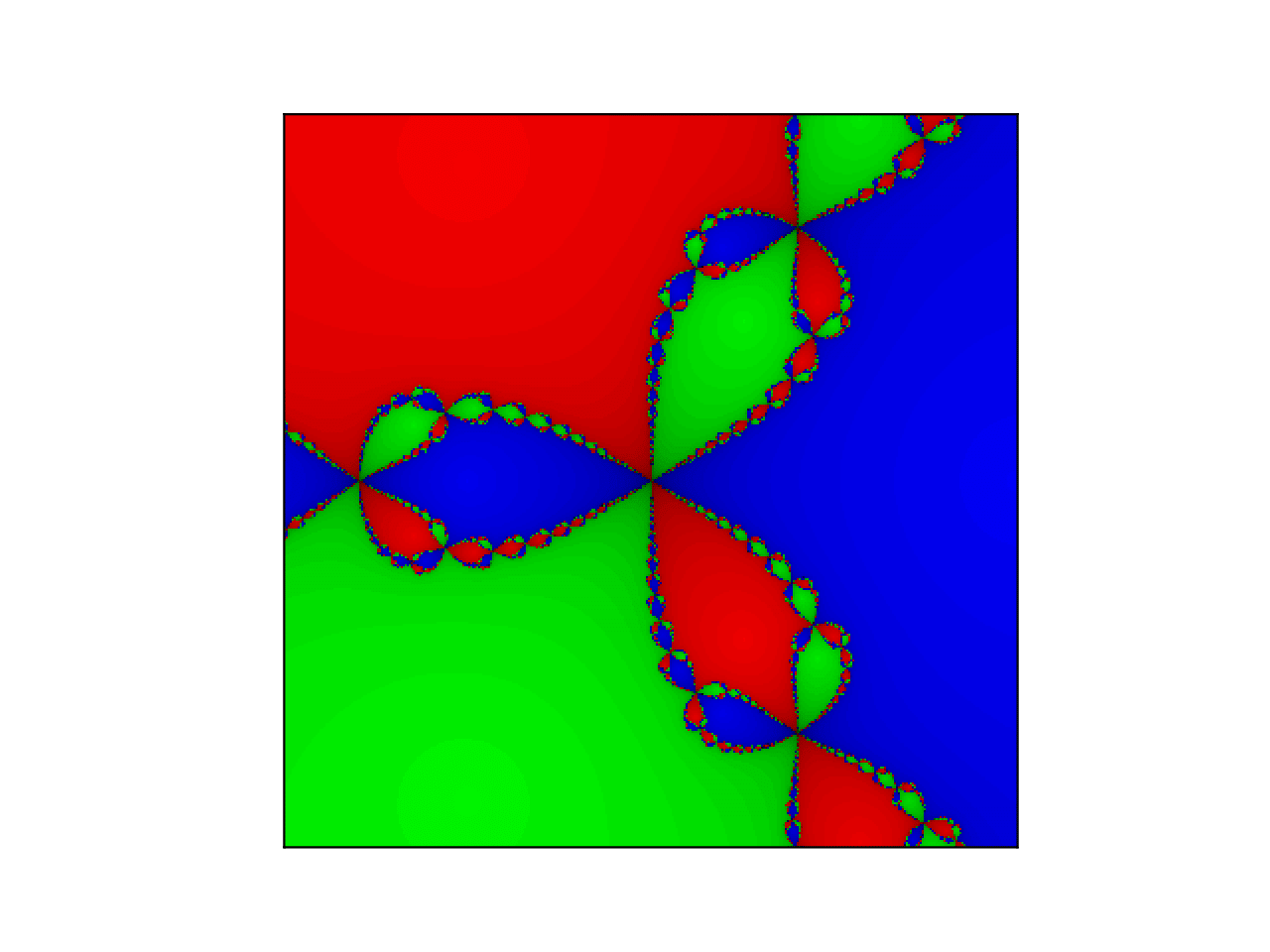
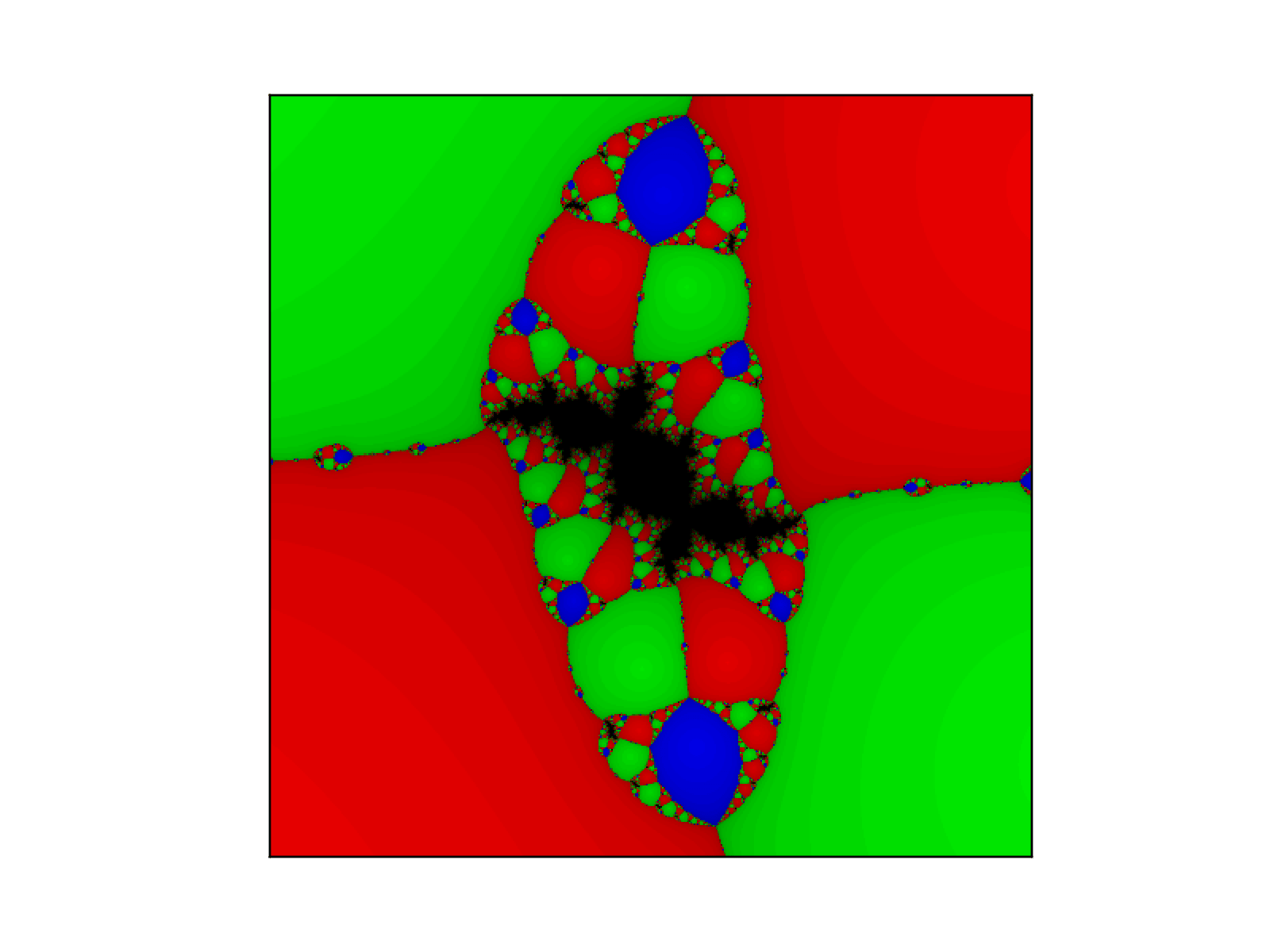
Prenons l'exemple d'un modèle d'épidémie à trois états : chaque individu peut-être malade (M), immunisé (I) ou sain mains non immunisé (S). D'une semaine à l'autre,
Les proportions de la population dans chacun des états (M) malades, (I) immunisés, (S) sains mais non immunisés, se stabilisent-elles une fois que l'épidémie s'est installée (quand \( k \to +\infty \)) ? si oui, quelles proportions obtient-on ?
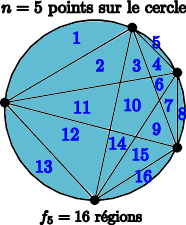
Problème : on place n points sur un cercle et on trace ensuite toutes les cordes joignant deux points distincts. Combien de régions a-t-on ainsi créées dans le disque ? On supposera que trois cordes distinctes ne se croisent jamais en un même point...
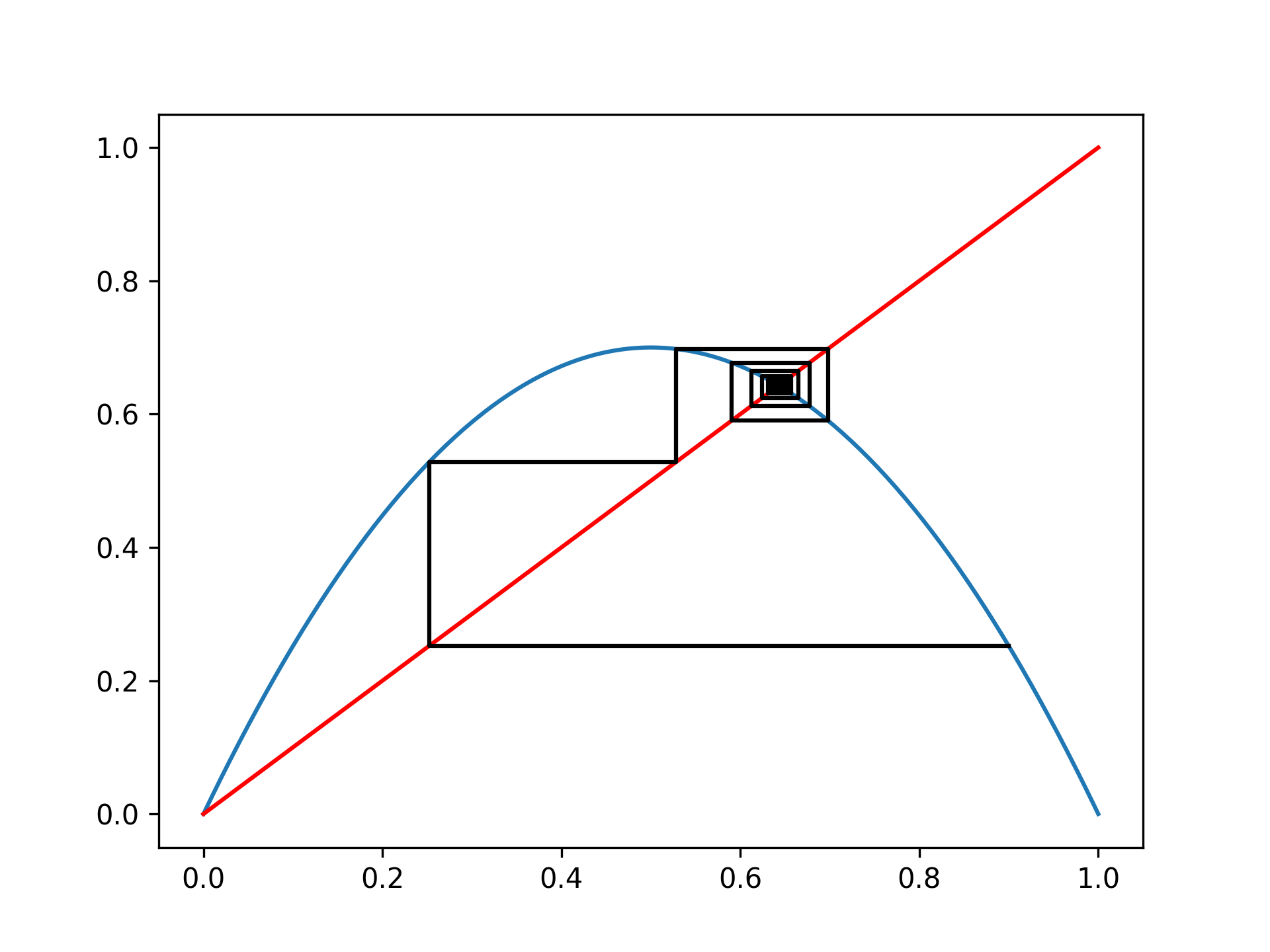
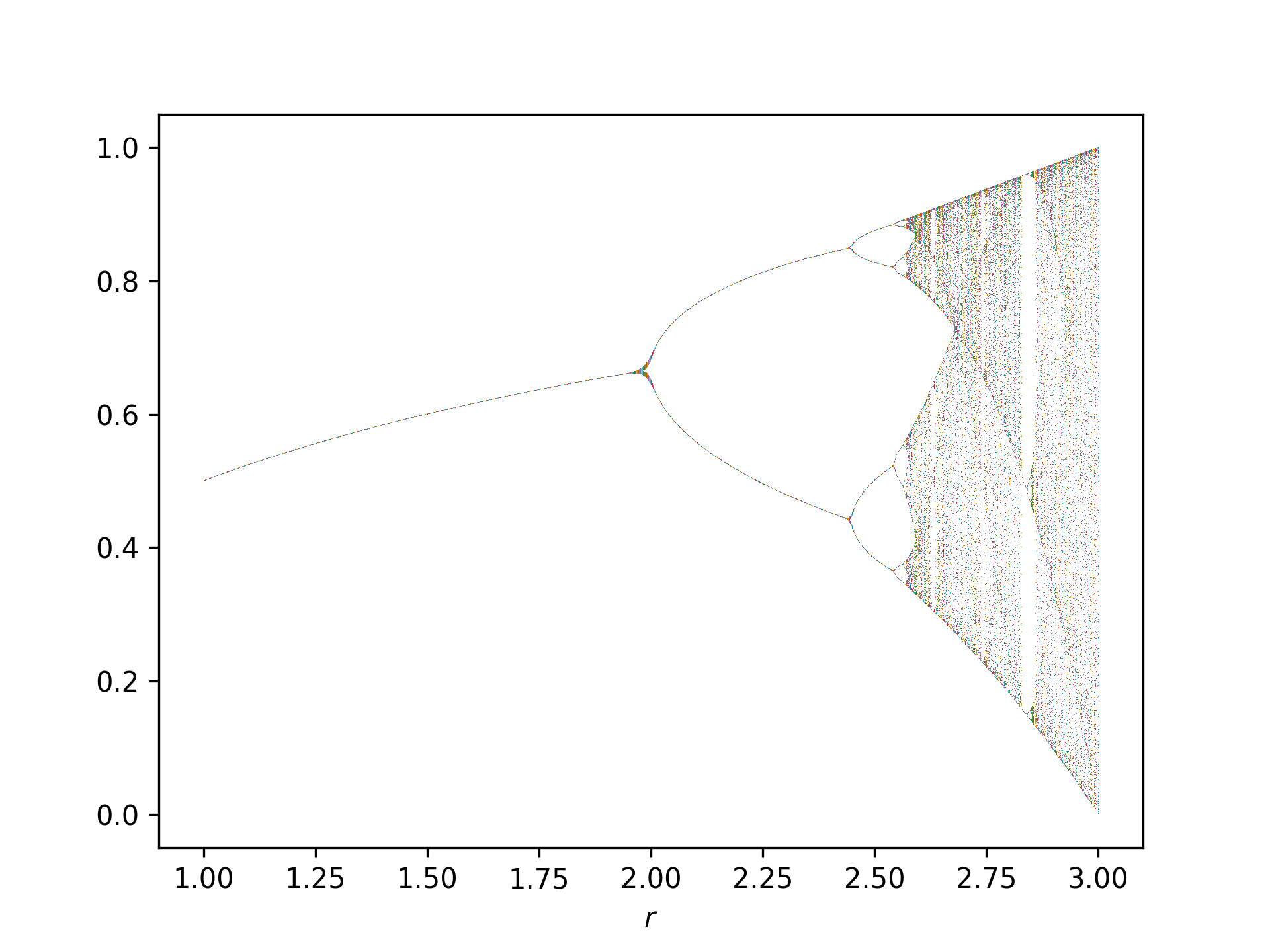
On étudie le ``système dynamique'' associé à $$ \begin{array}{lcccl} g & : & [0,1] & \rightarrow & [0,1] \\ & & x & \mapsto & 4 x (1-x) \end{array} $$ On va montrer qu'il existe \( \alpha \in [0,1] \) tel que la suite \( (x_n)_{n \in \mathbb{N}} \) définie par $$ \left\lbrace \begin{array}{lcl} x_0 & = & \alpha \\ x_{n+1}& = & g(x_n) \end{array} \right. $$ est dense dans [0,1]. On va même montrer que l'ensemble $$ \left\lbrace \alpha \in [0,1] \: \left| \right. \mbox{ la suite } (x_n)_n \mbox{ definie par } x_0 = \alpha \mbox{ et } \forall n \in \mathbb{N}, \; x_{n+1} = g(x_n) \mbox{ est dense dans } [0,1] \right\rbrace $$ est lui-même dense dans [0,1]. On dit alors que le système dynamique associé à \( g \) est "chaotique". Afin de prouver ce résultat, on va s'intéresser au nombre de Champernowne (une variante de ce nombre) m qui est défini via son développement en base 2 de la façon suivante: m est obtenu en concaténant, après la virgule, toutes les suites possibles formées d'un chiffre dans {0,1}, puis de 2 chiffres, puis de 3 chiffres etc. de sorte que le début du développement dyadique (en base 2) de m est $$ m = 0,\underbrace{0 \: 1}_{1} \underbrace{00 \: 01 \: 10 \: 11}_{2} \underbrace{000 \: 001 \: 010 \: 011 \: 100 \: 101 \: 110 \: 111}_{3} \ldots \: . $$
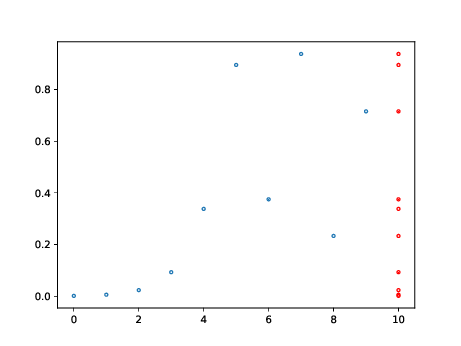
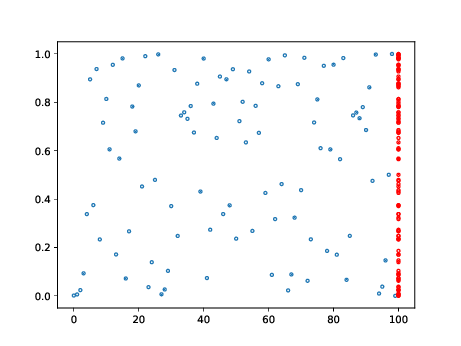
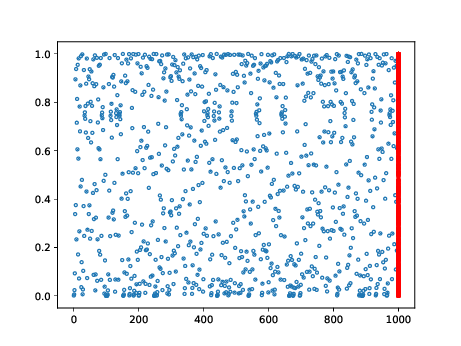
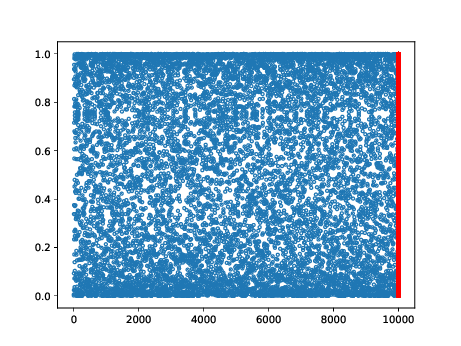 On représente en bleu les points \( (n,x_n) \) pour \( n \) entre 0 et N, et N = 10, 100, 1000, 10000.
On représente en bleu les points \( (n,x_n) \) pour \( n \) entre 0 et N, et N = 10, 100, 1000, 10000.
Le but du Devoir Maison est de montrer que x est rationnel si et seulement si son développement décimal propre est périodique à partir d'un certain rang.
Soit \( q \in \mathbb{N}^\ast \) et \( p_0, p_1, \ldots , p_q \in [0,1] \) tels que \( p_0 + p_1 + \ldots + p_q = 1 \). On considère une population d'individus évoluant au cours des générations. Dans le modèle de Galton-Watson, on passe de la génération n à la génération n+1 de la façon suivante:
Peut-on partitionner le plan avec des cercles ? Et l'espace ?