Chapitre 1 Suites

Définition 1.1 Une suite numérique (ou simplement suite) est la donnée pour tout \(n\in\mathbb{N}\) d’un nombre réel \(x_n\in\mathbb{R}\). On notera alors cette suite \((x_n)_{n\in\mathbb{N}}\) ou simplement \((x_n)\).

Une suite numérique est donc exactement une application de \(\mathbb{N}\) dans \(\mathbb{R}\). On dit que \(x_n\) est le terme général de la suite \((x_n)\).

Exemple 1.1 Voici quelques exemples de suites.

Une suite est arithmétique s’il existe un nombre \(r\in\mathbb{R}\) appelé raison tel que \(x_{n+1}=x_n+r\) pour tout \(n\in\mathbb{N}\).
Une suite est géométrique s’il existe un nombre \(a\in\mathbb{R}\setminus\{0\}\) tel que \(x_{n+1}=ax_n\) pour tout \(n\in\mathbb{N}\).
Notons \(m_n\) le nombre de malades du COVID au \(n\)-ième jour depuis le début de l’épidémie alors \((m_n)_{n\in\mathbb{N}}\) est une suite.
On considère un algorithme de tri de listes. Pour une liste de taille \(n\), on note \(c_n\) le nombre maximal d’opérations à effectuer. Alors \((c_n)\) est une suite.
La suite de Fibonacci se définit de la manière suivante \(u_0=0\), \(u_1=1\) et pour \(n\geq 0\), \(u_{n+2}=u_{n+1}+u_{n}\). Les premiers termes sont donc \[0,1,1,2,3,5,8,13,21,\dots\]

Le _Liber Abaci_ est un livre écrit en 1202 où l'on trouve le problème suivant à l'origine de la suite de Fibonacci : _Quelqu'un a déposé un couple de lapins dans un certain lieu, clos de toutes parts, pour savoir combien de couples seraient issus de cette paire en une année, car il est dans leur nature de générer un autre couple en un seul mois, et qu'ils enfantent dans le second mois après leur naissance._

Figure 1.1: Le Liber Abaci est un livre écrit en 1202 où l’on trouve le problème suivant à l’origine de la suite de Fibonacci : Quelqu’un a déposé un couple de lapins dans un certain lieu, clos de toutes parts, pour savoir combien de couples seraient issus de cette paire en une année, car il est dans leur nature de générer un autre couple en un seul mois, et qu’ils enfantent dans le second mois après leur naissance.

1.1 Monotonie

Définition 1.2 Soit \((x_n)\) une suite numérique.

On dit que \((x_n)\) est croissante si pour tout \(n\leq m\), \(x_n\leq x_m\).

On dit que \((x_n)\) est décroissante si pour tout \(n\leq m\), \(x_n\geq x_m\).

Finalement, on dit qu’une suite est monotone si elle est croissante ou décroissante.

Lemme 1.1 Une suite \((x_n)\) est croissante (respectivement décroissante) si et seulement si pour tout \(n\in\mathbb{N}\), \(x_n\leq x_{n+1}\) (respectivement \(x_n\geq x_{n+1}\)).

Preuve. La preuve est identique pour les suites croissantes et décroissantes. On ne traite que le cas croissant.

Suposons \((x_n)\) croissante. Alors pour \(n\) fixé, on applique la définition de croissance à \(n\) et \(m=n+1\) et on obtient \(x_n\leq x_{n+1}\).

Réciproquement, on suppose que pour tout \(k\in \mathbb{N}\), \(x_k\leq x_{k+1}\). Fixons \(n,m\in\mathbb{N}\) avec \(n\leq m\). Montrons par récurrence sur \(i\in\mathbb{N}\) que \(x_n\leq x_{n+i}\). Pour \(i=0\), on a bien \(x_n=x_{n+0}\) ce qui initialise la récurrence.

On suppose le résultat pour \(i\). Par hypothèse de récurrence, on a \(x_n\leq x_{n+i}\) et a aussi \(x_{n+i}\leq x_{n+i+1}\) donc \(x_n\leq x_{n+i}\leq x_{n+i+1}\) et donc \(x_n\leq x_{n+i+1}\). Ce qui montre l’étape de récurrence. Par principe de récurrence, nous avons bien \(x_n\leq x_{n+i}\) pour tout \(i\in\mathbb{N}\). On applique le résultat à \(i=m-n\in\mathbb{N}\) et on a donc \(n+i=m\) et donc \(x_n\leq x_m\). Ce que l’on voulait montrer.

1.2 Convergence

On rappelle que la valeur absolue d’un nombre réel \(x\) est le nombre positif noté \(|x|\) avec \(|x|=x\) si \(x\geq0\) et \(|x|=-x\) si \(x\leq0\). On a toujours l’inégalité \(x\leq|x|\) et \(|-x|=|x|\). On utilisera souvent des inégalités du type \(|x-y|\leq \varepsilon\), ce qui est équivalent à la double inégalité suivante :

\[-\varepsilon\leq x-y\leq \varepsilon.\] D’autre part, pour un nombre réel \(x\) et un nombre \(A\geq0\), l’inégalité \(|x|\leq A\) est équivalente à \(x\leq A\) et\(-x\leq A\).

Lemme 1.2 (inégalité triangulaire) Soit \(x,y\in\mathbb{R}\), on a \[|x+y|\leq |x|+|y|.\]

Preuve. On sépare en 4 cas selon les signes de \(x\) et \(y\).

Si \(x,y\geq0\) alors \(|x+y|=x+y=|x|+|y|\).
Si \(x,y\leq0\) alors \(|x+y|=|-x-y|\) et on est ramené au cas précédant en considérant \(-x\) et \(-y\) qui sont positifs.
Si \(x\geq0\) et \(y\leq0\) alors \(x+y\leq x=|x|\leq|x|+|y|\) et \(-x-y \leq -y=|y|\leq|x|+|y|\).
Si \(x\leq0\) et \(y\geq0\), on se ramène au cas précédant en échangeant les rôles de \(x\) et \(y\).

Définition 1.3 Une suite \((x_n)\) converge vers une limite \(\ell\) si pour tout \(\varepsilon>0\), il existe \(N\in\mathbb{N}\) tel que pour tout \(n\geq N\), \(|x_n-\ell|\leq\varepsilon\). On notera alors \(\lim x_n=\ell\) ou encore \(x_n\to\ell\).

Une suite qui converge vers une limite est appelée suite convergente.

Lemme 1.3 (Unicité de la limite) Toute suite convergente admet une unique limite.

Preuve. On raisonne par l’absurde. Suppsons que \((x_n)\) admette deux limites \(\ell_1\) et \(\ell_2\) avec \(\ell_1\neq\ell_2\). On applique la définition de limite avec \(\varepsilon=|\ell_1-\ell_2|/3\). Il existe alors \(N_1\) tel que pour tout \(n\geq N_1\) \(|\ell_1-x_n|<\varepsilon\) et \(N_2\) tel que pour tout \(n\geq N_2\) \(|\ell_2-x_n|<\varepsilon\). Posons \(N=\max\{N_1,N_2\}\) alors pour \(n\geq N\), \(|\ell_1-x_n|<\varepsilon\) et \(|\ell_2-x_n|<\varepsilon\). Comme \(|\ell_1-\ell_2|=|\ell_1-x_n+x_n-\ell_2|\), on a \(|\ell_1-\ell_2|\leq|\ell_1-x_n|+|x_n-\ell_2|\) par inégalité triangulaire. Ainsi, \(|\ell_1-\ell_2|\leq2\varepsilon=2/3|\ell_1-\ell_2|\) et comme \(|\ell_1-\ell_2|\neq0\), on obtient la contradiction \(3\leq2\).

Définition 1.4 Soit \(A\in\mathbb{R}\) et \((x_n)\) une suite, on dit que \(A\) est un majorant de \((x_n)\) si \(x_n\leq A\) pour tout \(n\in\mathbb{R}\). Une suite qui possède un majorant est dite majorée.

Soit \(A\in\mathbb{R}\) et \((x_n)\) une suite, on dit que \(A\) est un minorant de \((x_n)\) si \(x_n\geq A\) pour tout \(n\in\mathbb{R}\). Une suite qui possède un majorant est dite minorée.

Une suite est bornée si elle est à la fois majorée et minorée.

Exemple 1.2 Une suite \((x_n)\) est constante s’il existe \(a\in\mathbb{R}\) tel que \(x_n=a\) pour tout \(n\in\mathbb{N}\). Une suite constante est toujours convergente de limite égale à la constante \(a\).

Exemple 1.3 La suite \((1/n)_{n\in\mathbb{N}^*}\) converge vers 0.

Preuve. Fixons \(\varepsilon>0\) alors \(1/\varepsilon>0\) et il existe \(N\in\mathbb{N}^*\) tel que \(N\geq 1/\varepsilon\). Maintenant, pour \(n\geq N\), \(0\leq\frac{1}{n}\leq\frac{1}{N}\leq \varepsilon\) et donc \(\left|\frac{1}{n}-0\right|\leq\varepsilon\) et on a bien montré que \(\lim \frac{1}{n}=0\).

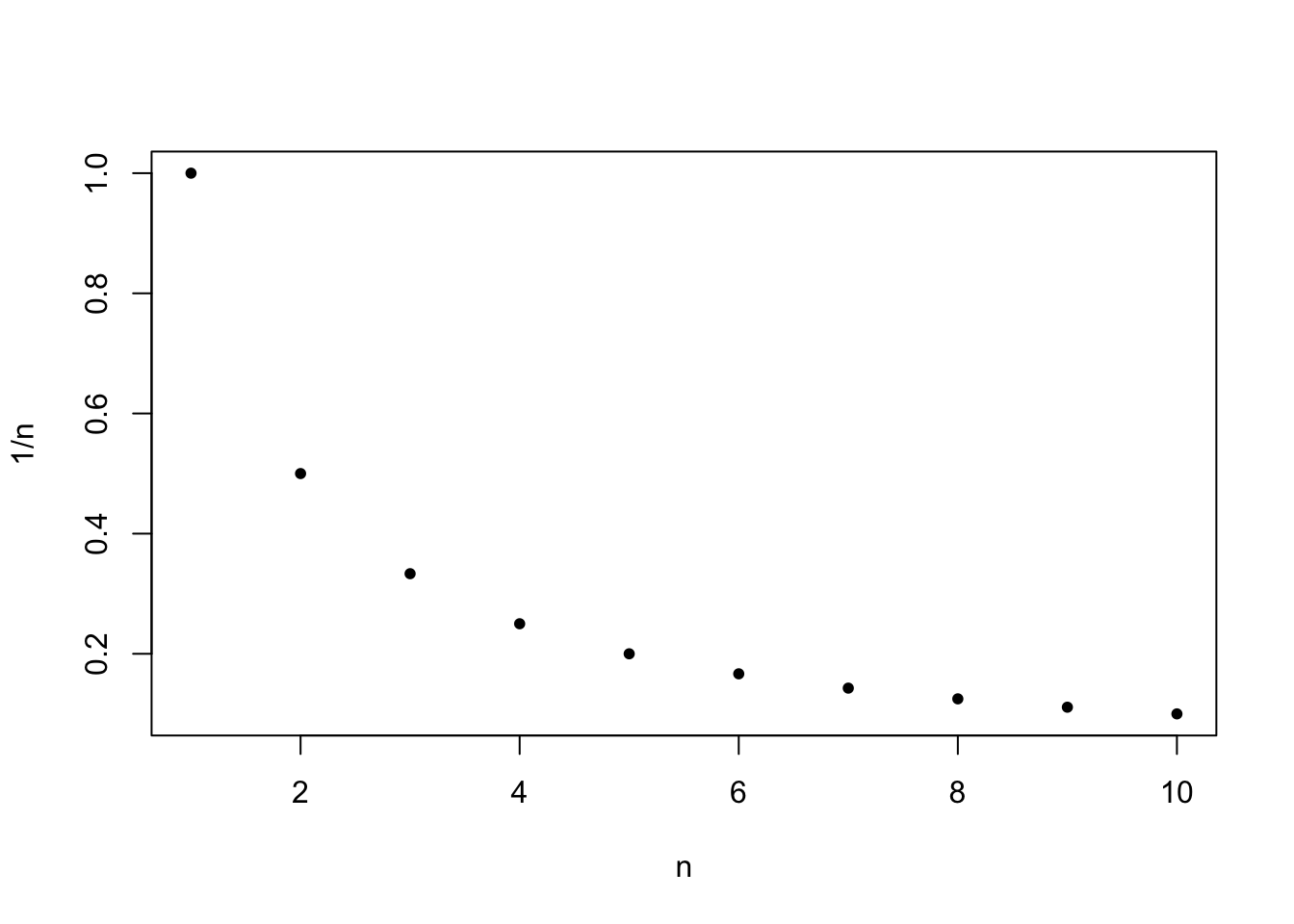
Figure 1.2: Les premières valeurs de la suite de terme général \(x_n=1/n\) qui converge vers 0.

1.3 Opérations sur les limites

Proposition 1.1 Soit \((x_n)\) et \((y_n)\) deux suites convergentes de limites respectives \(\ell_1\) et \(\ell_2\).

La suite \(x_n+y_n\) est convergente avec \(\lim x_n+y_n=\ell_1+\ell_2\).
La suite \(x_ny_n\) est convergente avec \(\lim x_ny_n=\ell_1\ell_2\).
Si \(\ell_2\neq0\) et \(y_n\neq 0\) pour tout \(n\in\mathbb{N}\) alors la suite \(x_n/y_n\) est convergente avec \(\lim x_n/y_n=\ell_1/\ell_2\).
Si \(x_n\leq y_n\) pour tout \(n\in\mathbb{N}\) alors \(\ell_1\leq \ell_2\).

Preuve. On montre les propriétés dans l’ordre.

Soit \(\varepsilon>0\). Comme \(x_n\to\ell_1\), il existe \(N_1\) tel que pour tout \(n\geq N_1\), \(|x_n-\ell_1|\leq \varepsilon/2\). De même, il \(N_1\) tel que pour tout \(n\geq N_2\), \(|y_n-\ell_2|\leq \varepsilon/2\). Maintenant pour \(n\geq\max\{N_1,N_2\}\), \(|x_n+y_n-(\ell_1+\ell_2)|=|x_n-\ell_1+ y_n-\ell_2|\leq |x_n-\ell_1|+|y_n-\ell_2|\leq \varepsilon/2+\varepsilon/2=\varepsilon\).
Soit \(\varepsilon>0\). Soit \(A\) un majorant strictement positif de \((|x_n|)\) (qui existe, car toute suite convergente est bornée, voir l’Exercice 1.3). On a

\[\begin{align} |x_ny_n-\ell_1\ell_2|&=|x_ny_n-x_n\ell_2+x_n\ell_2-\ell_1\ell_2|\\ &\leq|x_ny_n-x_n\ell_2|+|x_n\ell_2-\ell_1\ell_2|\\ &\leq|x_n||y_n-\ell_2|+|\ell_2||x_n-\ell_1|\\ &\leq A|y_n-\ell_2|+|\ell_2||x_n-\ell_1| \end{align}\]

On choisit \(N_1\) tel que pour tout \(n\geq N_1\), \(|x_n-\ell_1|\leq \varepsilon/2|\ell_2|\) et \(N_2\) tel que pour tout \(n\geq N_2\), \(|y_n-\ell_2|\leq \varepsilon/2A\). Ainsi, pour \(n\geq \max\{N_1,N_2\}\), on a \[ A|y_n-\ell_2|+|\ell_2||x_n-\ell_1|\leq \varepsilon\] et donc \(|x_ny_n-\ell_1\ell_2|\leq \varepsilon\). Ce qui montre que \(x_ny_n\) converge \(\ell_1\ell_2\).

Montrons d’abord le cas particulier où \((x_n)\) est constante égale à 1, c’est-à-dire montrons que \(1/y_n\to1/\ell_2\). On a

\[\left|\frac{1}{y_n}-\frac{1}{\ell_2}\right|=\left|\frac{\ell_2-y_n}{y_n\ell_2}\right|\]

Comme \(y_n\to\ell_2\), il existe \(N\in\mathbb{N}\) tel que pour tout \(n\geq N\), \(|y_n|\geq |\ell_2|/2\). Ainsi \(\left|\frac{1}{y_n}-\frac{1}{\ell_2}\right|\leq \frac{2}{|\ell_2|^2} |y_n-\ell_2|\) et donc pour \(n\) assez grand pour que \(|y_n-\ell_2|\leq\varepsilon/(2/|\ell_2|^2)\), on a bien \(\left|\frac{1}{y_n}-\frac{1}{\ell_2}\right|\leq\varepsilon\).

Dans le cas général, on utilise le fait que \(\frac{x_n}{y_n}=x_n\cdot \frac{1}{y_n}\) et on utilise les résultats précédents avec \(x_n\to\ell_1\) et \(1/y_n\to1/\ell_2\).

Supposons par l’absurde que \(\ell_1>\ell_2\). Posons \(\varepsilon=\frac{\ell_1-\ell_2}{3}\), alors il existe \(N_1\in\mathbb{N}\) tel que pour tout \(n\geq N_1\), \(x_n\geq\ell_1-\varepsilon\) et \(N_2\in\mathbb{N}\) tel que pour tout \(n\geq N_2\), \(y_n\leq \ell_2+\varepsilon\). Ainsi,

\[\ell_1-\varepsilon\leq x_n\leq y_n\leq\ell_2+\varepsilon\] et donc \(\ell_1\leq \ell_2+2\varepsilon=\ell_2+2\frac{\ell_1-\ell_2}{3}=\ell_1-\varepsilon/3\). Ce qui est absurde.

Dans le cas particulier où l’une des suites est constante, on a les propriétés suivantes.

Proposition 1.2 On suppose que \((x_n)\) est une suite convergente de limite \(\ell\).

Pour tout \(a\in\mathbb{R}\), la suite de terme général \(x_n+a\) est convergente de limite \(\ell+a\).
Pour tout \(a\in\mathbb{R}\), la suite de terme général \(ax_n\) est convergente de limite \(a\ell\).
Si \(\ell\neq0\) et pour tout \(n\in\mathbb{N}\), \(x_n\neq0\) alors la suite de terme général \(a/x_n\) est convergente de limite \(a/\ell\).
Soit \(a\in\mathbb{R}\). Si \(x_n\geq a\) (respectivement \(x_n\leq a\)) pour tout \(n\in\mathbb{N}\) alors \(\ell_1\geq a\) (respectivement \(\ell_1\leq a\)).

1.4 Convergence monotone

Définition 1.5 (Bornes supérieures et inférieures) Si \((x_n)\) est une suite majorée, on note \(\sup x_n\) le plus petit des ses majorants.

Si \((x_n)\) est une suite minorée, on note \(\inf x_n\) le plus petit des ses minorants.

L’existence des ces bornes supérieures (\(\sup x_n\)) et inférieures (\(\inf x_n\)) n’est pas évidente et une conséquence d’une construction formelle de l’ensemble des nombres réels \(\mathbb{R}\). Nous ne rentrons pas dans ces détails et admettrons l’existence des bornes supérieures et inférieures. La construction donne la proposition suivante.

Proposition 1.3 Soit \((x_n)\) une suite majorée (respectivement minorée) de borne supérieure \(A=\sup x_n\) (respectivement borne inférieure \(A=\inf x_n\)) et \(\varepsilon>0\) . Alors il existe \(n\in\mathbb{N}\) tel que \(x_n\geq A-\varepsilon\) (respectivement \(x_n\leq A+\varepsilon\)).

Preuve. Soit \(\varepsilon>0\). S’il n’y avait pas de \(n\) tel que \(x_n\geq A-\varepsilon\) alors \(A-\varepsilon\) serait un majorant mais comme \(A-\varepsilon<A\), \(A\) ne serait pas le plus petit des majorants. Ce qui est absurde et donc on a bien l’existence de \(n\in\mathbb{N}\) tel que \(x_n\geq A-\varepsilon\).

Proposition 1.4 Toute suite \((x_n)\) croissante et majorée est convergente vers \(\sup x_n\). De même, toute suite \((x_n)\) décroissante et minorée est convergente vers \(\inf x_n\).

Preuve. La preuve est la même pour les deux énoncés en changeant ce qui doit l’être. On prouve seulement le premier et on note \(A=\sup x_n\). Soit \(\varepsilon>0\), par la Proposition 1.3, il existe \(n_0\in\mathbb{N}\) tel que \(x_{n_0}\geq A-\varepsilon\). Par croissance, on a aussi \(x_n\geq x_{n_0}\geq A-\varepsilon\) pour \(n\geq n_0\). Comme \(A\) est un majorant, on a aussi \(x_{n}\leq A\) pour tout \(n\in\mathbb{N}\) et donc \(n\in\mathbb{N}\).

Exemple 1.4 La suite \((x_n)\) définie par \(x_n=1/n\) pour \(n\in\mathbb{N}^*\) est décroissante et minorée par 0. On a déjà vu qu’elle converge vers 0 dans l’Exemple 1.3.

1.5 Limites infinies

Il existe des cas où une suite ne converge pas mais devient “aussi grande possible”. On dit qu’elle tend vers l’infini. La définition suivante rend rigoureuse cette notion.

Définition 1.6 Une suite \((x_n)\) converge vers \(+\infty\) si pour tout \(A>0\), il existe \(N\in\mathbb{N}\) tel que pour tout \(n\geq N\), \(x_n\geq A\). On note \(\lim x_n=+\infty\) ou \(x_n\to+\infty\).

Une suite \((x_n)\) converge vers \(-\infty\) si pour tout \(A<0\), il existe \(N\in\mathbb{N}\) tel que pour tout \(n\geq N\), \(x_n\leq A\). On note \(\lim x_n=-\infty\) ou \(x_n\to-\infty\).

Remarque. On fera attention au fait qu’une suite convergente (au sens de la Définition 1.3) converge vers une limite finie. Une suite qui converge vers \(\pm\infty\) n’est pas convergente.

Exemple 1.5 Pour un entier strictement positif \(k\), la suite \((x_n)\) où \(x_n=n^k\) converge vers \(+\infty\). Si \(k=2\), c’est la suite des carrés : \(1,4,9,16,25,36,49,64,81,100,121,144\dots\)

Preuve. Soit \(A>0\), on choisit un entier \(N\geq A\) et \(N\geq1\), par exemple, \(N=\lfloor A\rfloor+1\) (partie entière plus 1). Pour \(n\geq N\), on a \(n^k=\underbrace{n\times\cdots\times n}_{k\ \textrm{fois}}\geq n\geq N\geq A\) car \(n\geq 1\) et \(k\geq 1\).

Proposition 1.5 Une suite croissante non majorée converge vers \(+\infty\). De même, une suite décroissante non minorée converge vers \(-\infty\).

Preuve. On prouve uniquement le cas d’une suite croissante, la preuve s’adapte pour le cas décroissant. Soit \((x_n)\) une suite croissante non majorée. Soit \(A>0\). Comme la suite n’est pas pas majorée, \(A\) n’est pas un majorant et donc il existe \(n_0\in\mathbb{N}\) tel que \(x_{n_0}>A\) et donc par croissance, pour tout \(n\geq n_0\), \(x_n\geq x_{n_0}\geq A\). Ce qui montre bien que \(\lim x_n=+\infty\).

Proposition 1.6 Soit \((x_n)\) et \((y_n)\) avec \(x_n\leq y_n\) pour tout \(n\in\mathbb{N}\).

Si \(\lim x_n=+\infty\) alors \(\lim y_n=+\infty\).
Si \(\lim y_n=-\infty\) alors \(\lim x_n=-\infty\).

Preuve. Supposons \(\lim x_n=+\infty\) et choisissons \(A>0\) alors il existe \(N\in\mathbb{N}\) tel que pour tout \(n\geq N\) \(x_n\geq A\). Ainsi, pour \(n\geq N\), \(y_n\geq x_n\geq A\) et on a prouvé que \(\lim y_n=+\infty\).

Le second cas se traite de manière analogue.

Proposition 1.7 Soit \((x_n)\) une suite telle que \(x_n\to\pm\infty\) alors \(1/x_n\to 0\).

Preuve. Soit \(\varepsilon>0\). Il existe \(N\in\mathbb{N}\) tel que pour tout \(n\geq N\), \(|x_n|\geq 1/\varepsilon\) donc pour \(n\geq N\), \(|0-1/x_n|=|1/x_n|\leq \varepsilon\).

Proposition 1.8 Soit \((x_n)\) et \((y_n)\) deux suites

Si \(\lim x_n=a\in\mathbb{R}\) et \(\lim y_n=+\infty\) alors \(\lim x_n+y_n=+\infty\). Si \(a>0\), \(\lim x_ny_n=+\infty\) et si \(a<0\) alors \(\lim x_ny_n=-\infty\).
Si \(\lim x_n=a\in\mathbb{R}\) et \(\lim y_n=-\infty\) alors \(\lim x_n+y_n=-\infty\). Si \(a>0\), \(\lim x_ny_n=-\infty\) et si \(a<0\) alors \(\lim x_ny_n=+\infty\).

Preuve. On traite seulement le premier cas puisque le second est analogue. Comme la suite \((x_n)\) est convergente, elle est bornée. Soit \(C\) un majorant de \((|x_n|)\). Soit \(A>0\), il existe \(N\in\mathbb{N}\) tel que pour tout \(n\geq N\), \(y_n\geq A+C\) et ainsi, \(x_n+y_n\geq -C+A+C=A\) et donc \(x_n+y_n\to+\infty\).

On suppose \(a>0\) et fixons \(A>0\). Comme \(x_n\to a\), il existe \(N\in\mathbb{N}\) tel que pour tout \(n\geq N\), \(|x_n-a|\leq a/2\) et donc \(x_n\geq a/2\). Comme \(y_n\to\infty\), il existe \(N_2\in\mathbb{N}\) tel que pour tout \(n\geq N_2\), \(y_n\geq 2A/a\) et ainsi \(x_ny_n\geq \frac{2A}{a}\frac{a}{2}=A\). Ce que l’on voulait montrer.

On suppose maintenant \(a<0\) et fixons \(A<0\). Comme \(x_n\to a\), il existe \(N\in\mathbb{N}\) tel que pour tout \(n\geq N\), \(|x_n-a|\leq a/2\) et donc \(x_n\leq a/2<0\). Comme \(y_n\to\infty\), il existe \(N_2\in\mathbb{N}\) tel que pour tout \(n\geq N_2\), \(y_n\geq 2A/|a|\) et ainsi \(x_ny_n\leq \frac{2A}{a}\frac{a}{2}=A\). Ce que l’on voulait montrer.

1.6 Suites arithmétiques et géométriques

1.6.1 Suites arithmétiques

Théorème 1.1 Soit \((x_n)\) une suite arithmétique de raison \(r\).

Si \(r>0\) alors \(\lim x_n=+\infty\).
Si \(r=0\) alors \(\lim x_n=x_0\).
Si \(r<0\) alors \(\lim x_n=-\infty\).

Preuve. Un raisonnement par récurrence montre que \(x_n=x_0+nr\).

Si \(r>0\) alors pour \(A>0\) fixé, on prend \(N=\lfloor (A-x_0)/r\rfloor+1\) (partie entière de \(A-x_0\) +1) et alors pour \(n\geq N\), \(n\geq (A-x_0)/r\), ce qui donne \(x_n=x_0+nr\geq A\) et donc \(\lim x_n=+\infty\).
Si \(r=0\) alors la suite \((x_n)\) est constante égale à \(x_0\) et converge donc vers cette limite.
Si \(r<0\) alors pour \(A<0\) fixé, on prend \(N\) entier plus grand que \((A-x_0)/r\) (remarquons que \(A/r>0\) car \(A\) et \(r\) sont négatifs). Maintenant, pour \(n\geq N\), \[n\geq \frac{A-x_0}{r}\] et comme \(r<0\),

\[nr\leq A-x_0\] et donc \(x_n=x_0+nr\leq A\). Ainsi, \(\lim x_n=-\infty\).

1.6.2 Suites géométriques

Commençons avec un petit lemme qui permettra de comparer suites géométriques et arithmétiques.

Lemme 1.4 (Inégalité de Bernoulli) Pour tout réel \(a\geq0\) et nombre entier \(n\in\mathbb{N}\), on a

\[(1+a)^n\geq1+na.\]

Preuve. On le montre par récurrence sur \(n\). Pour \(n=0\), on obtient \(1=1\) et la récurrence est initialisée. Supposons maintenant le résultat pour \(n\) fixé. Alors \((1+a)^{n+1}=(1+a)^n\cdot(1+a)\geq(1+na)(1+a)=1+(n+1)a+na^2\geq 1+(n+1)a\). Ce qui montre l’étape de récurrence.

Dans le théorème suivant, on se place dans le cas d’une suite géométrique de premier terme \(x_0\) non nul. En effet, si \(x_0=0\), la suite est constante égale à 0 et il n’y a rien de plus à dire.

Théorème 1.2 Soit \((x_n)\) une suite géométrique de raison \(r\) avec \(x_0\neq0\).

Si \(r>1\) alors \(\lim x_n=+\infty\) si \(x_0>0\) et \(\lim x_n=-\infty\) si \(x_0<0\).
Si \(r=1\) alors la suite est constante égale à \(x_0\).
Si \(|r|<1\) alors \(\lim x_n=0\).
Si \(r\leq -1\) alors la suite \((x_n)\) n’est pas convergente.

Preuve. Un raisonnement par récurrence montre que \(x_n= r^nx_0\).

Si \(r>1\) alors posons \(a=r-1>0\). Ainsi, \(r^n=(1+a)^n\geq 1+na\). Pour \(A>0\), on choisit \(N\) entier supérieur à \(A/a\), ainsi pour \(n\geq N\), \(n\geq A/a\) et donc \(r^n\geq A\). Ce qui montre que \(r^n\to+\infty\) et donc \(x_n\to+\infty\).
Si \(r=1\) alors \(r^n=1\) pour tout \(n\) et donc \(x_n=x_0\) pour tout \(n\).
Si \(|r|<1\) alors \(1/|r|>1\) et donc par le premier cas, pour tout \(\varepsilon>0\), il existe \(N\in\mathbb{N}\) tel que pour tout \(n\geq N\), \(\left(1/|r|\right)^n\geq \frac{|x_0|}{\varepsilon}\) et ainsi \(|r^nx_0|\leq\varepsilon\). Ce qui montre que \(x_n=r^nx_0\to0\).
Si \(r< -1\) alors \(|x_n|=|r|^n|x_0|\to\infty\) car \(|r|>1\). Ainsi, la suite n’est pas bornée et donc ne peut pas converger (voir l’Exercice 1.3)
Si \(r=-1\) alors on se retrouve dans une situation analogue au point 1. de l’Exercice 1.4 et la suite ne converge pas.

1.7 Suites adjacentes

Définition 1.7 Soit \((x_n)\) et \((y_n)\) deux suites numériques. On dit que ces suites sont adjacentes si \(x_n\leq y_n\) pour tout \(n\in\mathbb{N}\), \((x_n)\) est croissante, \((y_n)\) est décroissante et \(\lim y_n-x_n=0\).

Théorème 1.3 (Théorème des suites adjacentes) Si \((x_n)\) et \((y_n)\) sont deux suites adjacentes alors ces deux suites sont convergentes et \(\lim x_n=\lim y_n\).

Preuve. La suite \((x_n)\) est croissante majorée (par \(y_0\) par exemple) et donc converge vers une limite \(\ell_1\). De même, \((y_n)\) est décroissante minorée et donc converge vers une limite \(\ell_2\). Ainsi la suite \((y_n-x_n)\) est convergente de limite \(\ell_2-\ell_1\). Comme \(\lim y_n-x_n=0\), on a \(\ell_2-\ell_1=0\) et donc \(\ell_1=\ell_2\).

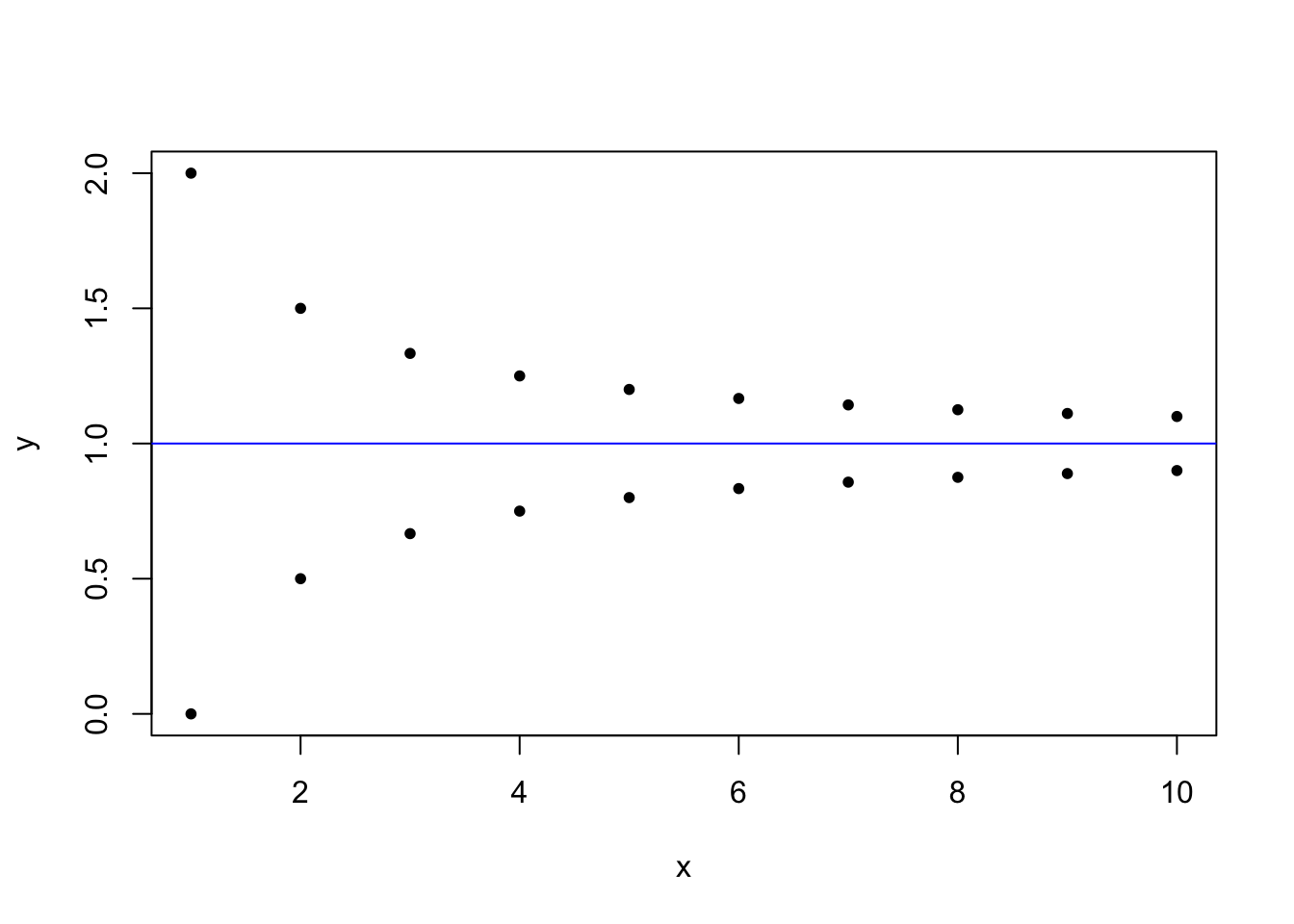
Figure 1.3: Deux suites adjacentes qui convergent vers 1.

Théorème 1.4 (Théorème des gendarmes) Soit \((x_n), (y_n)\) et \((u_n)\) trois suites telles que pour tout \(n\in\mathbb{N}\), \(x_n\leq u_n\leq y_n\) et telles \((x_n), (y_n)\) sont convergentes avec \(\lim x_n=\lim y_n=\ell\) alors \((u_n)\) est convergente de limite \(\ell\).

Preuve. On fixe \(\varepsilon>0\). Comme \(x_n\to\ell\) et \(y_n\to\ell\), il existe \(N\in\mathbb{N}\) tel que pour tout \(n\geq N\), \(x_n\geq \ell-\varepsilon\) et \(y_n\leq \ell+\varepsilon\).

Ainsi, \(\ell-\varepsilon\leq u_n\geq\ell+\varepsilon\) et donc \(|u_n-\ell|\leq\varepsilon\).

1.8 Exercices

Exercice 1.1 Donner un exemple d’une suite qui n’est pas monotone.

Exercice 1.2 Montrer qu’une suite \((x_n)\) est bornée si et seulement s’il existe \(A\geq 0\) tel que pour tout \(n\in \mathbb{N}\), \(|x_n|\leq A\).

Exercice 1.3 Montrer qu’une suite convergente est toujours bornée.

Exercice 1.4 Indiquer si les suites de termes généraux indiqués ci-dessous sont croissantes, décroissantes, minorées, majorées, bornées, convergentes ou admettent des limites infinies.

\(a_n=(-1)^n\)
\(b_n=\frac{(-1)^n}{n}\)
\(c_n=\sqrt{n}\)
\(d_n=(-1)^nn\)
\(e_n=n^2+1/n\)

Exercice 1.5 On définit deux suites \((x_n)\) et \((y_n)\) par \(x_n=2^n\) et \(y_n=3^n\). Déterminer le comportement des suites de termes généraux \(z_n=x_n+y_n\), \(u_n=x_n-y_n\), \(v_n=x_ny_n\), \(w_n=x_n/y_n\) et \(t_n=y_n/x_n\).

Exercice 1.6 Soit \((x_n)\) une suite convergente de limite \(\ell\). On pose \(y_n=x_{2n}\) pour tout \(n\in\mathbb{N}\). Montrer que la suite \((y_n)\) est convergente de limite \(\ell\).

Exercice 1.7 Soit \(a,b\in \mathbb{R}\). On fixe \(x_0\) et on définit récursivement \(x_{n+1}=ax_n+b\).

Déterminer le comportement de \((x_n)\) si \(a=0\) ou \(a=1\).
On suppose \(a\neq0\) et \(a\neq1\). On pose \(c=\frac{b}{a-1}\) et \(y_n=x_n+c\). Montrer que \((y_n)\) est une suite géométrique de raison \(a\).
En fonction de \(a\), déterminer le comportement de \(y_n\) puis celui de \(x_n\).
À l’aide de la formule explicite d’une suite géométrique, déduire une formule explicite pour \(x_n\).