Chapitre 2 Continuité et dérivabilité des fonctions

Définition 2.1 Un intervalle est une partie \(I\subset\mathbb{R}\) telle que pour tout \(x,y\in I\), si \(z\geq x\) et \(z\leq y\) alors \(z\in I\).

Il y a de différents types d’intervalles:

Pour \(a\geq b\), \([a,b]=\{x\in\mathbb{R},\ a\leq x\ \mathrm{et}\ x\leq b\}\) est un intervalle fermé ou encore un segment.
Pour \(a\geq b\), \([a,b[=\{x\in\mathbb{R},\ a\leq x\ \mathrm{et}\ x< b\}\) est un intervalle fermé en \(a\), ouvert en \(b\).
Pour \(a\geq b\), \(]a,b]=\{x\in\mathbb{R},\ a< x\ \mathrm{et}\ x< b\}\) est un intervalle ouvert en \(a\), fermé en \(b\).
Pour \(a\geq b\), \(]a,b[=\{x\in\mathbb{R},\ a\leq x\ \mathrm{et}\ x< b\}\) est un intervalle ouvert.
Pour \(a\in\mathbb{R}\), \(]-\infty,a]=\{x\in\mathbb{R},\ x\leq a\}\) est un intervalle infini fermé en \(a\).
Pour \(a\in\mathbb{R}\), \(]-\infty,a[=\{x\in\mathbb{R},\ x< a\}\) est un intervalle infini ouvert en \(a\).
Pour \(a\in\mathbb{R}\), \([a,+\infty[=\{x\in\mathbb{R}, \ x\geq a\}\) est un intervalle infini fermé en \(a\).
Pour \(a\in\mathbb{R}\), \(]a,+\infty[=\{x\in\mathbb{R}, \ x> a\}\) est un intervalle infini ouvert en \(a\).
\(]-\infty,+\infty[=\mathbb{R}\)

Remarque. Si \(a>b\) on définira \([a,b]\) comme étant \([b,a]\) et de même pour les autres types d’intervalles. Cela sera particulièrement utile si on ne sait pas qui de \(a\) ou \(b\) est le plus grand. Les nombres \(a,b\) (éventuellement égaux à \(\pm\infty\)) sont les bornes de l’intervalle.

2.1 Limite de fonctions réelles

Définition 2.2 Soit \(I\) un intervalle, \(f\colon I\to \mathbb{R}\) une fonction et \(a\in I\) ou une borne de \(I\). On dit que \(f\) a une limite \(\ell\) en \(a\) si pour tout \(\varepsilon>0\), il existe \(\delta>0\) tel que pour tout \(x\in I\)

\[|x-a|\leq \delta\implies |f(x)-\ell|\leq\varepsilon.\] On notera \(\lim f(x)=\ell\) quand \(x\to a\).

Définition 2.3 (limite infinie) Soit \(I\) un intervalle, \(f\colon I\to \mathbb{R}\) une fonction et \(a\in I\) ou une borne de \(I\). On dit que \(f\) a pour limite \(+\infty\) (respectivement \(-\infty\)) en \(a\) si pour tout \(A>0\) (respectivement \(A<0\)), il existe \(\delta>0\) tel que pour tout \(x\in I\),

\[|x-a|\leq \delta\implies f(x)\geq A\ (\textrm{respectivement}\ f(x)\leq A).\] On notera \(\lim f(x)=+\infty\) (respectivement \(\lim f(x)=-\infty\)) quand \(x\to a\).

Définition 2.4 (limite en l'infini) Soit \(I\) un intervalle de la forme \([a,+\infty[\) (respectivement \(]-\infty,a]\)) et \(f\colon I\to \mathbb{R}\) une fonction. On dit que \(f\) a une limite \(\ell\) en \(+\infty\) (respectivement \(-\infty\)) si pour tout \(\varepsilon>0\), il existe \(A>0\) (respectivement \(A<0\)) tel que pour tout \(x\in I\)

\[x\geq A\ (\textrm{respectivement}\ x\leq A)\implies |f(x)-\ell|\leq \varepsilon.\] On notera \(\lim f(x)=\ell\) quand \(x\to +\infty\) (respectivement \(x\to -\infty\)).

Définition 2.5 (limite infini en l'infini) Soit \(I\) un intervalle de la forme \([a,+\infty[\) et \(f\colon I\to \mathbb{R}\) une fonction. On dit que \(f\) a pour limite \(+\infty\) (respectivement \(-\infty\)) en \(+\infty\) si pour tout \(A>0\) (respectivement \(A<0\)), il existe \(B>0\) tel que pour tout \(x\in I\),

\[x\geq B\ \implies f(x)>A\ (\textrm{respectivement}\ f(x)<A).\] On notera \(\lim f(x)=+\infty\) (respectivement \(\lim f(x)=-\infty\)) quand \(x\to+\infty\).

Soit \(I\) un intervalle de la forme \(]-\infty,a]\) et \(f\colon I\to \mathbb{R}\) une fonction. On dit que \(f\) a pour limite \(+\infty\) (respectivement \(-\infty\)) en \(-\infty\) si pour tout \(A>0\) (respectivement \(A<0\)), il existe \(B<0\) tel que pour tout \(x\in I\),

\[x\leq B\ \implies f(x)>A\ (\textrm{respectivement}\ f(x)<A).\] On notera \(\lim f(x)=+\infty\) (respectivement \(\lim f(x)=-\infty\)) quand \(x\to-\infty\).

2.2 Continuité de fonctions réelles

Définition 2.6 Soit \(I\) un intervalle. Une fonction \(f\colon I\to\mathbb{R}\) est continue en un point \(a\in I\) si pour tout \(\varepsilon>0\) il existe \(\delta>0\) tel que pour tout \(x\in I\), si \(|x-a|\leq \delta\) alors \(|f(x)-f(a)|\leq \varepsilon\).

Une fonction \(f\colon I\to\mathbb{R}\) est continue si elle est continue en chaque \(a\in I\).

Remarque. De manière imagée, une fonction continue sur un intervalle \(I\) est une fonction dont on peut tracer le graphe sans lever le stylo.

La définition signifie exactement que \(f\) a une limite en \(a\) qui est \(f(a)\).

Exemple 2.1 Voici quelques exemples.

Une fonction constante est continue. Pour tout \(\varepsilon>0\) et tout point \(x\), on peut prendre \(\delta=1\) par exemple pour satisfaire la définition.
La fonction identité de \(\mathbb{R}\to\mathbb{R}\) donnée par \(f(x)=x\) est continue en chaque point. Il suffit de prendre \(\delta=\varepsilon\) dans la définition.
La fonction \(f\colon \mathbb{R}\to\mathbb{R}\) donnée par \(f(x)=1\) si \(x\geq0\) et \(f(x)=0\) si \(x<0\) est continue sur \(]-\infty,0[\) et sur \(]0;+\infty[\) mais pas continue en \(0\) car on peut rendre \(|x|\) aussi petit que voulu avec \(x<0\) mais on a toujours \(|f(x)-f(0)|=1\) et pour \(\varepsilon=1/2\) par exemple la définition n’est pas satisfaite.

Proposition 2.1 Soit \(I\) un intervalle. Une fonction \(f\colon I\to\mathbb{R}\) est continue en un point \(a\in I\) si et seulement si pour toute suite \((x_n)_{n\in\mathbb{N}}\) de points de \(I\) tels que \(x_n\to a\), la suite \((f(x_n))\) converge vers \(f(x)\).

Preuve. On suppose \(f\) continue en \(a\) et \((x_n)\) une suite de points de \(I\) avec \(x_n\to a\). Alors pour \(\varepsilon>0\), il existe \(\delta>0\) tel que pour \(|x-a|\leq\delta\), \(|f(x)-f(a)|\leq \varepsilon\). Comme \(x_n\to a\), il existe \(N\) tel que pour tout \(n\geq N\), \(|x_n-a|\leq \delta\) et donc pour tout \(n\geq N\), \(|f(x_n)-f(a)|\leq \varepsilon\). Ce qui montre exactement que \((f(x_n))\to f(a)\).

Réciproquement, on suppose par l’absurde que \(f\) n’est pas continue en \(a\). Alors il existe \(\varepsilon>0\), tel que pour tout \(n\in \mathbb{N}\) différent de zéro, on peut trouver \(x_n\in I\) avec \(|x_n-a|\leq 1/n\) et \(|f(x_n)-f(a)|>\varepsilon\). En particulier, on a trouvé une suite \((x_n)\) avec \(x_n\to a\) et \((f(x_n))\) qui ne tend pas vers \(f(a)\).

En utilisant les opérations sur les suites, on a les résultats suivants.

Proposition 2.2 Soit \(I\) un intervalle et \(f,g\colon I\to \mathbb{R}\) deux fonctions.

La somme \(f+g\colon I\to\mathbb{R}\) est continue.
Le produit \(fg\colon I\to\mathbb{R}\) est continu.
Si \(g\) ne s’annule pas sur \(I\), le quotient \(f/g\colon I\to \mathbb{R}\) est continue.

Corollaire 2.1 Les fonctions polynomiales, c’est-à-dire les fonctions données par une formule du type \(f(x)=a_nx^n+a_{n+1}x^{n-1}+\dots a_1 x+a_0\) où les \(a_i\in\mathbb{R}\) sont des coefficients fixés, sont continues sur tout intervalle.

La fonction \(x\mapsto 1/x\) est continue sur \(]0,+\infty[\).

Proposition 2.3 Soit \(I,J\) deux intervalles, \(f\colon I\to \mathbb{R}\) et \(g\colon J\to \mathbb{R}\) deux fonctions continues telles que \(f(I)\subset J\). Alors la composée \(g\circ f\colon I\to \mathbb{R}\) est continue.

2.3 Propriétés globales des fonctions continues

Théorème 2.1 (Théorème des valeurs intermédiaires) Soit \(I\) un intervalle et \(f\colon I\to \mathbb{R}\) une fonction continue. Soit \(a,b\in I\) et \(y\in[f(a),f(b)]\) alors il existe \(c\in[a,b]\) tel que \(f(c)=y\).

Preuve. On procède par dichotomie. On se place dans le cas \(a<b\) et \(f(a)< f(b)\). Le cas \(f(a)=f(b)\) est évident, il suffit de prendre \(c=a\). le cas \(f(b)>f(a)\) se traite en adaptant facilement la preuve.

On définit deux suites de manière récursive avec \(x_0=a\) et \(y_0=b\). On suppose \(x_n\) et \(y_n\) définis.

Si \(f\left(\frac{x_n+y_n}{2}\right)\leq y\), on définit \(x_{n+1}=\frac{x_n+y_n}{2}\) et \(y_{n+1}=y_n\).
Si \(f\left(\frac{x_n+y_n}{2}\right)> y\), on définit \(x_{n+1}=x_n\) et \(y_{n+1}=\frac{x_n+y_n}{2}\).

Par construction, on a \((x_n)\) croissante, \((y_n)\) décroissante, \(x_n\leq y_n\) pour tout \(n\in\mathbb{N}\) et \(y_n-x_n=\frac{b-a}{2^n}\). Ainsi \(y_n-x_n\to 0\) et on peut appliquer le théorème des suites adjacentes aux suites \((x_n)\) et \((y_n)\) qui convergent vers une valeur commune \(c\). Comme \(a\leq x_n\leq y_n\leq b\), à la limite \(c\in[a,b]\). De plus, on a \(f(x_n)\leq y\leq f(y_n)\) et comme \(f(x_n)\to f(c)\) et \(f(y_n)\to f(c)\) par continuité de \(f\), on a \(f(c)\leq y\leq f(c)\) et donc \(f(c)=y\).

Remarque. Le théorème des valeurs intermédiaires est équivalent à dire que l’image d’un intervalle par une fonction continue est encore un intervalle.

Théorème 2.2 (Théorème des valeurs extrêmes) Une fonction continue sur un segment \(I\) est bornée et atteint ses bornes. Autrement dit, il existe \(a,b\in I\) tel que pour tout \(x\in I\),

\[f(a)\leq f(x)\leq f(b).\]

On peut prouver le résultat par dichotomie comme pour le théorème des valeurs intermédiaires.

Dans l’énoncé précédent \(f(a)\) est un minimum de \(f\) sur \(I\) et \(f(b)\) est un maximum de \(f\) sur \(I\). On appelle extremum une valeur de \(f\) qui est un maximum ou un minimum.

Théorème 2.3 (Théorème de la bijection continue) Soit \(a,b\in\mathbb{R}\) avec \(a<b\) et \(f\colon [a,b]\to[f(a),f(b)]\). Si \(f\) est continue sur \([a,b]\) et strictement croissante alors il existe une fonction continue strictement croissante \(g\colon [f(a),f(b)]\to [a,b]\) telle que pour tout \(x\in[a,b]\), \(g(f(x))=x\) et pour tout \(y\in[f(a),f(b)]\), \(f(g(y))=y\).

Similairement, si \(f\) est continue sur \([a,b]\) et strictement décroissante alors il existe une fonction continue strictement décroissante \(g\colon [f(b),f(a)]\to [a,b]\) telle que pour tout \(x\in[a,b]\), \(g(f(x))=x\) et pour tout \(y\in[f(a),f(b)]\), \(f(g(y))=y\).

Sous les hypothèses du théorème, on dit que \(f\) est inversible et que la fonction \(g\) est l’ inverse de \(f\). On dit aussi que \(g\) est la réciproque de \(f\) et on la note \(f^{-1}\).

Preuve. On prouve seulement le cas strictement croissant. La preuve de l’autre cas est similaire. Pour \(x<y\), on a \(f(x)<f(y)\) par stricte croissance donc la fonction \(f\) est injective. Pour tout \(y\in[a,b]\), il existe \(c\in[a,b]\) tel que \(f(c)=y\) par le théorème des valeurs intermédiaires (Théorème 2.1). La fonction \(f\) est donc surjective. Ainsi, \(f\colon[a,b]\to[f(a),f(b)]\) est bijective. Elle possède donc un inverse que l’on note \(f^{-1}\). Par stricte croissance de \(f\), on a \(x<y\iff f(x)<f(y)\) pour tout \(x,y\in[a,b]\). En appliquant cette équivalence à \(x=f^{-1}(x')\) et \(y=f^{-1}(y')\) pour \(x',y'\in[f(a),f(b)]\), on a \(f^{-1}(x')<f^{-1}(y')\iff x'<y'\), c’est-à-dire que \(f^{-1}\) est strictement croissante.

Exemple 2.2 La fonction \(x\mapsto x^2\) est continue strictement croissante sur \([0,+\infty[\). Le théorème précédent nous donne l’existence d’une fonction \(g\colon[0,+\infty[\to[0,+\infty[\) telle que pour \(x\geq 0\), \(g(x)^2=x.\) On vient de démontrer l’existence de la racine carrée \(\sqrt{x}\) pour \(x\geq0\).

2.4 Dérivation

Définition 2.7 Soit \(I\) un intervalle, \(f\colon I\to\mathbb{R}\) une fonction et \(a\in I\). On dit que \(f\) est dérivable en \(a\) s’il existe un nombre \(\lambda\in\mathbb{R}\) tel que pour tout \(\varepsilon>0\), il existe \(\delta>0\) tel que pour tout \(x\neq a\) dans \(I\),

\[\begin{equation} |x-a|<\delta \implies \left|\frac{f(x)-f(a)}{x-a}-\lambda\right|\leq\varepsilon. \tag{2.1} \end{equation}\]

La fonction \(f\) est dérivable sur \(I\) si elle est dérivable en tout point \(a\in I\).

Un tel nombre nombre \(\lambda\) comme dans la définition est unique et appelé nombre dérivé en \(a\). On le note \(f'(a)\). Si la fonction \(f\) est dérivable en tout point de l’intervalle \(I\). La fonction

\[ \begin{matrix} f' \colon& I&\to& \mathbb{R}\\ &x&\mapsto&f'(x) \end{matrix} \] est appelée la fonction dérivée de \(f\).

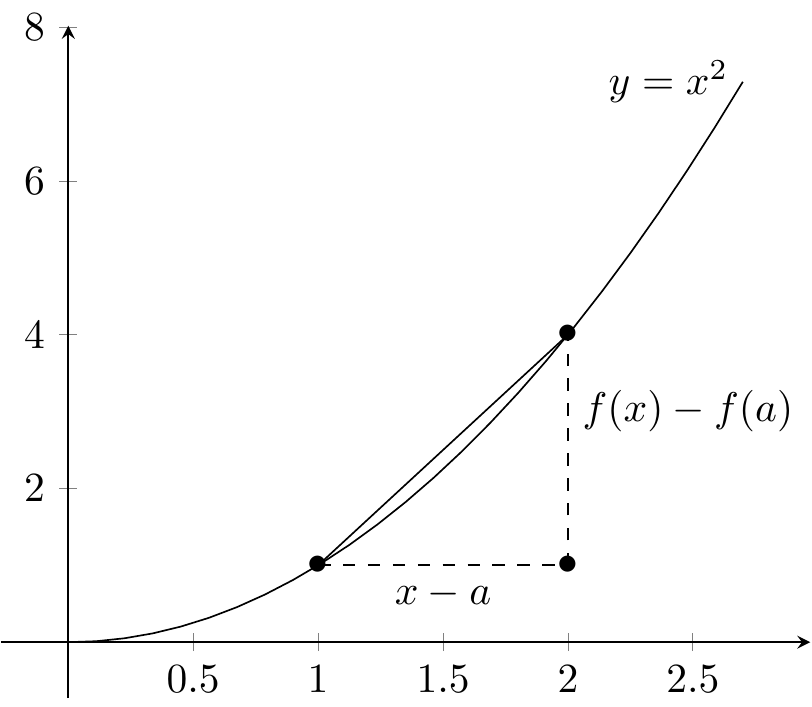
Figure 2.1: Le taux d’accroissement \((f(x)-f(a))/(x-a)\) correspond à la tangente de ce triangle.

Remarque. L’équation (2.1) est équivalente (quitte à prendre \(\delta\leq 1\)) à

\[|f(x)-\left(f(a)+(x-a)f'(a)\right)|\leq \varepsilon.\] Autrement dit \(f(x)\simeq f(a)+(x-a)f'(a)\). C’est-à-dire que proche de \(a\), on peut approcher la fonction \(f\) par une fonction affine, une fonction dont le graphe est une droite passant par \(f(a)\) et dont le coefficient directeur est \(f'(a)\).

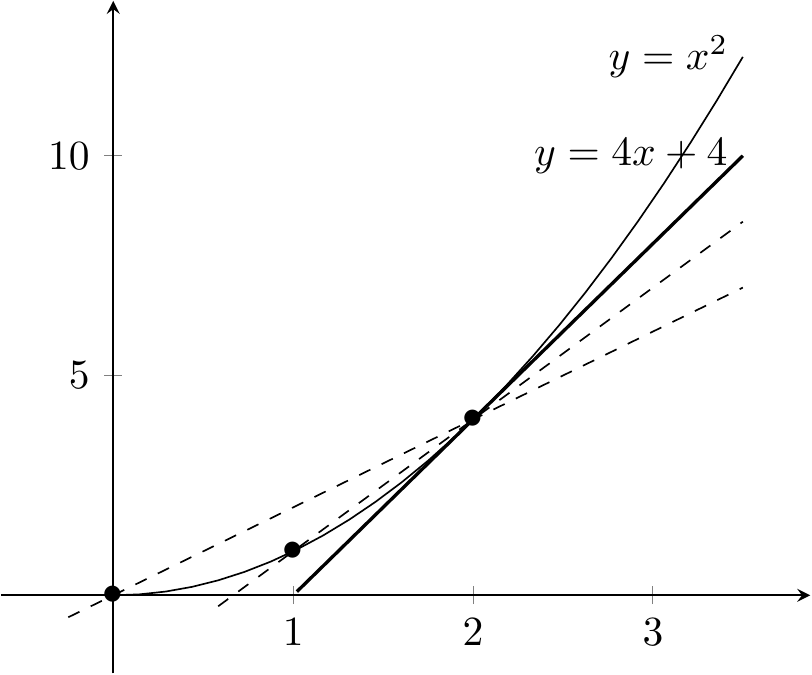
Figure 2.2: La tangente comme limite des cordes du graphe

Exemple 2.3 Voici quelques exemples de fonctions dérivables et non dérivables.

La dérivée d’une fonction constante est nulle puisque \(f(x)-f(a)=0\) pour tout \(x\in\mathbb{R}\).
La dérivée de la fonction identité \(x\mapsto x\) est constante égale à 1 puisque \(\frac{f(x)-f(a)}{x-a}=1\) pour tout \(x\neq a\).
Pour \(n\in\mathbb{N}\), la dérivée de la fonction \(x\mapsto x^n\) définie sur \(\mathbb{R}\) est \(x\mapsto nx^{n-1}\). En effet \[\begin{align*} \frac{x^n-a^n}{x-a}&=\frac{(x-a)(x^{n-1}+ax^{n-2}+a^2x^{n-3}+\dots+a^{n-2}x+a^{n-1})}{x-a}\\ &=x^{n-1}+ax^{n-2}+a^2x^{n-3}+\dots+a^{n-2}x+a^{n-1} \end{align*}\] et donc quand \(x\to a\), on obtient \(\frac{x^n-a^n}{x-a}\to na^{n-1}\).
La fonction \(f\colon\mathbb{R}\to\mathbb{R}\) donnée par \(f(x)=|x|\) est continue mais pas dérivable en \(0\). En effet, \(\frac{|x|-|0|}{x-0}=1\) si \(x>0\) et \(-1\) si \(x<0\).

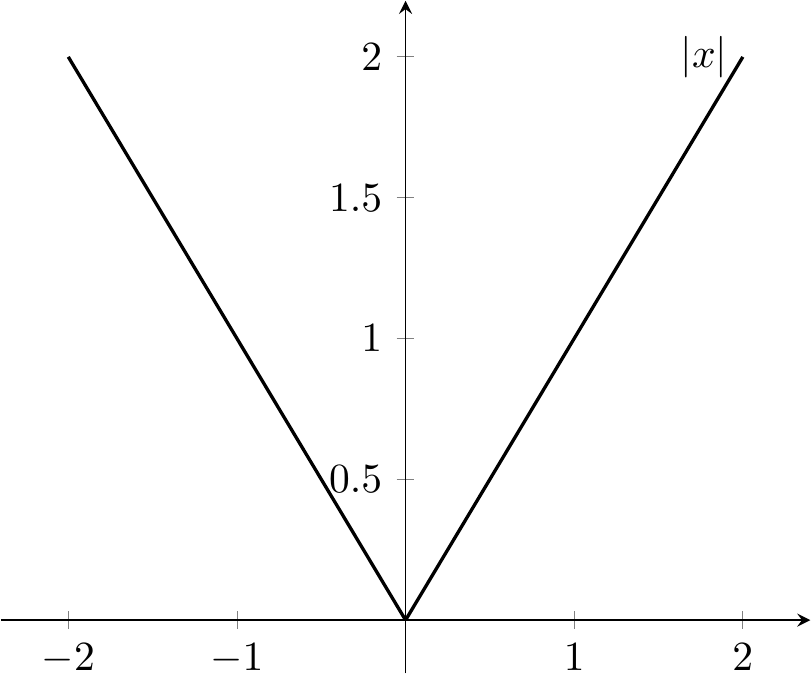
Figure 2.3: La fonction valeur absolue n’est pas dérivable en 0.

Lemme 2.1 Soit \(I\) un intervalle et \(f\colon I\to \mathbb{R}\). Si \(f\) est dérivable en \(a\in I\) alors \(f\) est continue en \(a\). Ainsi, si \(f\) est dérivable sur \(I\) alors \(f\) est continue sur \(I\).

Preuve. L’équation (2.1) donne \(|f(x)-f(a)|\leq \varepsilon|x-a|+|x-a||f'(a)|\) pour \(|x-a|\leq \delta\). Quitte à prendre \(\delta\) encore plus petit avec \(\delta\leq\max\left\{1/2,\frac{\varepsilon}{2|f'(a)|}\right\}\) (si \(f'(a)\neq0\)), on a \(|f(x)-f(a)|\leq \varepsilon\) pour \(|x-a|\leq \delta\). Ce qui montre que \(f\) est bien continue en \(a\).

Proposition 2.4 Soit \(I\) un intervalle et \(f,g\colon I\to\mathbb{R}\) deux fonctions dérivables sur \(I\).

La fonction somme \(f+g\) est dérivable sur I de dérivée \((f+g)'=f'+g'\)
La fonction produit \(fg\) (\(x\mapsto f(x)g(x)\)) est dérivable sur \(I\) de dérivée \((fg)'=f'g+fg'\).
Si \(g\) ne s’annule pas sur \(I\) alors la fonction quotient \(f/g\) est dérivable de dérivée \((f/g)'=\frac{f'g-fg'}{g^2}\).

Preuve. Pour la somme cela découle du fait

\[\frac{f(x)+g(x)-f(a)-g(a)}{x-a}=\frac{f(x)-f(a)}{x-a}+\frac{g(x)-g(a)}{x-a}\to f'(a)+g'(a)\] quand \(x\to a\).

Pour le produit, on écrit

\[\begin{align*} \frac{f(x)g(x)-f(a)g(a)}{x-a}&=\frac{f(x)g(x)-f(x)g(a)+f(x)g(a)-f(a)g(a)}{x-a}\\ &=f(x)\frac{g(x)-g(a)}{x-a}+g(a)\frac{f(x)-f(a)}{x-a}\\ &\to f(a)g'(a)+g(a)f'(a) \end{align*}\]

quand \(x\to a\).

Pour démontrer la formule de la dérivée d’un quotient, on peut d’abord démontrer la formule de la dérivée de \(x\mapsto 1/g(x)\) puis appliquer la formule de dérivation d’un produit. On a

\[\frac{1/g(x)-1/g(a)}{x-a}=\frac{1}{g(x)g(a)}\frac{g(a)-g(x)}{x-a}\to \frac{-g'(a)}{g(a)^2}\] quand \(x\to a\).

En écrivant \(fg\) comme le produit \(f\times \frac{1}{g}\), on obtient \((fg)'(x)=\frac{f'(x)}{g(x)}-\frac{f(x)g'(x)}{g(x)^2}\) et en mettant au même dénominateur, on obtient \(\left(\frac{f}{g}\right)'(x)=\frac{f'(x)g(x)-f(x)g'(x)}{g(x)^2}\).

Corollaire 2.2 Soit \(P\) le polynôme avec \(P(x)=\sum_{i=0}^n a_i x^i\). La fonction polynomiale associée \(x\mapsto P(x)\), notée aussi \(P\), est dérivable de dérivée \(P'(x)=\sum_{i=0}^{n-1}(i+1)a_{i+1}x^i\).

La fonction \(x\mapsto 1/x\) définie sur \(\mathbb{R}\setminus\{0\}\) est dérivable sur \(]0,+\infty[\) et \(]-\infty,0]\) de dérivée \(-1/x^2\).

Proposition 2.5 Soit \(I,J\) deux intervalles, \(f\colon I\to\mathbb{R}\) et \(g\colon J\to \mathbb{R}\) deux fonctions avec \(f(I)\subset J\). On suppose que \(f\) est dérivable en \(a\in I\) et \(g\) est dérivable en \(y=f(a)\). Alors la fonction \(g\circ f\colon I\to \mathbb{R}\) est dérivable en \(a\) et

\[(g\circ f)'(a)=g'(f(a))\cdot f'(a).\]

Preuve. On écrit

\[\frac{g(f(x))-g(f(a))}{x-a}=\frac{g(f(x))-g(f(a))}{f(x)-f(a)}\frac{f(x)-f(a)}{x-a}.\]

Comme \(g\) est dérivable en \(f(a)\) et \(f\) continue en \(a\), on a \(\frac{g(f(x))-g(f(a))}{f(x)-f(a)}\to g'(f(a))\) quand \(x\to a\) et comme \(f\) est dérivable en \(a\), on a \(\frac{f(x)-f(a)}{x-a}\to f'(a)\) quand \(x\to a\).

Ainsi,

\[ \frac{g(f(x))-g(f(a))}{x-a}\to g'(f(a))\cdot f'(a)\] quand \(x\to a\).

2.5 Accroissements finis

Proposition 2.6 Soit \(I\) un intervalle ouvert, \(f\colon I\to \mathbb{R}\) une fonction dérivable en \(a\in I\). Si \(f(a)\) est un extremum de \(f\) alors \(f'(a)=0.\)

Preuve. On prouve le résultat dans le cas où \(f(a)\) est un maximum. Le cas où \(f(a)\) est un minimum se traite de manière similaire en renversant les inégalités. Si \((x_n)\) est une suite de points tels que \(x_n\to a\) avec \(x_n<a\) alors \(f(x_n)\leq f(a)\) et donc \(\frac{f(x_n)-f(a)}{x_n-a}\geq 0\). Ainsi, \(f'(a)\geq0\). Si \((x_n)\) est une suite de points tels que \(x_n\to a\) avec \(x_n>a\) alors \(f(x_n)\leq f(a)\) et donc \(\frac{f(x_n)-f(a)}{x_n-a}\leq 0\). Ainsi, \(f'(a)\leq0\).

Au final \(f'(a)=0\).

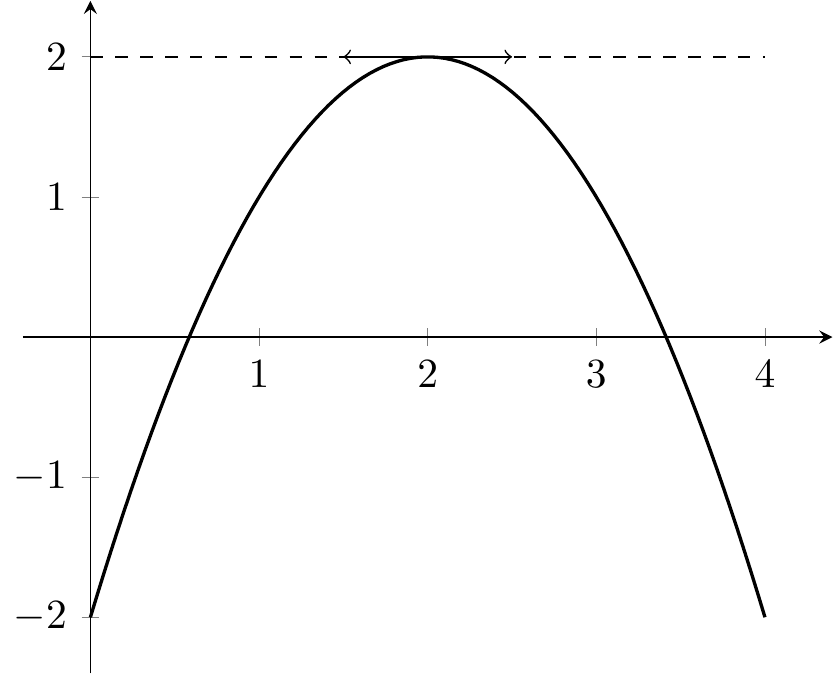
Figure 2.4: Une tangente horizontale en un maximum.

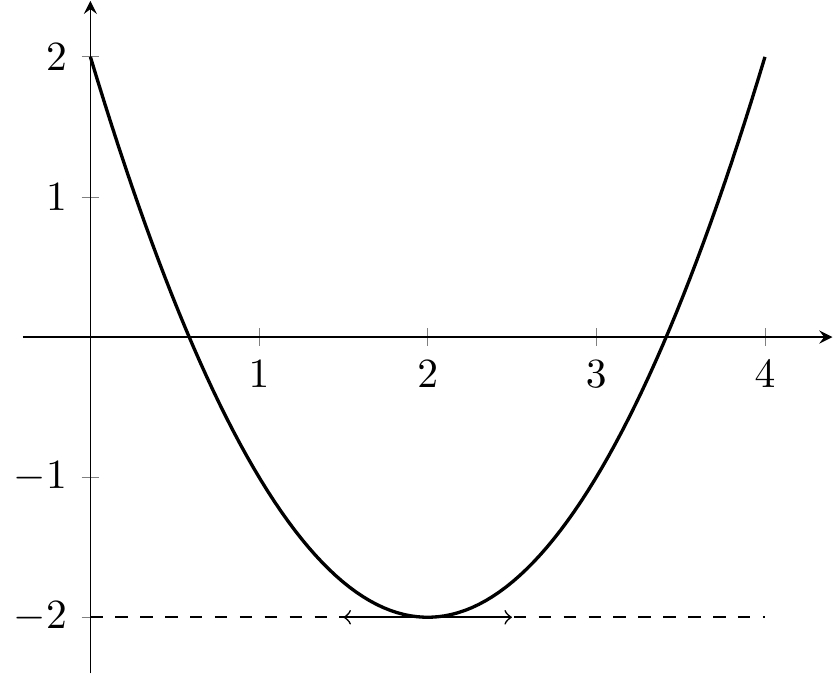
Figure 2.5: Une tangente horizontale en un minimum.

Remarque. Pour une fonction dérivable \(f\), il se peut que \(f'(x)=0\) sans que \(f(x)\) soit une valeur extrême.

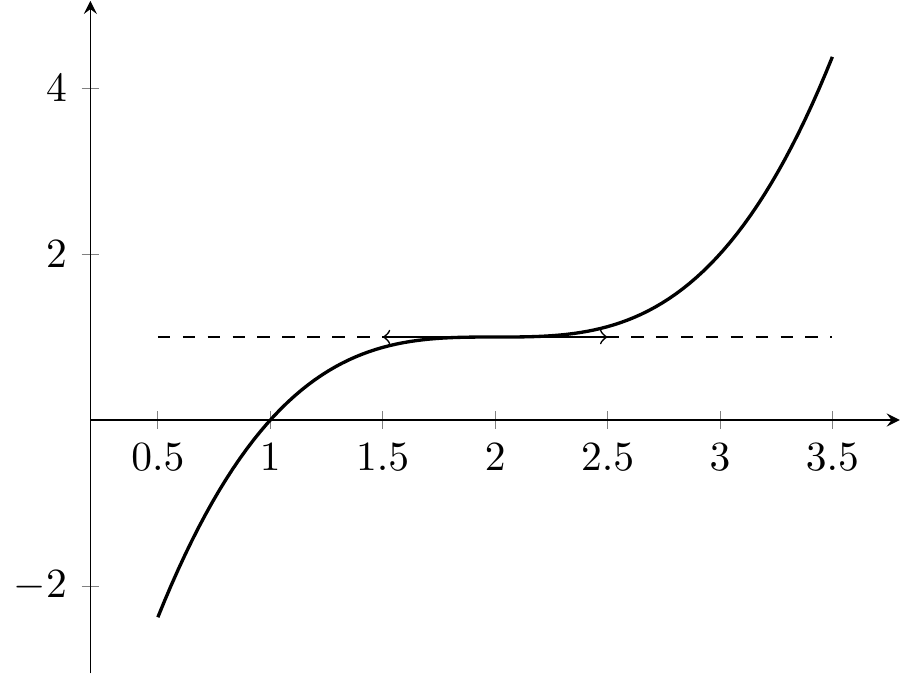
Figure 2.6: Une tangente horizontale sans extremum.

Théorème 2.4 (Théorème de Rolle) Soit \(a,b\in\mathbb{R}\) et \(f\colon[a,b]\to \mathbb{R}\) une fonction dérivable. Si \(f(a)=f(b)\) alors il existe \(c\in[a,b]\) tel que \(f'(c)=0\).

Preuve. Par le théorème des valeurs extrêmes (Théorème 2.2), il existe \(c\) tel que \(f(c)\) est une valeur extrême. Si \(f\) n’est pas constante (et dans ce cas, le résultat est évident), on peut supposer \(c\neq a,b\) et par la Proposition 2.6, \(f'(c)=0\).

Théorème 2.5 (Égalité des accroissements finis) Soit \(a<b\in\mathbb{R}\) et \(f\colon[a,b]\to\mathbb{R}\) une fonction dérivable. Alors, il existe \(c\in[a,b]\) tel que \(f'(c)=\frac{f(b)-f(a)}{b-a}\).

Preuve. On applique le théorème de Rolle à la fonction \(g(x)=f(x)-(x-a)\frac{f(b)-f(a)}{b-a}\) dont la dérivée est \(g'(x)=f'(x)-\frac{f(b)-f(a)}{b-a}\) et qui vérifie \(g(b)=f(a)\) et \(g(a)=f(a)\).

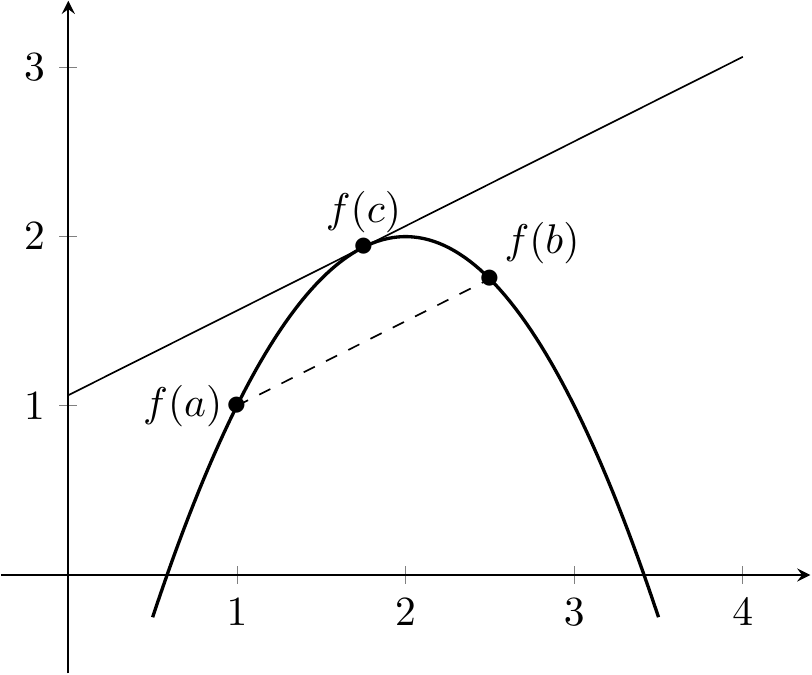
Figure 2.7: La tangente en \(c\) a une pente identique à la corde ici avec \(a=1\) et \(b=2,5\).

Théorème 2.6 (Inégalité des accroissements finis) Soit \(a<b\in\mathbb{R}\) et \(f\colon[a,b]\to\mathbb{R}\) une fonction dérivable. On suppose qu’il existe \(M\geq0\) tel que \(|f'(x)|\leq M\) pour tout \(x\in [a,b]\). Alors

\[|f(b)-f(a)|\leq M|b-a|.\]

Preuve. On applique l’égalité des accroissements finis. Il existe \(c\in[a,b]\) tel que \(f'(c)=\frac{f(b)-f(a)}{b-a}\). Ainsi,

\[|f(b)-f(a)|\leq |f'(c)|\cdot|b-a|\leq M|b-a|.\]

2.6 Dérivation et monotonie

Définition 2.8 Soit \(I\) un intervalle et \(f\colon I \to \mathbb{R}\) une fonction. On dit que \(f\) est croissante (respectivement strictement croissante) si pour tout \(a,b\in I\), \(a\leq b\implies f(a)\leq f(b)\) (respectivement \(a< b\implies f(a)<f(b)\)).

On dit que \(f\) est décroissante (respectivement strictement décroissante) si pour tout \(a,b\in I\), \(a\leq b\implies f(a)\geq f(b)\) (respectivement \(a< b\implies f(a)>f(b)\)).

On dit que \(f\) est monotone (respectivement strictement monotone) si elle est croissante ou décroissante (respectivement strictement croissante ou strictement décroissante).

Proposition 2.7 Soit \(I\) un intervalle et \(f\colon I \to \mathbb{R}\) une fonction. Si \(f\) est croissante (respectivement décroissante) et dérivable en \(a\) alors \(f'(a)\geq0\) (respectivement \(f'(a)\leq 0\)).

Preuve. Montrons le cas où \(f\) est croissante. Soit \((x_n)\) une suite de \(I\) avec \(x_n\to a\) et \(x_n\neq a\) alors \(\frac{f(x_n)-f(a)}{x_n-a}\geq 0\) et \(\frac{f(x_n)-f(a)}{x_n-a}\to f'(a)\) donc \(f'(a)\geq0\).

Proposition 2.8 Soit \(a,b\in\mathbb{R}\) avec \(a<b\) et \(f\colon [a,b] \to \mathbb{R}\) une fonction dérivable sur \([a,b]\). Si \(f'(x)\geq 0\) (respectivement \(f'(x)>0\)) pour tout \(x\in [a,b]\) alors \(f\) est croissante (respectivement strictement croissante) sur \([a,b]\). De même, si \(f'(x)\leq 0\) (respectivement \(f'(x)<0\)) pour tout \(x\in [a,b]\) alors \(f\) est décroissante (respectivement strictement décroissante) sur \([a,b]\).

Preuve. Si \(f\) n’était pas croissante, on pourrait trouver \(x<y\) tels que \(f(x)>f(y)\). Par l’égalité des accroissements finis, on aurait \(c\in[x,y]\), tel que \(f'(c)=\frac{f(x)-f(y)}{x-y}<0\) et donc une contradiction.

Les autres cas sont similaires.

Théorème 2.7 Si \(f\colon [a,b]\to[c,d]\) est une bijection dérivable telle que \(f'(x)> 0\) (respectivement \(f'(x)<0)\) pour tout \(x\in[a,b]\). Alors \(f\) est inversible d’inverse dérivable avec \((f^{-1})'(x)=\frac{1}{f'(f^{-1}(x))}\).

Preuve. Comme \(f'>0\), la fonction \(f\) est strictement croissante et continue. Par le Théorème 2.3, on sait que \(f\) est une fonction inversible d’inverse continue strictement croissante. Comme \(f\) est dérivable, pour tout \(x\in [a,b]\),

\[\begin{equation} \frac{f(y)-f(x)}{y-x}\to f'(x) \tag{2.2} \end{equation}\]

quand \(y\to x\). En utilisant cette limite pour \(x'=f(x)\) et \(y'=f(y)\), quand \(y'\to x'\), \(y\to x\) par continuité de \(f^{-1}\) et donc la limite (2.2) devient

\[\frac{y'-x'}{f^{-1}(y')-f^{-1}(x')}\to f'(f^{-1}(x'))\]

et en passant à l’inverse

\[\frac{f^{-1}(y')-f^{-1}(x')}{y'-x'}\to \frac{1}{f'(f^{-1}(x'))}.\] Ce qui donne bien que \(f^{-1}\) est dérivable de dérivée \((f^{-1})'(z)=\frac{1}{f'(f^{-1}(z))}\) pour tout \(z\in[c,d]\).

Définition 2.9 Soit \(f\colon I \to \mathbb{R}\) une fonction dérivable. Le tableau de variations de \(f\) est constitué un tableau constitué de trois rangées.

La première contient les valeurs de \(x\) : les bornes de l’intervalle \(I\) et les points d’annulation de la dérivée (les \(x\) tels que \(f'(x)=0\)).
La seconde rangée contient le signe de la dérivée \(f'\). On indique \(0\) en dessous des points d’annulation et \(+\) ou \(-\) sur les intervalles où \(f'(x)>0\) ou \(f'(x)<0\).
La troisième rangée contient le sens de variation de \(f\) notés par une flèche montante ou descendante selon que \(f\) est strictement croissante ou décroissante. On indique aussi les valeurs (ou limites) aux bornes de l’intervalle ainsi que les valeurs de \(f\) aux points d’annulation de \(f'\).

Exemple 2.4 Voici le tableau de variation de la fonction \(f(x)=x(x^2-1)\) dont la dérivée est \(f'(x)=3x^2-1\) et qui s’annule en \(x=\pm\frac{1}{\sqrt{3}}\).

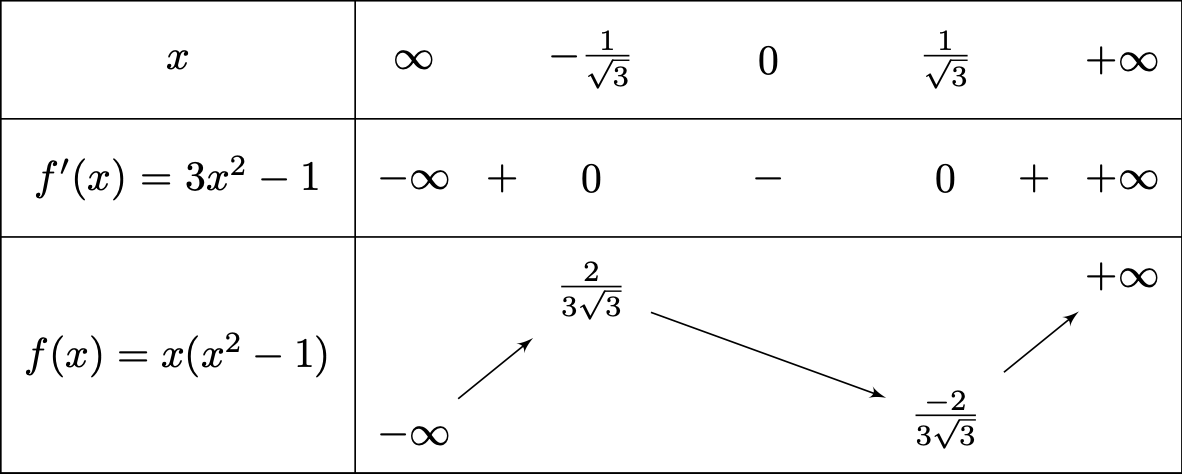
Figure 2.8: Tableau de variations de la fonction \(f(x)=x(x^2-1)\).

2.7 Exponentielle et logarithme

Définition 2.10 La fonction exponentielle est la fonction \(f\colon\mathbb{R}\to\mathbb{R}\) dérivable telle que \(f(0)=1\) et pour tout \(x\in\mathbb{R}\),

\[f'(x)=f(x).\]

On notera cette fonction \(\exp\).

Remarque. L’existence et l’unicité d’une telle fonction, que nous admettrons, demande un argument de résolution d’équation différentielle linéaire du premier ordre.

Figure 2.9: Graphe de la fonction exponentielle.

Lemme 2.2 Soit \(\lambda\in\mathbb{R}\). L’unique fonction \(f\colon\mathbb{R}\to\mathbb{R}\) dérivable telle que \(f(0)=\lambda\) et pour tout \(x\in\mathbb{R}\) \(f'(x)=f(x)\), est la fonction \(x\mapsto \lambda\exp(x)\).

Preuve. Soit \(f\) une telle fonction. Si \(\lambda=0\) alors \(f\) est constante égale à 0. Si \(\lambda\neq 0\) alors \(g=f/\lambda\) vérifie la relation \(g'=g\) et \(g(0)=1\) donc \(g=\exp\).

Proposition 2.9 Pour tout \(a,b\in\mathbb{R}\), \(\exp(a+b)=\exp(a)\exp(b)\) et donc pour tout \(a\in\mathbb{R}\), \(\exp(-a)=\frac{1}{\exp(a)}\).

Preuve. Pour \(a\) fixé, posons \(f(x)=\exp(x+a)\). Alors la fonction \(f\) est la composée de l’exponentielle et de la fonction \(x\mapsto x+a\). Elle est donc dérivable de dérivée, \(f'(x)=\exp(x+a)\cdot 1=f(x)\) et \(f(0)=\exp(a)\). Par le résultat d’unicité sur les équations différentielles, \(f(x)=\exp(a)\exp(x)\). En particulier, pour \(x=b\), on a \(\exp(a+b)=\exp(a)\exp(b)\).

Pour \(b=-a\), cela donne \(1=\exp(0)=\exp(a)\exp(-a)\) et donc \(\exp(-a)=\frac{1}{\exp(a)}\).

Théorème 2.8 La fonction exponentielle réalise une bijection strictement croissante de \(]-\infty,\infty[\) sur \(]0,+\infty[\). Son inverse, appelé logarithme népérien, et noté \(\ln\), est une bijection strictement croissante de \(]0,+\infty[\) sur \(]-\infty,+\infty[\).

Remarque. Ce théorème contient en particulier le fait que \(\lim_{x\to+\infty}\exp(x)=+\infty\) et \(\lim_{x\to-\infty}\exp(x)=0\) et en passant à l’inverse \(\lim_{x\to0}\ln(x)=-\infty\) et \(\lim_{x\to+\infty}\ln(x)=+\infty\).

Preuve. Premièrement, la dérivée de l’exponentielle est toujours positive. Si avait \(\exp(x_0)=0\) alors en posant \(f(x)=\exp(x+x_0)\), on a \(f'(x)=f(x)\) et \(f(0)=\exp(x_0)=0\). Par la propriété sur les équations différentielles énoncée dans la remarque précédente, on aurait \(f(x)=0\) pour tout \(x\in\mathbb{R}\) et donc aussi \(\exp(x)=0\) pour tout \(x\in\mathbb{R}\). Comme \(\exp(0)=1\), on obtient une contradiction.

Ainsi, la fonction exponentielle ne s’annule pas et comme \(\exp(0)>1\), elle est toujours positive par le théorème des valeurs intermédiaires. La fonction exponentielle est donc strictement croissante et dérivable de dérivée strictement positive (\(\exp'(x)=\exp(x)>0\) pour tout \(x\in\mathbb{R}\)). Par le Théorème 2.7, elle est inversible sur tout intervalle \([a,b]\) et strictement croissante. Elle est donc inversible sur \(]-\infty,+\infty[\).

On a \(\exp(x)\geq\exp(0)=1\) pour tout \(x\geq0\) et donc aussi \(\exp'(x)\geq1\) pour tout \(x\geq0\). Par le théorème des accroissements finis, pour tout \(x\geq0\), il existe \(c\in[0,x]\) tel que \[\exp(x)-\exp(0)=\exp'(c)(x-0)\] et donc \(\exp(x)\geq 1+x\) pour tout \(x\geq 0\). Ce qui montre que \(\exp(x)\to+\infty\) quand \(x\to+\infty\) et aussi \(\exp(x)\to 0\) quand \(x\to\infty\) puisque \(\exp(x-x)=1\) et donc \(\exp(x)=\frac{1}{\exp(-x)}\) et \(\exp(-x)\to+\infty\) quand \(x\to -\infty\).

On peut alors appliquer le théorème de la bijection continue pour obtenir l’existence du logarithme népérien \(\ln\) et ses propriétés.

Figure 2.10: Graphe de la fonction logarithme népérien.

Proposition 2.10 Pour tout \(x,y>0\), \(\ln(xy)=\ln(x)+\ln(y)\) et donc pour tout \(x>0\), \(\ln(1/x)=-\ln(x)\). En particulier \(\ln(1)=0\).

Preuve. Posons \(a=\ln(x)\) et \(b=\ln(y)\). On \(\exp(a+b)=\exp(\ln(x))\exp(\ln(y))=xy\). Ce qui donne en passant au logarithme, \(\ln(x)+\ln(y)=a+b=\ln(xy)\). Avec \(y=x\), on obtient \(2\ln(x)=\ln(x)\) et donc \(\ln(1)=0\). Finalement, pour \(y=1/x\), on a \(\ln(1/x)=-\ln(x)\).

Définition 2.11 Pour \(a>0\), on définit l’ exponentielle de base \(a\) comme étant la fonction de \(\mathbb{R}\) dans \(\mathbb{R}\), \(x\mapsto \exp(x\ln(a))\) que l’on notera \(x\mapsto a^x\).

On appelle logarithme en base \(a\) la fonction inverse de l’exponentielle en base \(a\). On note \(\log_a\) cette fonction.

On note \(e=\exp(1)\), ce qui donne \(\ln(e)=1\). Ainsi, \(e^x=\exp(x\ln(e))=\exp(x)\).

Figure 2.11: Exponentielle et logarithme en base 2. Les deux courbes sont symétriques par rapport à la droite d’équation \(y=x\).

Remarque. Cette notation est compatible avec la notation \(a^n=\underbrace{a\times\dots\times a}_{n \textrm{ fois}}\) pour \(n\in\mathbb{N}\). En effet, avec la Proposition 2.9, on a \[\begin{align*} a^n&=\exp(n\ln(a))=\exp\left(\underbrace{\ln(a)+\dots+\ln(a)}_{n\textrm{ fois}}\right)\\ &=\exp(\ln(a))\times\dots\times\exp(\ln(a)) \end{align*}\]

Exemple 2.5 Pour un entier \(n\in\mathbb{N}\), \(\lfloor\log_{10}(n)\rfloor+1\) représente le nombre de chiffres dans l’écriture en base 10 de \(n\) où \(\lfloor x\rfloor\) est la partie entière de \(x\), c’est-à-dire l’entier \(k\in\mathbb{Z}\) tel que \(k\leq x< k+1\).

En effet, un nombre entier \(n\in\mathbb{N}\) s’écrit \(n=\sum_{i=0}^la_i10^i\) où les \(a_i\) sont les chiffres de \(n\) dans l’écriture en base 10 et ce nombre \(N\) de chiffres est \(l+1\). Comme

\[10^l\leq n<10^{l+1}\]

on a \(10^{N-1}\leq n<10^N\), c’est-à-dire \(N-1\leq \log_{10}(n)<N\) et donc \(N\leq \log_{10}(n)+1<N+1\), ce qui donne bien \(N=\lfloor \log_{10}(n)+1\rfloor=\lfloor \log_{10}(n)\rfloor+1\).

De même, pour un entier \(n\), \(\lfloor\log_2(n)\rfloor+1\) représente le nombre de chiffres dans l’écriture en binaire de \(n\).

2.8 Exercices

Exercice 2.1 La fonction de \(\mathbb{R}\) dans \(\mathbb{R}\) donnée par \(x\mapsto \frac{x^4+3x^2+1}{x^2+5}\) est-elle continue ?

Exercice 2.2 La fonction \(f\colon x\mapsto \lfloor x\rfloor\) est-elle continue sur \(\mathbb{R}\) ? On rappelle que \(\lfloor x\rfloor\) est la partie entière de \(x\), c’est-à-dire l’unique entier \(n\) tel que \(n\leq x<n+1\). On pourra dessiner le graphe de cette fonction.

Exercice 2.3 Pour une fonction polynomiale \(f\), on appelle degré de \(f\), la plus grande puissance de \(x\) qui apparait dans l’expression \(f(x)\).

Montrer que toute fonction \(f\) polynomiale de degré impair possède au moins une solution à l’équation \(f(x)=0\).
Donner un exemple de fonction polynomiale \(f\) sur \(\mathbb{R}\) telle que l’équation \(f(x)=0\) n’admette pas de solution.

Exercice 2.4 Soit \(f\colon [a,b]\to [a,b]\) continue avec \(a<b\). Montrer que \(f\) possède un point fixe, c’est-à-dire qu’il existe \(x\in[a,b]\) tel que \(f(x)=x\).

Exercice 2.5 Soit \(f\colon [0,1]\to \mathbb{R}\) continue telle que \(f(0)=f(1)\). Montrer qu’il existe \(x\in[0,1/2]\) tel que \(f(x+1/2)=f(x)\).

Un cycliste parcourt 20 km en une heure. Montrer qu’il existe au moins un intervalle de temps de durée une demi-heure pendant lequel il a parcouru 10 km.

Exercice 2.6 Calculer les dérivées des fonctions données par les expressions suivantes (on précisera le domaine de définition si nécessaire) :

\(f_1(x)=x^a\) avec \(a\in\mathbb{R}\).
\(f_2(x)=a^x\) avec \(a>0\).
\(f_3(x)=\exp(x^3)\).
\(f_4(x)=\frac{x^4\exp(x)}{x^2+2x+3}\).
\(f_5(x)=\left(1+\ln(x)\right)^{1/2}\).

Exercice 2.7 Soit \(f\) une fonction dérivable sur un intervalle \(I\) telle que pour tout \(x\in I\), \(f'(x)=0\). Montrer que \(f\) est constante.

Exercice 2.8 Pour \(a>0\), que vaut \(a^0\) ?

Exercice 2.9 Soit \(n\in\mathbb{N}\) non nul. Justifier que pour tout \(x>0\) il existe un unique nombre \(y\) tel que \(y^n=x\). On notera ce nombre \(\sqrt[n]{x}\).

En utilisant les définitions du cours, justifier que \(\sqrt[n]{x}=x^{\frac{1}{n}}\).

Exercice 2.10 Montrer que pour tout \(a>0\) et \(x>0\), \(\log_a(x)=\frac{\ln(x)}{\ln(a)}\).

Quelle est la relation entre \(\log_a(b)\) et \(\log_b(a)\) ?

Exercice 2.11 Résoudre l’équation \(\ln(x+5)-\ln(x+1)=\ln(2)\).

Exercice 2.12

Donner la partie entière de \(\log_2(10)\).
Que vaut \(\log_2(1024)\) ?
Si \(a\) s’écrit \(a_na_{n-1}\dots a_0\) en base 10, quel encadrement de \(\log_{10}(a)\) pouvez-vous donner ?
Quel nombre \(x>0\) satisfait \(\log_2(x)=-1/2\) ?