Chapitre 3 Suites récurrentes

3.1 Définitions et premières propriétés

Définition 3.1 Soit $I$ un intervalle et $f\colon I\to\mathbb{R}$. Un intervalle $J\subseteq I$ est stable si $f(J)\subseteq J$, c’est-à-dire pour tout $x\in J$, $f(x)\in J$.

Exemple 3.1 Si $I=[a,b]$ et $f\colon [a,b]\to \mathbb{R}$ est monotone avec $f(a),f(b)\in[a,b]$ alors $[a,b]$ est un intervalle stable.

Définition 3.2 Une suite $(x_n)$ est récurrente s’il existe un intervalle $I$, une fonction $f\colon I\to \mathbb{R}$ avec $I$ stable et tels que $x_0\in I$ et $x_{n+1}=f(x_n)$.

Dans la définition ci-dessus, on dit que la suite récurrente $(x_n)$ est associée à la fonction $f$.

Définition 3.3 Soit $I$ un intervalle et $f\colon I\to\mathbb{R}$ une fonction. On dit que $x\in I$ est un point fixe si \[f(x)=x.\]

Proposition 3.1 Soit $(x_n)$ une suite récurrente associée à une fonction $f\colon I\to\mathbb{R}$ continue. Si $\ell\in I$ est une limite finie de $(x_n)$ alors $\ell$ est un point fixe de $f$, c’est-à-dire $f(\ell)=\ell$.

Preuve. Supposons que $x_n$ converge vers $\ell\in I$. Comme $f$ est continue en $\ell$, $f(x_n)$ converge vers $f(\ell)$. Comme la suite $(x_{n+1})$ converge vers $\ell$ et $f(x_n)=x_{n+1}$, on a $f(\ell)=\ell$ par unicité de la limite.

3.2 Comportements des suites récurrentes

Remarque. La première remarque à faire est qu’une suite récurrente est uniquement déterminée par la valeur de $x_0$. Une fois celle-ci fixée, tout le reste de la suite est fixé.

Définition 3.4 Soit $f\colon I\to \mathbb{R}$ une fonction dérivable et $x\in I$ un point fixe. On dit que $x$ est un point fixe attractif si $|f'(x)|<1$.

Proposition 3.2 Soit $f\colon I\to \mathbb{R}$ une fonction de classe $C^1$ sur $I$ est un intervalle ouvert stable. Si $x\in I$ est un point fixe attractif de $f$. Alors il existe un intervalle ouvert $J\subset I$ contenant $x$ tel que pour tout $x_0\in J$, la suite récurrente associée à $f$ de premier terme $x_0$ converge vers $x$.

Preuve. Comme le point $x$ est un point fixe attractif, $|f'(x)|<1$. Posons $\varepsilon=1-|f'(x)|>0$. Par continuité de la fonction $f'$, il existe un intervalle ouvert $J$ contenant $x$ tel que pour tout $y\in J$, $|f'(y)-f'(x)|<\varepsilon/2$ et donc par inégalité triangulaire $|f'(y)|<1-\varepsilon/2$. Posons $\alpha=1-\varepsilon/2<1$. Ainsi, pour pour tout $x_0\in J$, par le théorème des accroissements finis

\[\begin{align*} |f(x_0)-x|&=|f(x_0)-f(x)|\\ &<\alpha|x_0-x|. \end{align*}\]

Ainsi, si $(x_n)$ est la suite récurrente associée à $f$ à partir de $x_0$, on a $|x_1-x|<\alpha|x_0-x|$ et par récurrence sur $n$, $|x_n-x|<\alpha^n|x_0-x|\to0$ quand $n\to\infty$.

Proposition 3.3 Soit $f\colon I\to\mathbb{R}$ une fonction croissante définie sur un intervalle stable. La suite récurrente $(x_n)$ associée à $f$ de premier terme $x_0$ est monotone. Elle est croissante si $x_1\geq x_0$ et décroissante sinon. Elle est convergente si et seulement si elle est bornée.

Preuve. Supposons $x_1\geq x_0$ (l’autre cas se traite de manière analogue) et montrons par récurrence que $(x_n)$ est croissante. L’initialisation ($x_1\geq x_0$) est acquise. Supposons que $x_n\leq x_{n+1}$ pour un certain $n$. Comme $f$ est croissante, on a $f(x_n)\leq f(x_{n+1})$, c’est-à-dire, $x_{n+1}\leq x_{n+2}$ et donc par principe de récurrence on a montré que la suite $(x_n)$ est croissante.

Le dernier point découle du fait que toute suite monotone est convergente si et seulement si elle est bornée. Dans le cas contraire, elle converge vers $+\infty$ dans le cas croissant et $-\infty$ dans le cas décroissant.

Exemple 3.2 On considère la fonction donnée par $f(x)=\frac{x^2}{10}+1$ définie sur $\mathbb{R}$. Cette fonction a deux points fixes qui sont les solutions de l’équation $\frac{x^2}{10}+1=x$ qui sont $5+\sqrt{15}$ et $5-\sqrt{15}$.

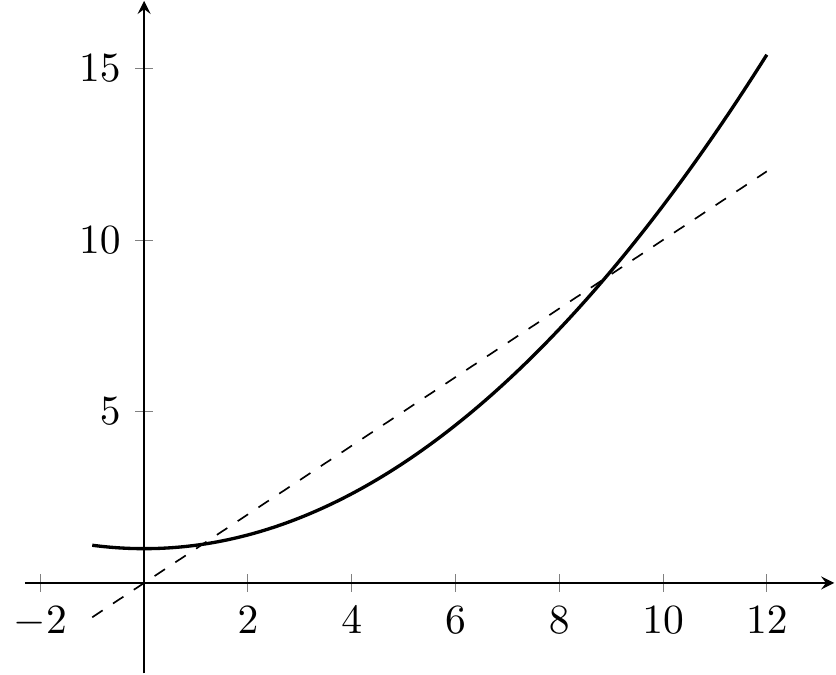
$Les deux points fixes de la fonction $f(x)= x^{2}/10+1$ sont l'intersection de la courbe et de la diagonale $y=x$.$

Figure 3.1: Les deux points fixes de la fonction $f(x)= x^{2}/10+1$ sont l’intersection de la courbe et de la diagonale $y=x$.

Selon la valeur de $x_0$, le comportement de la suite récurrente de relation $x_{n+1}=f(x_n)$ est différent.

Pour $x_0=1$, on a une convergence en escalier croissant.

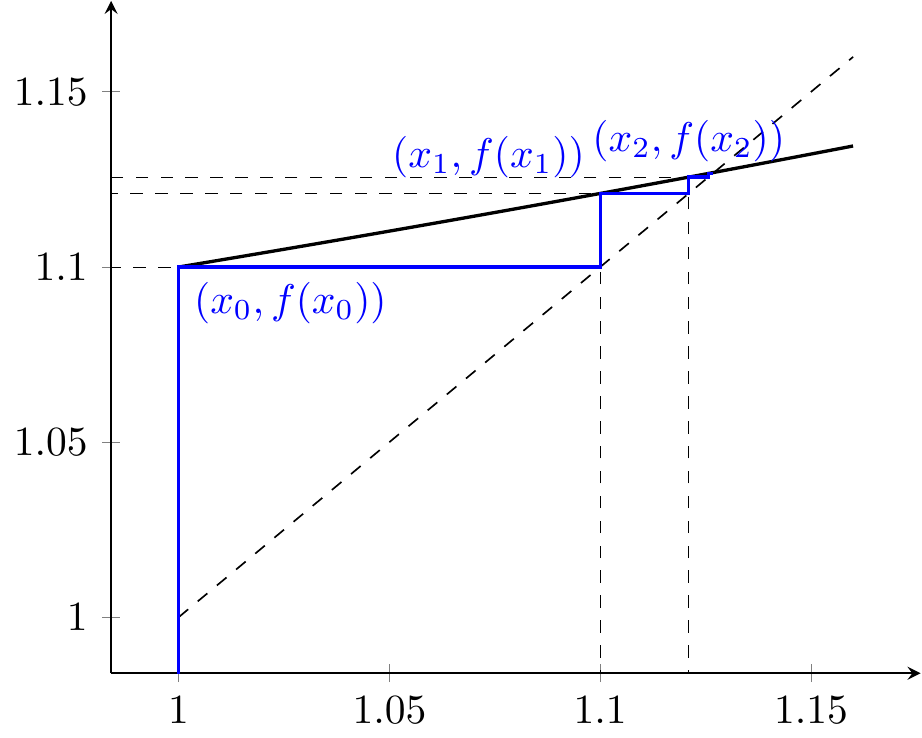
$Convergence en escalier depuis le point $x_0=1$ pour$f(x)= x^{2}/10+1$.$

Figure 3.2: Convergence en escalier depuis le point $x_0=1$ pour$f(x)= x^{2}/10+1$.

Pour $x_0=7$, on a une convergence en escalier décroissant.

$Convergence en escalier depuis le point $x_0=7$ pour $f(x)= x^{2}/10+1$.$

Figure 3.3: Convergence en escalier depuis le point $x_0=7$ pour $f(x)= x^{2}/10+1$.

Pour $x_0=9$, la suite $(x_n)$ est croissante sans être bornée. Elle converge vers $+\infty$.

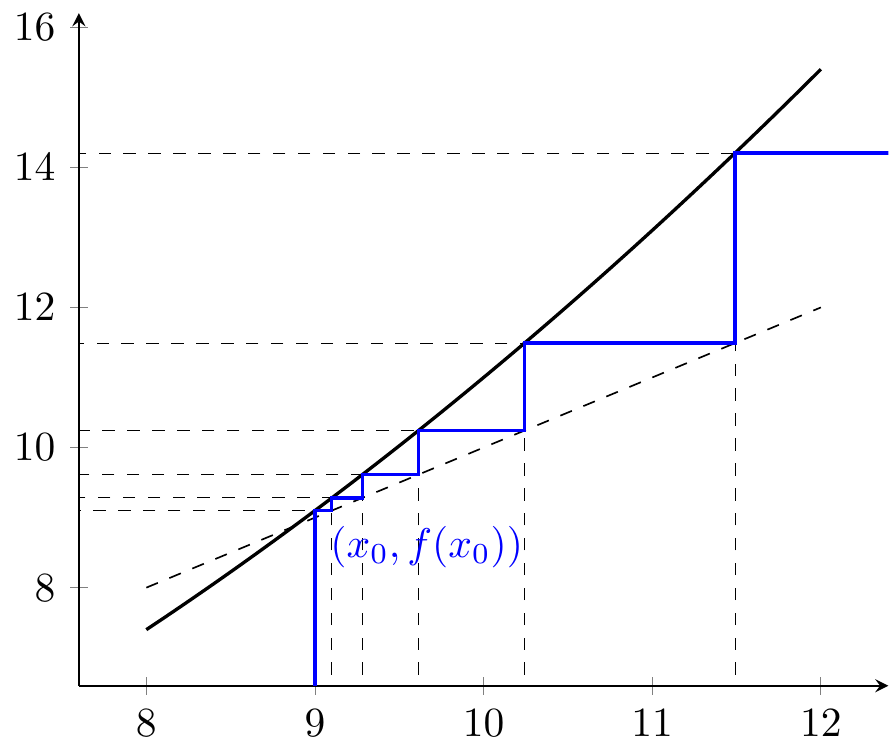
$Convergence en escalier depuis le point $x_0=9$ pour $f(x)= x^{2}/10+1$.$

Figure 3.4: Convergence en escalier depuis le point $x_0=9$ pour $f(x)= x^{2}/10+1$.

Exemple 3.3 On considère la fonction d’expression $f(x)=2-\sqrt{x}$ pour $x>0$. La fonction est décroissante et comme $f(0)=2$ et $f(2)=2-\sqrt(2)\in[0,2]$, l’intervalle $[0,2]$ est stable. La suite récurrente $(x_n)$ associée à $f$ à partir de $x_0=2$ est donc définie pour tout $n\in\mathbb{N}$ et converge vers l’unique point fixe qui est la solution de $2-\sqrt{x}=x$, c’est-à-dire 1. Ce point est attractif, car $|f'(1)|=1/2$.

La convergence est en escargot.

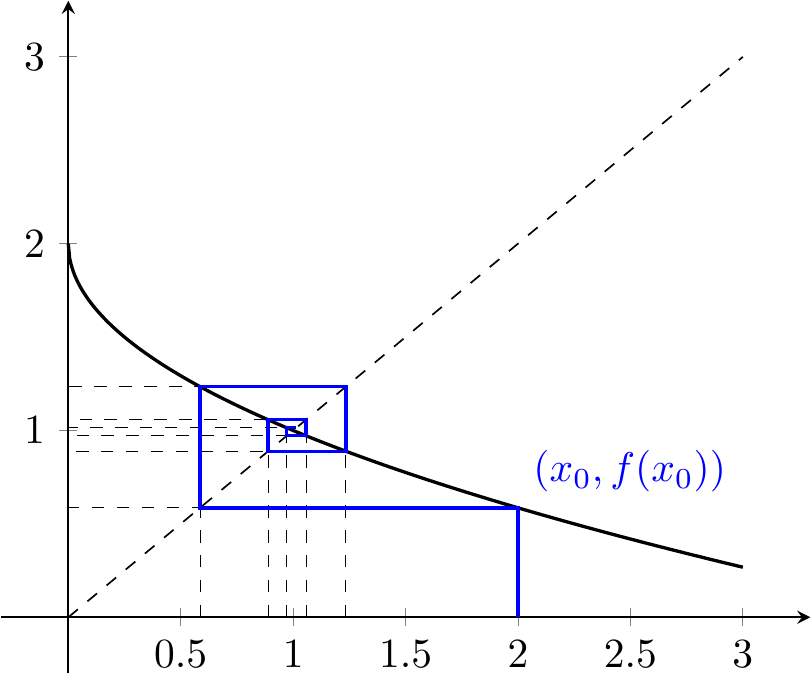
$Convergence en escargot depuis le point $x_0=7$ pour $f(x)=2-\sqrt{x}$.$

Figure 3.5: Convergence en escargot depuis le point $x_0=7$ pour $f(x)=2-\sqrt{x}$.

3.3 Exercices

Exercice 3.1 On considère la suite récurrente définie par $u_{n+1}=\sqrt{1+u_n}$ et $u_0=1$. Étudier le comportement de la suite. Converge-t-elle, a-t-elle une limite infinie ?

Proposer une méthode pour calculer approximativement le nombre d’or $\frac{1+\sqrt{5}}{2}$. On pourra d’abord vérifier que ce nombre d’or est solution de l’équation $x=\sqrt{1+x}$.

Exercice 3.2 On souhaite résoudre l’équation \[\begin{equation} \tag{3.1} x^3-4x+1=0. \end{equation}\]

Dresser le tableau de variation de la fonction $f$ donnée par l’expression $f(x)=x^3-4x+1$.
Justifier que l’Équation (3.1) possède exactement trois solutions $a_1,a_2,a_3$ avec $-2.5<a_1<-2$, $0<a_2<0.5$, $1.5<a_3<2$.
Dessiner l’allure du graphe de $f$.
On pose $\varphi(x)=\frac{1}{4}(x^3+1)$. Montrer que $f(x)=0\iff\varphi(x)=x$.
Parmi les points $a_1,a_2,a_3$, lesquels sont attractifs pour $\varphi$ ?
Montrer que l’intervalle $[0,0.5]$ est stable pour $\varphi$ et en déduire qu’en construisant la suite récurrente $(x_n)$ à partir de $x_0=0$, on obtient une suite $(x_n)$ qui converge vers $a_2$.
La convergence est-elle en escalier ou en escargot ?