Chapitre 5 Comparaisons asymptotiques
5.1 Notations de Landau pour les suites
Définition 5.1 (Domination pour les suites) Soient \((x_n)\) et \((y_n)\) deux suites. On dit que \((x_n)\) est dominée par \((y_n)\) s’il existe \(C>0\) tel que pour tout \(n\in\mathbb{N}\), \(|x_n|\leq C|y_n|\).
On note \(x_n=O(y_n)\).
Remarque. Quand la suite \((y_n)\) ne s’annule pas, cela est équivalent à dire que la suite quotient \((x_n/y_n)\) est bornée.
La notation \(x_n=O(1)\) signifie que la suite \((x_n)\) est bornée.
Définition 5.2 (Négligeabilité pour les suites) Soient \((x_n)\) et \((y_n)\) deux suites. On dit que \((x_n)\) est négligeable devant \((y_n)\) si pour tout \(\varepsilon>0\), il existe \(N\in\mathbb{N}\) tel que pour tout \(n\geq N\), \(|x_n|\leq \varepsilon |y_n|\).
On note \(x_n=o(y_n)\).
Remarque. Quand la suite \((y_n)\) ne s’annule pas, cela est équivalent à dire que la suite quotient \((x_n/y_n)\) tend vers 0.
La notation \(x_n=o(1)\) signifie que la suite \((x_n)\) tend vers 0.
Proposition 5.1 Soient \((x_n)\) et \((y_n)\) deux suites avec \(y_n\) qui ne s’annulent pas. Si \(x_n=o(y_n)\) alors \(x_n=O(y_n)\).
Preuve. Si \(x_n=o(y_n)\) alors \(x_n/y_n\to 0\) et donc \((x_n/y_n)\) est bornée.
Définition 5.3 (Équivalence pour les suites) Soient \((x_n)\) et \((y_n)\) deux suites qui ne s’annulent pas. On dit que \((x_n)\) est équivalente à \((y_n)\) si \(x_n/y_n\to 1\).
On note \(x_n\sim y_n\).
Remarque. Si \(a\in\mathbb{R}\), la notation \(x_n\sim a\) signifie que la suite \((x_n)\) converge vers \(a\).
Définition 5.4 (Suites asymptotiquement du même ordre) On dit que deux suites \((x_n)\) et \((y_n)\) sont asymptotiquement du même ordre si \[x_n=O(y_n)\ \mathrm{et}\ y_n=O(x_n)\] quand \(n\to+\infty\).
On note alors \(x_n=\Theta(y_n)\) (qui se lit “\(x_n\) est un grand thêta de \(y_n\)”).
5.2 Opérations licites
Proposition 5.2 Soit trois suites \((x_n), (y_n), (z_n)\) telles que \((z_n)\) ne s’annulent pas.
Si \(x_n=o(z_n)\) et \(y_n=o(z_n)\) alors \(x_n+y_n=o(z_n)\) et si \(\lambda\in\mathbb{R}\), \(\lambda x_n=o(z_n)\).
Si \(x_n=O(z_n)\) et \(y_n=O(z_n)\) alors \(x_n+y_n=O(z_n)\) et si \(\lambda\in\mathbb{R}\), \(\lambda x_n=0(z_n)\).
Preuve. On considère \(\frac{x_n+y_n}{z_n}=\frac{x_n}{z_n}+\frac{y_n}{z_n}\). Ainsi, si \(x_n=o(z_n)\) et \(y_n=o(z_n)\) alors \(\frac{x_n+y_n}{z_n}\to 0\) et si \(x_n=O(z_n)\) et \(y_n=O(z_n)\) alors \(\frac{x_n+y_n}{z_n}\) est bornée. Ce qui donne le résultat.
Proposition 5.3 Soit quatre suites \((x_n), (y_n), (a_n)\) et \((b_n)\) qui ne s’annulent pas avec \(x_n=o(a_n)\) et \(y_n=o(b_n)\). Alors \(x_ny_n=o(a_nb_n)\).
Preuve. Le quotient \(\frac{x_ny_n}{a_nb_n}\) s’écrit aussi \(\frac{x_n}{a_n}\frac{y_n}{b_n}\) et comme \(\frac{x_n}{a_n}\to0\) et \(\frac{y_n}{b_n}\to0\), on a bien \(\frac{x_ny_n}{a_nb_n}\to 0\).
5.3 Comparaisons usuelles
Proposition 5.4 Pour tous réels \(a<b\), \[n^{a}=o(n^{b}).\]
Preuve. On a \(n^{a}/n^{b}=n^{a-b}\) et comme \(a-b<0\), on a \(n^{a}/n^{b}\to 0\) quand \(n\to+\infty\).
Proposition 5.5 On a \(n=o(\exp(n))\) quand \(n\to +\infty\).
Preuve. Soit \(\varepsilon>0\). Comme \(\exp(n)\to+\infty\), il existe \(A>0\) tel que pour tout \(n\geq A\), \(\exp(n)\geq 2/\varepsilon\). Par égalité des accroissements finis, pour tout \(x>A\), il existe \(c\in[A,n]\) tel que \(\exp(n)-\exp(A)=\exp'(c)(n-A)\). Comme \(\exp'(c)=\exp(c)\), \(\exp(n)-\exp(A)\geq 2/\varepsilon (n-A)\).
Ainsi pour \(n>A\), \[\frac{n}{\exp(n)}=\frac{n}{n-A}\frac{n-A}{\exp(n)-\exp(A)}\frac{\exp(n)-\exp(A)}{\exp(n)}\]
Comme \(\exp(n)\to+\infty\) et \(\frac{\exp(n)-\exp(A)}{\exp(n)}\to 1\) et \(\frac{n}{n-A}\to 1\) et donc pour \(n\) plus grand qu’un certain \(A'>A\), \(\frac{\exp(n)-\exp(A)}{\exp(n)}\leq 2\) et donc pour \(n>A'\), \(\frac{n}{\exp(n)}\leq \varepsilon\). Ce qui montre bien que \(n/\exp(n)\to 0\).
Proposition 5.6 On a \(\ln(n)=o(n)\) quand \(x\to+\infty\).
Preuve. On pose \(y_n=\ln(n)\), on a \(y_n\to +\infty\) quand \(n\to+\infty\). De plus \(\ln(n)/n=y_n/\exp(y_n)\to 0\) quand \(n\to+\infty\).
Corollaire 5.1 Pour tout \(a>0\) et \(b>1\),
\[n^a=o(b^n)\] quand \(n\to\infty\).
Preuve. On écrit
\[\begin{align*} \frac{n^a}{b^n}&=\exp\left(a\ln(n)-n\ln(b)\right)\\ &=\exp\left(n\ln(b)\left(a/\ln(b)\frac{\ln(n)}{n}-1\right)\right) \end{align*}\]
Comme \(\frac{\ln(n)}{n}\to0\), on a \(\left(1-a/\ln(b)\frac{\ln(n)}{n}\right)>1/2\) pour \(n\) assez grand et donc \(n\ln(b)\left(a/\ln(b)\frac{\ln(n)}{n}-1\right)\to-\infty\) et donc \(\frac{n^a}{b^n}\to 0\) quand \(n\to+\infty\).
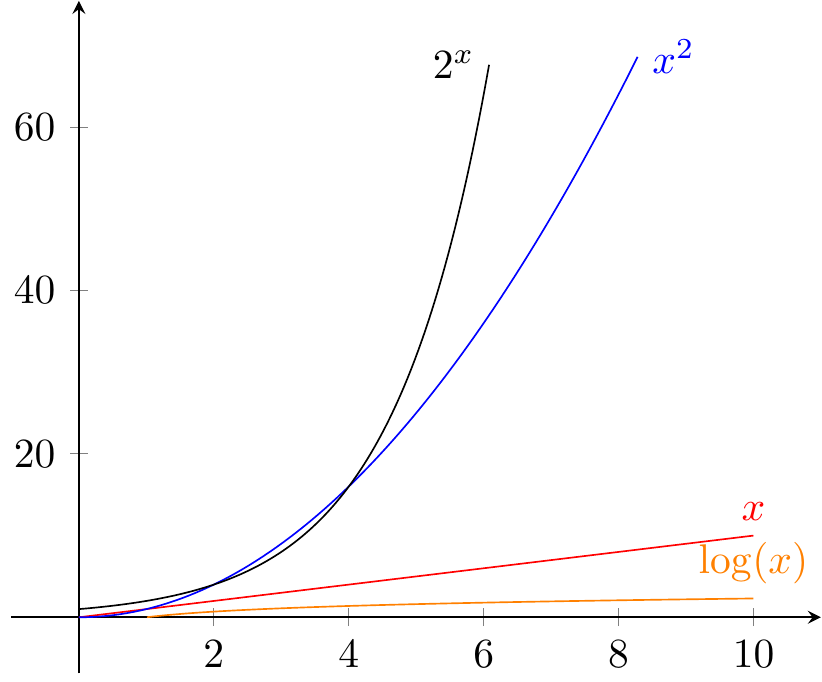
Figure 5.1: Comparaison des croissances des fonctions classiques
5.4 Application à la complexité de quelques algorithmes
Définition 5.5 La compléxité d’un algorithme est la fonction qui donne le nombre maximal d’opérations élémentaires à effectuer pour un algorithme en fonction de la taille des données.
Cette définition de complexité est un peu floue, car il faudrait préciser ce que l’on entend par opération élémentaire et par taille des données. Souvent, ce sera fixé implicitement par le contexte. Par exemple, si on considère un algorithme manipulant des listes, les opérations élémentaires seront l’accès à un élément de cette liste ou la comparaison de deux éléments.
Pour un processeur donné, cette complexité donnera le temps d’exécution de l’algorithme à partir du nombre d’opérations élémentaires réalisables par unité de temps (typiquement en Hertz si l’unité de temps est la seconde). On parle alors de complexité temporelle. Il existe aussi une complexité spatiale qui s’intéresse à la mémoire nécessaire pour l’exécution de l’algorithme.
Remarque. La notion de complexité utilisée ici est celle dans le pire des cas puisque l’on compte le nombre maximal d’opérations à effectuer. Il en existe d’autres comme la complexité en moyenne qui dépend de la distribution statistique du nombre d’opérations à effectuer pour des données de taille \(n\).
Dans la plupart des cas, on ne s’intéresse pas à la complexité exacte, mais à son comportement asymptotique, c’est-à-dire que l’on déterminera une domination par une fonction classique (puissance, exponentielle, logarithme…) de cette complexité.
Exemple 5.1 (Addition) On considère l’addition de deux nombres \(a\) et \(b\) dont l’écriture en base 10 (ce sera la même chose dans n’importe quelle base) est respectivement \(\overline{a_na_{n-1}\dots a_0}\) et \(\overline{b_nb_{n-1}\dots b_0}\) c’est–à-dire comporte au plus \(n\) chiffres.
\[\begin{matrix} &a_na_{n-1}\dots a_0\\ +&b_nb_{n-1}\dots b_0\\ \hline =&c_{n+1}c_nc_{n-1}\dots c_0\\ \end{matrix}\]
L’algorithme appris à l’école nous dit de faire \(n\) fois l’addition élémentaire de deux chiffres \(a_i+b_i\to c_i\) (éventuellement avec une retenue). Ce qui fait \(n\) opérations élémentaires à faire. Ainsi, la complexité de l’addition est en \(O(n)\).
Exemple 5.2 (Multiplication) On considère deux nombres \(a\) et \(b\) deux nombres à \(n\) chiffres (vus comme liste de leurs chiffres). L’algorithme usuel nous dit de faire
ce qui fait \(n^2\) appels aux tables de multiplication puis de faire la somme de ces \(n\) lignes avec des nombres à au plus \(2n\) chiffres. Au total, on obtient une complexité en \(O(n^2)\).
Parmi les opérations classiques en informatique, le tri d’une liste, c’est-à-dire par exemple classement par ordre croissant pour des nombres réels ou classement alphabétique pour des chaînes de caractères, est très courant. Il est important d’avoir des algorithmes efficaces.
Exemple 5.3 (Recherche d'un élément dans une liste non ordonnée) On cherche à savoir si un élément \(a\) appartient à une liste \(L\) non ordonnée avec \(n\) éléments. La méthode la plus simple est de passer en revue les éléments de \(L\) jusqu’à trouver \(a\) (ou pas). Dans le pire des cas, on va faire exactement \(n\) comparaisons. La complexité est donc en \(O(n)\).
Exemple 5.4 (Tri fusion) L’idée est de couper la liste en deux listes de taille identique, d’appliquer récursivement l’algorithme pour trier chacune de ces deux listes puis on fusionne ces deux listes. La complexité de l’algorithme est \(O(n\log(n))\)
# Fonction de fusion de deux listes triées dans l'ordre croissant
def fusion(liste_1, liste_2):
if not liste_1:
return liste_2
if not liste_2:
return liste_1
if liste_1[0] < liste_2[0]:
tete = liste_1.pop(0)
return [tete] + fusion(liste_1, liste_2)
else:
tete = liste_2.pop(0)
return [tete] + fusion(liste_1, liste_2)
#Importation du module math pour les parties entières
import math
#Fonction récursive de tri fusion
def tri_fusion(liste):
longueur = len(liste)
if longueur == 1:
return liste
else:
pivot = math.floor(longueur / 2)
liste_1 = tri_fusion(liste[:pivot])
liste_2 = tri_fusion(liste[pivot:])
return fusion(liste_1, liste_2)Exemple 5.5 (Problème du sac à dos) On considère un sac qui peut supporter un poids maximal \(m\) et une liste de \(n\) objets ayant chacun un poids \(p_i\) et une valeur \(v_i\). Le but est de trouver la liste des objets à emporter pour maximiser la valeur totale emportée \(V\) sans dépasser le poids maximal supporter par le sac à dos.
Si on note \(\delta_i=1\) lorsque le \(i\)-ème objet fait partie de la liste et \(\delta_i=0\) sinon, cela revient à maximiser la somme
\[V=\sum_{i=1}^n\delta_i v_i\] sous la contrainte \(\sum_{i=1}\delta_i p_i\leq m\).
Un algorithme simpliste est d’essayer toutes les possibilités et de retenir celle maximale parmi celles qui conviennent. Pour \(n\) objets, il y a \(2^n\) listes possibles, ce qui donne une complexité en \(O(2^n)\).
Exemple 5.6 (Problème du voyageur de commerce) Un voyageur de commerce doit visiter \(n\) villes et cherche à réaliser le trajet total le plus court. L’algorithme le plus simple pour cela est de calculer pour chaque ordre de visite de ces \(n\) villes, la longueur du trajet et de prendre le court. Comme il y a \(n!\) ordres possible pour \(n\) villes, la complexité est en \(O(n!)\).
Le comportement asymptotique de \(n!\) n’est pas évident mais la formule de Stirling nous apprend que \(n!=O\left(\sqrt{n}\left(\frac{n}{e}\right)^n\right)\) et donc \(n!\) a une croissance bien plus rapide que toute exponentielle !
| Croissance | Nom | Exemple |
|---|---|---|
| \(O(1)\) | Constante | Accès à un élément dans une liste |
| \(O(\log(n))\) avec \(a>1\) | Logarithmique | Recherche dans une liste ordonnée par dichotomie |
| \(O(n)\) | Linéaire | Recherche dans une liste ordonnée |
| \(O(n\log(n))\) | Linéarithmétique | Tri fusion |
| \(O(n^k)\) avec \(k\geq 2\) | Polynomiale | Multiplication |
| \(O(a^n)\) avec \(a>1\) | Exponentielle | Problème du sac à dos |
| \(O(n!)\) | Factorielle | Problème du voyageur de commerce |
5.5 P versus NP
On note \(P\) la classe des problèmes pour lesquels il existe un algorithme dont la complexité est polynomiale (par exemple la multiplication de 2 entiers).
On note \(NP\) la classe des problèmes pour lesquels il existe un algorithme qui vérifie si une valeur particulière est solution avec une complexité polynomiale. Par exemple pour un entier \(n\) que l’on voudrait décomposer en produit \(a\times b\), on peut vérifier si la valeur particulière \((a_0,b_0)\) est une solution en temps polynomial puisqu’il suffit de calculer \(a_0\times b_0\) et de comparer à \(n\).
La classe \(P\) est incluse dans \(NP\). En effet si on considère un problème dans \(P\) pour vérifier qu’une valeur particulière est bien solution, on peut toujours calculer la solution (en temps polynomial donc) et vérifier si la valeur particulière coïncide avec la solution.
On ne sait pas aujourd’hui si \(P=NP\) ou \(P\neq NP\). Par exemple, on ne connait pas d’algorithme qui permet de savoir si un entier \(n\) est premier ou se décompose en produit de deux nombres différents de 1 en temps polynomial. Si on trouvait un tel algorithme la sécurité des algorithmes comme RSA (qui ne réside que sur cette difficulté algorithmique pratique) serait brisée et toutes les méthodes comme HTTPS, SSH et autres tomberaient à l’eau.
Savoir si \(P=NP\) ou non est un des 8 problèmes du millénaire de la fondation Clay qui rapportera un million de dollars aux personnes qui sauront y répondre !
5.6 Exercices
Exercice 5.1 Montrer que si \(x_n\sim y_n\) alors \(x_n=O(y_n)\).
Exercice 5.2 On considère deux suites \((x_n)\) et \((y_n)\) qui ne s’annulent pas. Montrer que
\[x_n\sim y_n \ \iff\ x_n-y_n=o(y_n)\] quand \(n\to +\infty\).
Exercice 5.3 Montrer que la relation \(\sim\) pour les suites qui ne s’annulent pas est bien une relation d’équivalence.
Exercice 5.4 Montrer que la relation “être asymptotiquement du même ordre” est une relation d’équivalence.
Exercice 5.5 On considère trois suites \((x_n),(y_n),(z_n)\) qui ne s’annulent pas avec \(x_n=\Theta(y_n)\) et \(z_n=o(y_n)\) quand \(n\to +\infty\). Montrer que \(x_n+z_n=\Theta(y_n)\) quand \(n\to+\infty\).
Exercice 5.6 Montrer que pour tout \(a,b>0\), \(\log_a(n)=\Theta(\log_b(n))\) et \(n\log_a(n)=\Theta(n\log_b(n))\) quand \(n\to\infty\). Cela justifie de ne pas faire apparaître la base du logarithme dans les croissances logarithmique et linéarithmétique.
Exercice 5.7 Écrire en pseudo-code un algorithme de multiplication de deux matrices carrées de même taille. Quelle est la complexité de cet algorithme en fonction de la taille \(n\) des matrices ?
Exercice 5.8 Écrire en pseudo-code (ou dans votre langage préféré) l’algorithme de Dijkstra comme vu en cours de théorie des graphes puis analyser sa complexité.