Chapitre 4 Approximations

Lorsque l’on fait des calculs, des nombres comme \(\sqrt{2}\), \(e\), \(\ln(2)\) ou encore \(\pi\) apparaissent. Le but de ce chapitre est d’obtenir des approximations de ces nombres.

4.1 Dichotomie

La méthode de dichotomie est celle que nous avons utilisée pour démontrer le théorème des valeurs intermédiaires. Elle fournit aussi de très bonnes estimations. On donne ici une méthode pour une fonction strictement monotone.

Soit \(f\) une fonction continue sur un segment \([a,b]\) strictement croissante avec \(f(a)\) et \(f(b)\) de signes opposés. On cherche \(c\in[a,b]\) tel que \(f(c)=0\). Le théorème des valeurs intermédiaires donne l’existence d’un tel \(c\). La stricte monotonicité implique l’unicité de \(c\).

On pose \(x_0= a\) et \(y_0=b\). On définit \((x_n)\) et \((y_n)\) par récurrence. On suppose \(x_n\) et \(y_n\) déjà définis. Si \(f\left(\frac{x_n+y_n}{2}\right)\leq0\), on pose \(x_{n+1}=\frac{x_n+y_n}{2}\) et \(y_{n+1}=y_n\). Sinon, on pose \(x_{n+1}=x_n\) et \(y_{n+1}=\frac{x_n+y_n}{2}\).

Proposition 4.1 On a

\[|x_n-c|\leq \frac{|b-a|}{2^n}.\]

Exemple 4.1 Le nombre \(\sqrt{2}\) est l’unique racine positive du polynôme \(x^2-2\). On applique la méthode de dichotomie pour \(f(x)=x^2-2\). Comme cette fonction est croissante sur \(\mathbb{R}^+\) et \(f(1)=-1<0\) et \(f(2)=1>0\), on sait que \(\sqrt{2}\in[1,2]\) et donc on commence avec \(x_0=1\) et \(y_0=2\).

On calcule \(\frac{x_0+y_0}{2}=1,5\) et \(f(1,5)=2,25\), on prend donc \(x_1=x_0=1\) et \(y_1=\frac{x_0+y_0}{2}\).

On calcule \(\frac{x_1+y_1}{2}=1,25\) et \(f(1,25)=-0,4375<0\). Ainsi, \(x_2=\frac{x_1+y_1}{2}\) et \(y_2=y_1\).

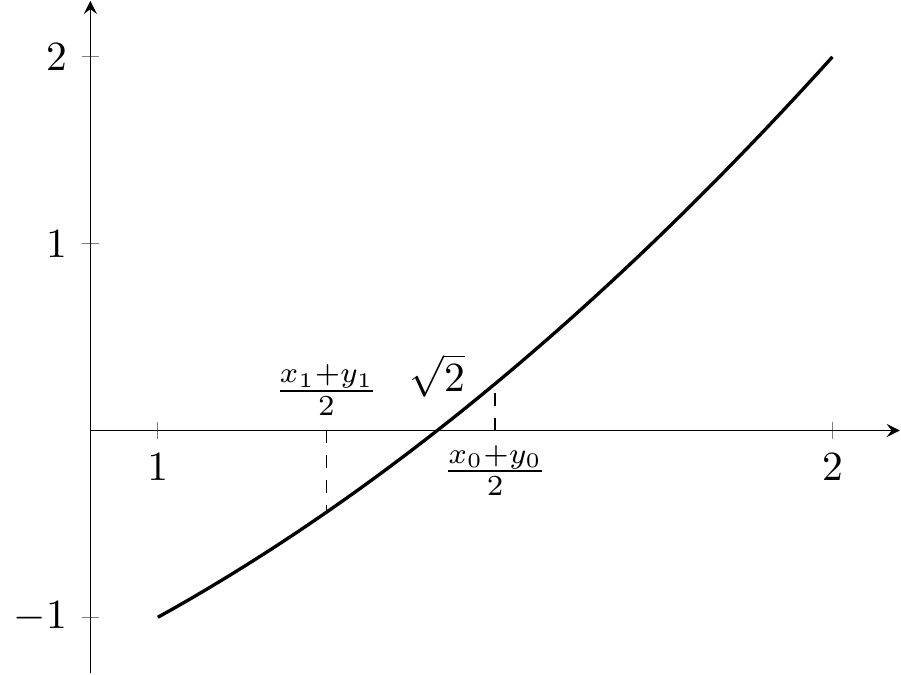
La méthode de dichotomie pour calculer la racine de 2.

Figure 4.1: La méthode de dichotomie pour calculer la racine de 2.

Ainsi, après deux itérations, on a l’approximation \(1,25<\sqrt{2}<1,5\).

4.2 Approximations de \(\pi\) par la méthode d’Archimède

Par définition le nombre \(\pi\) est le rapport entre le périmètre d’un cercle et son diamètre. Le point remarquable est que ce rapport est le même pour tous les cercles.

L’idée originale d’Archimède (mathématicien grec du III-ième siècle avant notre ère) est d’encadrer le périmètre d’un cercle par le périmètre \(p_n\) d’un polygone régulier à \(n\) cotés inscrit au cercle et le périmètre \(P_n\) d’un polygone régulier à \(n\)-côtés circonscrit au cercle.

Si le cercle est de rayon 1, on a alors l’encadrement

\[p_n<2\pi<P_n.\]

Les suites \((p_n)\) et \((P_n)\) sont respectivement croissantes et décroissantes et \(P_n-p_n\to 0\) (il faudrait justifier tout cela, mais on restera au niveau intuitif). Ainsi les suites \((p_n)\) et \((P_n)\) sont adjacentes de limite commune \(2\pi\). On pourra donc approximer \(\pi\) par \(p_n/2\) ou \(P_n/2\) pour \(n\) assez grand (à choisir selon la précision souhaitée).

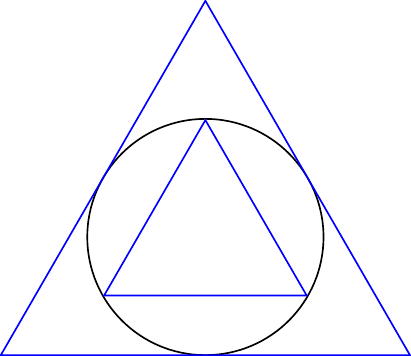
Approximation d'Archimède du périmètre d'un cercle par le périmètre d'un triangle inscrit et un triangle circonscrit.

Figure 4.2: Approximation d’Archimède du périmètre d’un cercle par le périmètre d’un triangle inscrit et un triangle circonscrit.

Par exemple pour \(n=3\), \(p_n/2=\frac{3\sqrt{3}}{2}\) et \(P_n/2=3\sqrt{3}\).

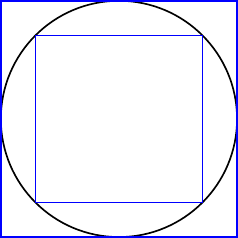
Approximation d'Archimède du périmètre d'un cercle par le périmètre d'un carré inscrit et un carré circonscrit.

Figure 4.3: Approximation d’Archimède du périmètre d’un cercle par le périmètre d’un carré inscrit et un carré circonscrit.

Approximation d'Archimède du périmètre d'un cercle par le périmètre d'un dodécagone inscrit et un dodécagone circonscrit.

Figure 4.4: Approximation d’Archimède du périmètre d’un cercle par le périmètre d’un dodécagone inscrit et un dodécagone circonscrit.

Le polygone régulier inscrit à \(n\) côtés est constitués de \(n\) triangles isocèles avec deux côtés de longueur 1 donc la troisième longueur est \(2\sin\left(\frac{2\pi}{2n}\right)\) et ainsi \(p_n=2n\sin(\pi/n)\).

Le polygone régulier extérieur tangent à \(n\) côtés est constitués de \(n\) triangles isocèles et de hauteur principale 1. Le côté tangent au cercle a donc pour longueur \(2\tan\left(\frac{2\pi}{2n}\right)\) et donc \(P_n=2n\tan\left(\frac{\pi}{n}\right)\).

Ainsi, on a l’encadrement

\[n\sin\left(\frac{\pi}{n}\right)<\pi<n\tan\left(\frac{\pi}{n}\right).\] Posons \(S_n=n\sin\left(\frac{\pi}{n}\right)\) et \(T_n=n\tan\left(\frac{\pi}{n}\right)\).

Des formules géométriques du demi-angle donnent les relations

\[T_{2n}=\frac{2S_nT_n}{S_n+T_n}\ \mathrm{et}\ S_{2n}=\sqrt{S_nT_{2n}}.\]

En partant des carrés inscrits et circonscrits, on a \(T_4=4\) et \(S_4=2\sqrt{2}\geq 2.8\) et cela permet de calculer par récurrence \(S_{2^n}\) et \(T_{2^n}\).

Historiquement, Archimède était parti d’un triangle isocèle et avait divisé l’angle en deux 5 fois et avait donc approché le cercle par des polygones à \(3\times 2^5=96\) côtés et obtenait \[\pi\simeq 22/7\simeq 3,142857.\]

4.3 Méthode de Newton

Le but de la méthode de Newton est de trouver une valeur \(a\) telle que \(f(a)=0\) pour une certaine fonction \(f\). On part d’un point \(x_0\) proche de \(c\) et on définit la suite récurrente \((x_n)\) de la manière suivante

\[x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}.\] Graphiquement, cela correspond à remplacer la fonction \(f\) par la fonction affine donnée par la tangente en \(x_n\). Le point \(x_{n+1}\) est l’intersection de la tangente en \(x_n\) et l’axe des abscisses. La suite \((x_n)\) est bien définie si \(f'(x_n)\) ne s’annule jamais et dans ce le cas théorème suivant (dont la preuve est admise) assure que la suite \(x_n\) converge bien vers le point \(a\) si \(x_0\) est choisi suffisamment proche de \(a\).

Théorème 4.1 Soit \(f\colon I\to\mathbb{R}\) une fonction de classe \(C^1\) et \(a\in I\) tel que \(f(a)=0\) et \(f'(a)\neq0\). Alors il existe \(\alpha>0\) tel que si \(|a-x_0|<\alpha\) alors la suite de la méthode de Newton converge vers \(a\).

Remarque. Si de plus la fonction \(f\) est de classe \(C^2\) et \(x_0\) est suffisamment proche de \(a\) alors la convergence de la méthode de Newton est quadratique. C’est-à-dire qu’il existe \(0<M<1\) tel que

\[|x_n-a|\leq M^{2^n}.\] En particulier, la convergence est très rapide. Par exemple, si \(M=1/10\) alors on gagne 2 décimales de précision à chaque itération.

Exemple 4.2 La méthode de Newton peut être mise en oeuvre pour calculer \(\sqrt{2}\) en utilisant la fonction \(f\) avec \(f(x)=x^2-2\) dont l’unique solution positive à l’équation \(f(x)=0\) est \(\sqrt{2}\).

Comme \(f'(x)=2x\), la relation de récurrence est \(x_{n+1}=x_n-\frac{x_n^2-2}{2x_n}=\frac{x_n}{2}-\frac{1}{x_n}.\)

De plus \(f'(x)\geq 0\) pour \(x\geq 0\) donc la fonction \(f\) est croissante sur \(\mathbb{R}^+\). On calcule, \(f(1)=-1<0\) et \(f(2)=2>0\) donc \(\sqrt{2}\in[1,2]\). On part de \(x_0=2.5\) par exemple.

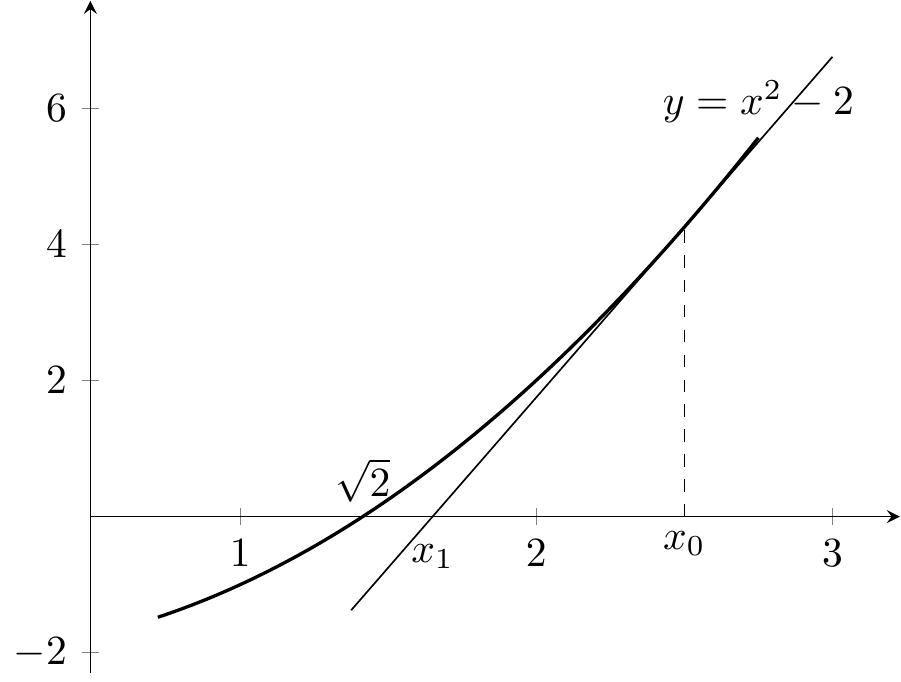
Première itération de la méthode de Newton à partir de $x_0=2.5$

Figure 4.5: Première itération de la méthode de Newton à partir de \(x_0=2.5\)

À la seconde itération, on obtient la figure suivante.
Seconde itération de la méthode de Newton à partir de $x_0=2.5$

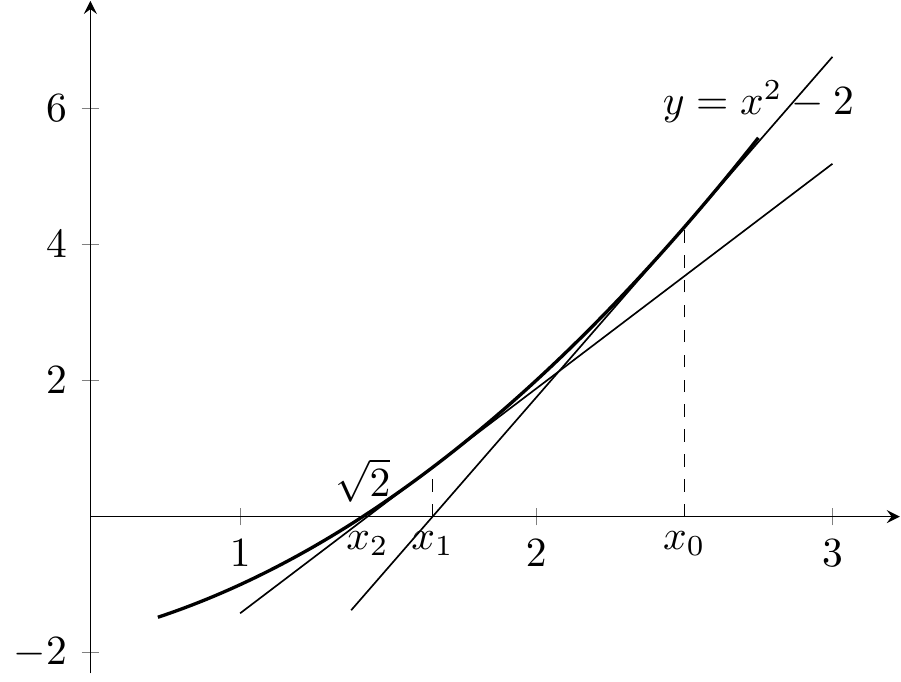
Figure 4.6: Seconde itération de la méthode de Newton à partir de \(x_0=2.5\)

4.4 Méthode d’Euler pour le calcul de la constante d’Euler \(e\)

La méthode d’Euler est une méthode générale de résolution des équations différentielles (les équations dont les inconnues sont des fonctions et qui impliquent des dérivées) comme \(f'=f\). Nous l’appliquons à la fonction exponentielle \(\exp\) et en particulier au nombre d’Euler \(e=\exp(1)\).

Pour \(n>0\), on définit \(x_{i,n}=i/n\) pour \(i=\{0,\dots,n\}\) et \(y_{0,n}=1\) puis \(y_{i+1,n}=y_{i,n}+y_{i,n}1/n\). Ce qui donne \(y_{n,n}=(1+1/n)^n\).

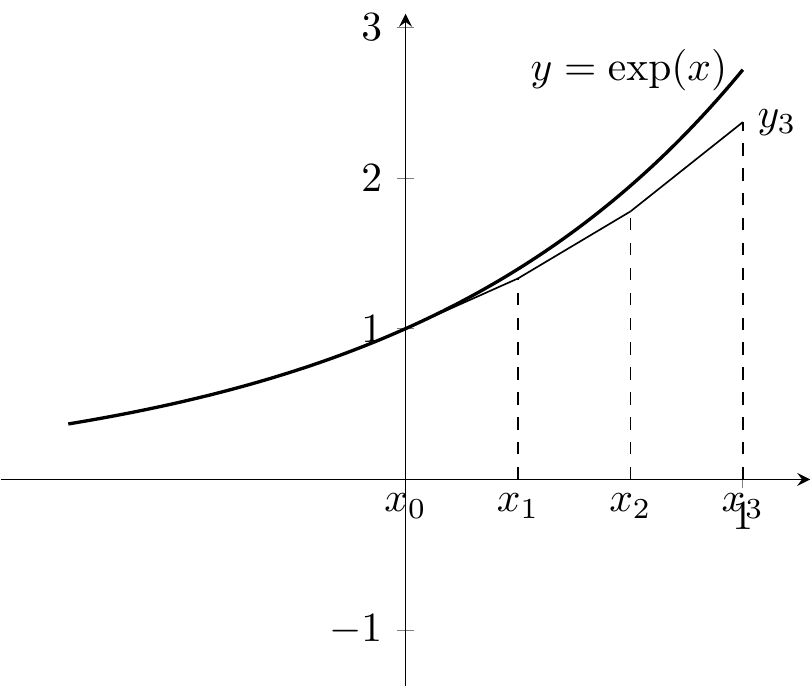
Méthode d'Euler pour calculer le nombre d'Euler $e$

Figure 4.7: Méthode d’Euler pour calculer le nombre d’Euler \(e\)

La convergence de la méthode d’Euler (que nous ne démontrerons pas) donne la limite suivante.

Proposition 4.2 On a \[e=\lim \left(1+1/n\right)^n.\]

4.5 Exercices

Exercice 4.1

  1. Appliquer la méthode de dichotomie pour calculer \(\sqrt{2}\). Vous chercherez la fonction \(f\) et les points \(a,b\) adaptés.
  2. Après \(n\) itérations, quelle est la précision obtenue ?
  3. À l’aide de \(\log_{10}(2)\), indiquer le nombre d’itérations nécessaires pour obtenir l’écriture en base 10 de \(\sqrt{2}\) à \(10^{-k}\) près où \(k\in\mathbb{N}\).

Exercice 4.2 Mettre en oeuvre la méthode de Newton pour calculer \(\sqrt{3}\). Vous donnerez une valeur approchée après 4 itérations et représenterez graphiquement ces 4 étapes en prenant une échelle suffisamment grande sur votre feuille.

Exercice 4.3 On veut calculer l’inverse d’un nombre \(a>0\) à l’aide de la méthode de Newton.

  1. Montrer que \(1/a\) est l’unique zéro de \(f\colon x\mapsto \frac{1}{x}-a\) sur \(\mathbb{R}^+\).
  2. En appliquant la méthode de Newton à \(f\), donner la relation de récurrence entre \(x_{k+1}\) et \(x_k\) et montrer que \(x_{k+1}\) est un polynôme de degré 2 en \(x_k\). En particulier, cette méthode ne fera intervenir que des multiplications pour calculer un inverse.
  3. En utilisant l’encadrement \(1/25<1/23<1/20\) donner une approximation à \(10^{-2}\) près de \(1/23\).
  4. Utiliser la méthode de Newton pour calculer \(1/23\) à \(10^{-5}\). On s’arrêtera lorsque \(|x_{k}-x_{k+1}|<10^{-5}\). On pourra faire les calculs à la main (s’arrêter à \(10^{-4}\) dans ce cas), utiliser une calculatrice, son téléphone portable ou écrire une boucle en Python (ou autre) avec condition d’arrêt. En combien d’itérations êtes-vous arrivés au résultat ?

Exercice 4.4 Un rectangle est dit doré si sa longueur \(a\) et sa largeur \(b\) vérifient la propriété suivante : le rapport de la somme des deux longueurs sur la plus grande est égal à celui de la plus grande sur la plus petite.

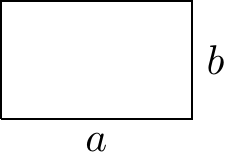
Un rectangle doré.

Figure 4.8: Un rectangle doré.

  1. Traduire la propriété concernant d’un rectangle doré en une équation impliquant \(a\) et \(b\).
  2. Dans ce cas, on note \(\varphi=a/b\) (nombre d’or). Montrer \(\varphi\) est solution de l’équation \(x^2=x+1\).
  3. En établissant le tableau de variations de la fonction \(f(x)=x^2-x-1\), montrer que l’équation \(x^2=x+1\) possède exactement deux solutions, une négative et l’autre positive.
  4. Justifier que \(1<\varphi<2\).
  5. En appliquant la méthode de Newton, calculer \(\varphi\) avec une précision de 3 décimales.
  6. Donner une valeur exacte de \(\varphi\) en résolvant l’équation d’ordre 2.

Exercice 4.5 (Méthode d'Archimède)

  1. Mettre en oeuvre avec Python la méthode d’Archimède pour calculer une valeur approchée avec 15 décimales justes.
  2. Vous mettrez en oeuvre un test d’arrêt et retournerez le nombre d’itérations nécessaires pour atteindre cette précision.
  3. À partir de ce nombre d’itérations, dire quel est le nombre de côtés du polygone régulier par lequel vous approchez le cercle.
  4. Avec l’approximation historique \(\pi\simeq 22/7\), quelle est la précision ?

Exercice 4.6 (Méthode d'Euler)

  1. Montrer que pour \(n\in\mathbb{N}\) \[\left(1+1/n\right)^n=\sum_{k=0}^n\frac{1}{k!}\left(\frac{n!}{(n-k)!n^k}\right).\]
  2. En déduire que \(\left(1+1/n\right)^n\leq\sum_{k=0}^n\frac{1}{k!}\).
  3. Justifier que pour tout \(k\geq 1\), \(\frac{1}{k!}\leq\frac{1}{2^{k-1}}\).
  4. En déduire que pour tout \(m<n\), \[\sum_{k=m+1}^n\frac{1}{k!}\left(\frac{n!}{(n-k)!n^k}\right)\leq \sum_{k=m+1}^n\frac{1}{2^{k-1}}.\]
  5. A l’aide de la formule \[\sum_{i=0}^l\alpha^i=\frac{1-\alpha^{l+1}}{1-\alpha}\] pour \(\alpha\neq1\), montrer \[\sum_{k=m+1}^n\frac{1}{2^{k-1}}=\frac{1}{2^{m+1}}\frac{1-(1/2)^{n-m}}{1-1/2}\leq \frac{1}{2^m}.\]
  6. En écrivant pour \(m< n\), \[\left(1+1/n\right)^n=\sum_{k=0}^m\frac{1}{k!}\left(\frac{n!}{(n-k)!n^k}\right)+\sum_{k=m+1}^n\frac{1}{k!}\left(\frac{n!}{(n-k)!n^k}\right)\] Montrer que \(\left|e-\sum_{k=0}^m\frac{1}{k!}\right|\leq 2^{-m}\) et en déduire que \[\lim_{m\to+\infty}\sum_{k=0}^m\frac{1}{k!}=e.\]
  7. Comparer l’approximation de \(e\) par \(\left(1+1/n\right)^n\) et par \(\sum_{k=0}^n\frac{1}{n!}\). Laquelle est la plus efficace ?