Chapitre 1 Espaces vectoriels

1.1 Corps

La notion de corps généralise les règles de calcul auxquelles nous sommes habitués pour les nombres réels.

Définition 1.1 (corps) Un corps est un ensemble \(\mathbf{K}\) muni de deux lois de composition internes appelées addition “\(+\)” et multiplication “\(\times\)” qui satisfont les propriétés suivantes.

1. L’addition est associative : \(\forall a,b,c\in \mathbf{K}\), \((a+b)+c=a+(b+c)\).
2. L’addition est commutative : \(\forall a,b,c\in \mathbf{K}\), \(a+b=b+a\).
3. La multiplication est associative : \(\forall a,b,c\in \mathbf{K}\), \((a\times b)\times c=a\times(b\times c)\).
4. La multiplication est commutative : \(\forall a,b,c\in \mathbf{K}\), \(a\times b=b\times a\).
5. La multiplication est distributive sur l’addition : \(\forall a,b,c\in \mathbf{K}\)
6. Il existe un élément noté \(0\) tel que pour tout \(a\in \mathbf{K}\), \(a+0=0\) et \(a\times 0=0\).
7. Il existe un élément noté \(1\) tel que pour tout \(a\in \mathbf{K}\), \(a\times 1=a\).
8. Tout élément possède un opposé : \(\forall a\in \mathbf{K},\exists b\in \mathbf{K}\), \(a+b=0\). On note \(-a\) l’opposé de \(a\).
9. Tout élément non nul possède un inverse : \(\forall a\in \mathbf{K}\setminus\{0\},\exists b\in k\), \(a\times b=1\).

Exemple 1.1 Le premier exemple est l’ensemble des nombres réels \(\mathbf{R}\).

Exemple 1.2 L’ensemble des nombres rationnels \(\mathbf{Q}\) forme aussi un corps. Il s’agit des fractions \(p/q\) où \(p\) et \(q\) sont des entiers relatifs avec \(q\neq0\).

Exemple 1.3 Les nombres réels positifs \(\mathbf{R}^+\) ne forment pas un corps : aucun élément non nul ne possède d’opposé.

Exemple 1.4 Les nombres entiers \(\mathbf{Z}\) ne forment pas un corps : les nombres différents de \(-1,0\) et \(1\) ne possèdent pas d’inverse. Par exemple, l’inverse de 2 devrait être 1/2 qui n’est pas dans \(\mathbf{Z}\).

Exemple 1.5 L’ensemble \(\mathbf{C}\) des nombres complexes forme un corps.

Définition 1.2 (corps à deux éléments) Le corps à deux éléments \(\mathbf{F}_2=\mathbf{Z}/2\mathbf{Z}\). il s’agit de l’ensemble \(\{0,1\}\) avec les tables d’addition et de multiplication suivantes :

Table d’addition

• \(0+0=0\)
• \(1+0=1\)
• \(1+1=0\)

Table de multiplication

• \(0\times 1=0\)
• \(1\times 1 =1\)
• \(0\times 0=0\)

Remarque. Le corps \(\mathbf{F}_2=\mathbf{Z}/2\mathbf{Z}\) correspond aux additions et multiplications modulo 2. On l’utilise souvent pour l’arithmétique booléenne où l’on manipule les valeurs VRAI (qui correspond à 1) et FAUX (qui correspond à 0).

Dans la suite, nous utiliserons les deux corps suivants : \(\mathbf{R}\) et \(\mathbf{F}_2\).

1.2 Espaces vectoriels canoniques

Définition 1.3 (Espace vectoriel canonique) Soit \(\mathbf{K}\) un corps et \(n\) un entier positif. L’espace vectoriel canonique de dimension \(n\) sur \(\mathbf{K}\) est \(\mathbf{K}^n\). Un élément de \(\mathbf{K}^n\) est appelé un vecteur. Un élément du corps \(\mathbf{K}\) est appelé un scalaire.

Un vecteur \(v\) est un donc un \(n\)-uplet \((v_1,\dots,v_n)\). Les nombres \(v_i\) sont les coordonnées de \(v\). Le vecteur \((0,\dots,0)\) est appelé vecteur nul.

Définition 1.4 (Addition vectorielle) Soit \(x=(x_1,\dots,x_n)\) et \(y=(y_1,\dots,y_n)\) deux vecteurs. La somme \(x+y\) est le vecteur \((x_1+y_1,\dots,x_n+y_n)\).

Définition 1.5 (Multiplication scalaire) Soit \(\lambda\in \mathbf{K}\) un scalaire et \(v=(v_1,\dots,v_n)\) un vecteur. Le vecteur \(\lambda\cdot v\) est le vecteur \((\lambda v_1,\dots,\lambda v_n)\).

Exemple 1.6 L’espace vectoriel \(\mathbf{F}_2^n\) correspond aux mots binaires de longueur \(n\).

Remarque. Il existe une notion abstraite d’espace vectoriel sur un corps \(\mathbf{K}\) que nous n’aborderons pas ici. Nous n’utiliserons que les espaces vectoriels canoniques ainsi que leurs sous-espaces. Un espace vectoriel abstrait est essentiellement un ensemble \(E\) avec une addition et une multiplication scalaire.

Remarque. On écrit les vecteurs en ligne ou en colonne. Par exemple \((1,0,3)\) ou \(\begin{pmatrix} 1\\ 0\\ 3\end{pmatrix}\). Le choix de l’un ou l’autre n’a souvent pas d’importance, mais ce le sera lorsque nous ferons des multiplications matricielles.

Remarque. On écrit les vecteurs avec des parenthèses ou des crochets. Cela ne change rien. Par exemple, \(\begin{pmatrix} 1\\ 0\\ 3\end{pmatrix}\)et \(\begin{bmatrix} 1\\ 0\\ 3\end{bmatrix}\) représentent le même vecteur.

Proposition 1.1 L’espace vectoriel \(\mathbf{K}^n\) vérifie les propriétés suivantes :

1. Associativité de l’addition vectorielle: \(\forall u,v,w\in\mathbf{K}^n\), \(u+(v+w)=(u+v)+w\).
2. Commutativité de l’addition vectorielle : \(\forall u,v\in \mathbf{K}^n\), \(u+v=v+u\).
3. Associativité de la multiplication scalaire : \(\forall u\in\mathbf{K}^n\), \(\forall \lambda,\mu\in\mathbf{K}\), \(\lambda\cdot(\mu\cdot u)=(\lambda\cdot \mu)u\).
4. Distributivité de la multiplication scalaire sur l’addition vectorielle : \(\forall \lambda\in\mathbf{K},\ u,v\in \mathbf{K}^n\), \(\lambda(u+v)=\lambda u+\lambda v\).

Preuve. Cela découle des propriétés d’associativité, distributivité et commutativité dans \(\mathbf{K}\) lorsque l’on regarde coordonnée par coordonnée.

1.3 Sous-espaces vectoriels

On fixe un corps \(\mathbf{K}\) et un entier positif \(n\).

Définition 1.6 Un sous-espace vectoriel de \(\mathbf{K}^n\) est un sous-ensemble non vide \(E\) de \(\mathbf{K}^n\) qui vérifie les deux propriétés suivantes :

1. (Stabilité par addition) Pour tout \(u,v\in E\), \(u+v\in E\)
2. (Stabilité par multiplication scalaire) Pour tout \(v\in E\) et \(\lambda\in \mathbf{K}\), \(\lambda v\in E\).

Exemple 1.7 Dans \(\mathbf{R}^2\), la droite d’équation \(x-y=0\) est un sous-espace vectoriel.

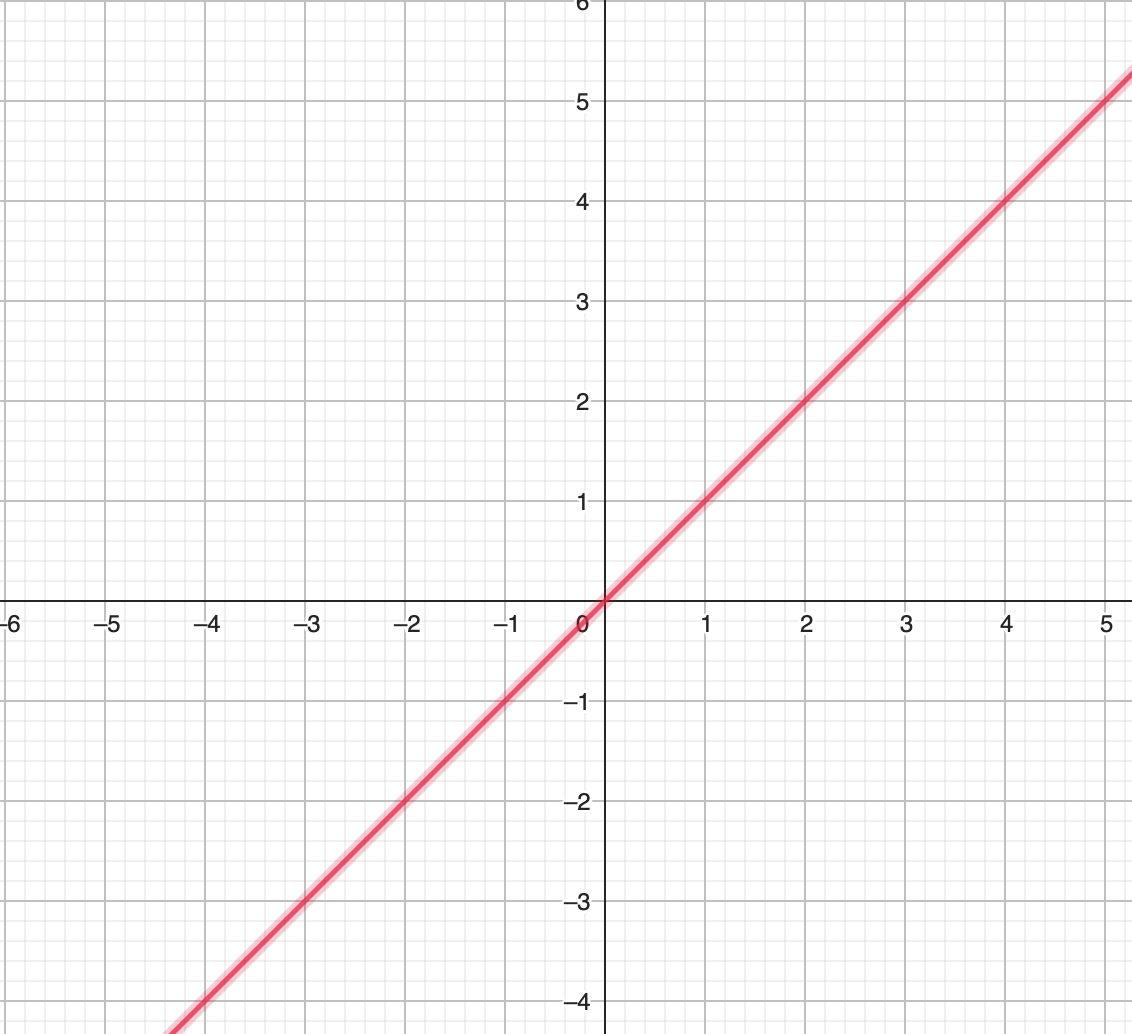
Figure 1.1: Droite x-y=0

Exemple 1.8 Dans \(\mathbf{R}^3\), le plan d’équation \(x+y+z=0\) est un sous-espace vectoriel.

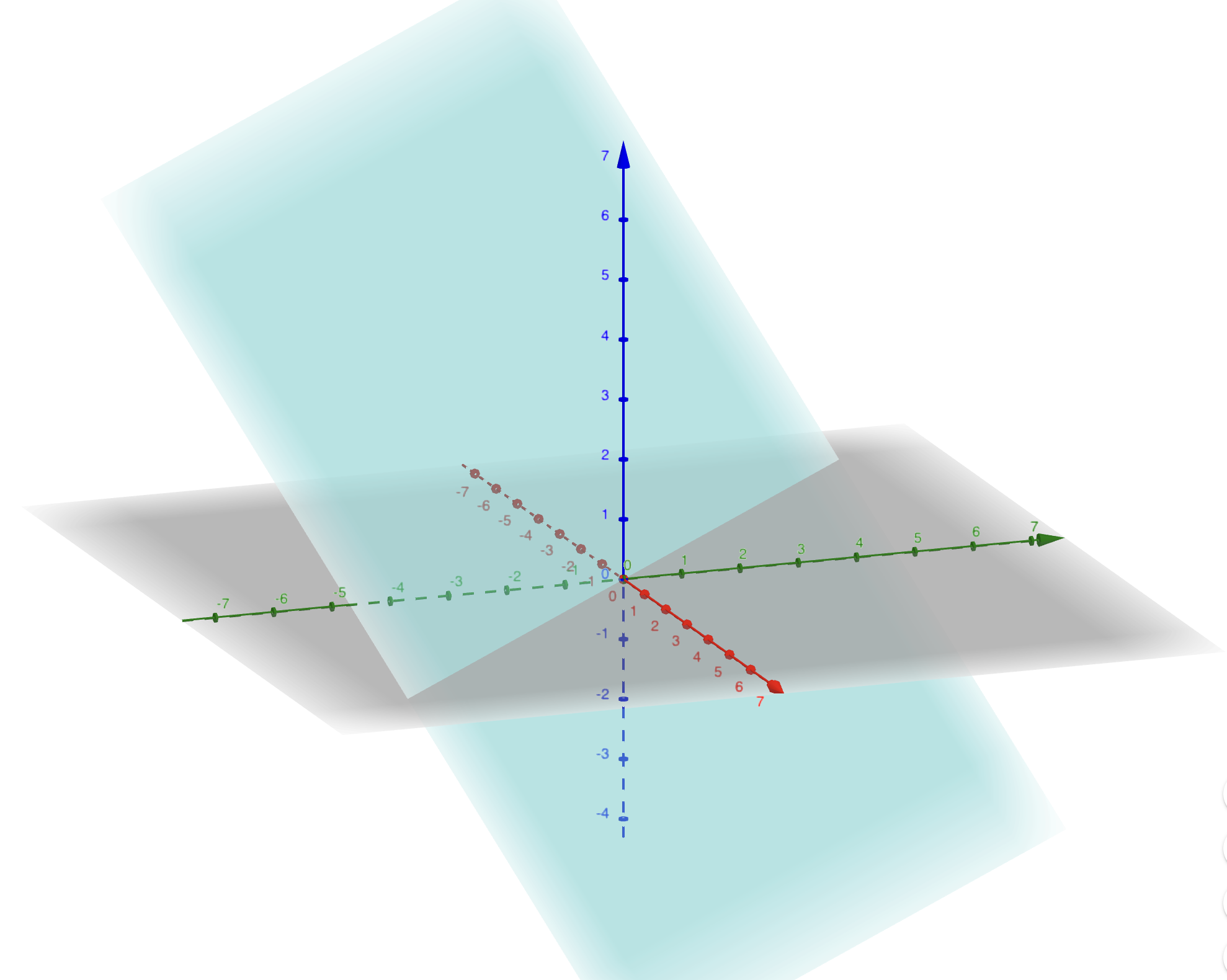
Figure 1.2: Plan x+y+z=0

Remarque. Un sous-espace vectoriel \(E\) contient toujours le vecteur nul 0. En effet, comme \(E\neq\emptyset\), il existe \(v\in E\) et dont \(0=v+(-1)v\in E\).

En pratique, lorsque l’on veut montrer qu’un sous-ensemble est un sous-espace vectoriel, pour vérifier que l’ensemble n’est pas vide, il suffit de montrer qu’il contient le vecteur nul.

Proposition 1.2 L’intersection de deux sous-espaces vectoriels est un sous-espace vectoriel.

Preuve. Soit \(E_1\) et \(E_2\) deux sous-espaces vectoriels. Le vecteur nul appartient à \(E_1\) et \(E_2\) donc \(E_1\cap E_2\neq\emptyset\).

Soit \(u,v\in E_1\cap E_2\). Alors comme \(E_1\) et \(E_2\) sont des sous-espaces vectoriels, \(u+v\in E_1\) et \(u+v\in E_2\) donc \(u+v\in E_1\cap E_2\). De même, pour tout \(u\in E_1\cap E_2\) et \(\lambda\in \mathbf{K}\), \(\lambda v\in E_1\cap E_2\).

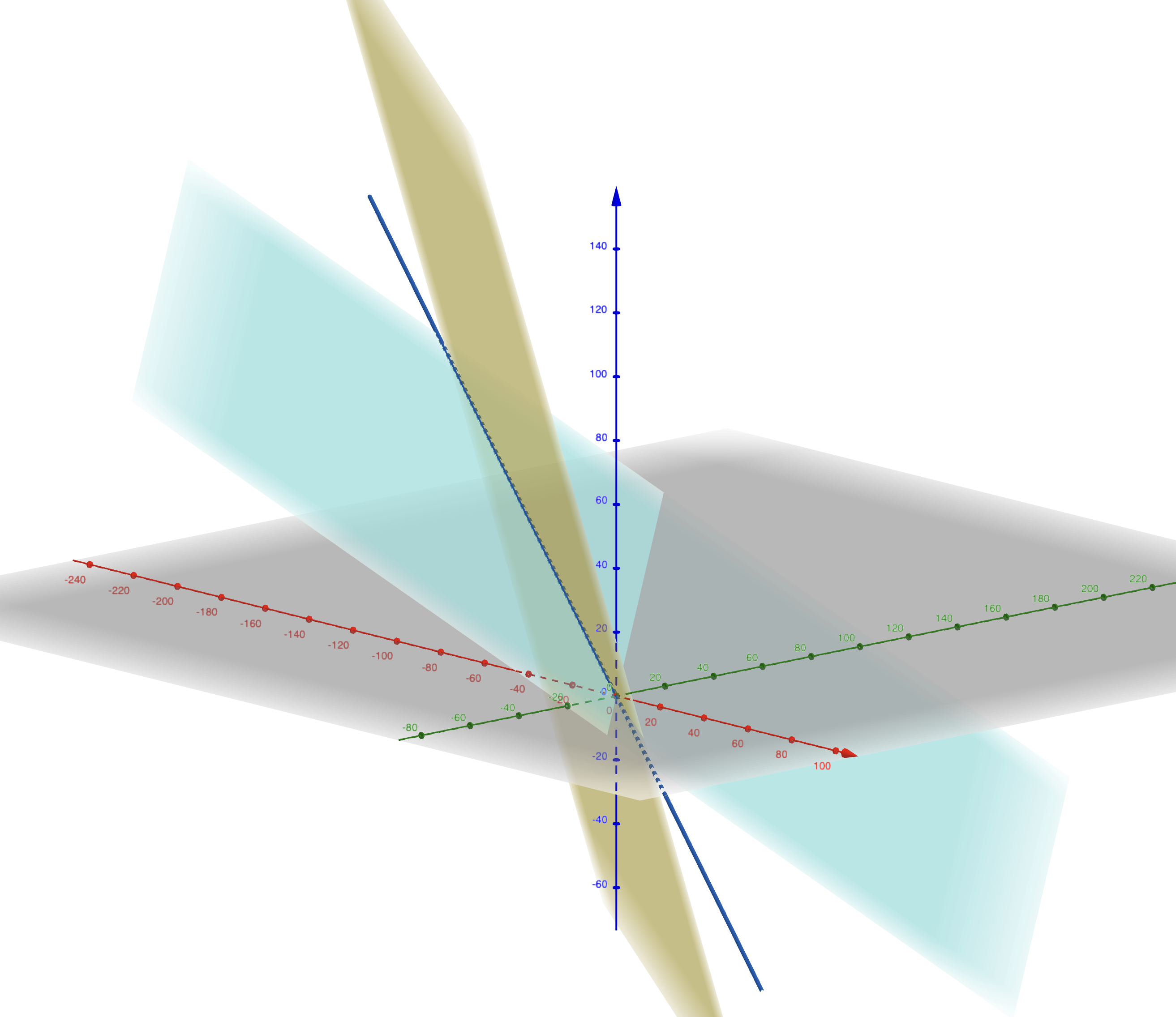
Figure 1.3: Intersection de deux plans qui est une droite

1.4 Bases

Définition 1.7 Soit \(F\) un sous-ensemble de l’espace vectoriel \(\mathbf{K}^n\). Un vecteur \(v\in \mathbf{K}^n\) est une combinaison linéaire d’éléments de \(F\), s’il existe \(v_1,\dots,v_k\in F\) et \(\lambda_1,\dots,\lambda_k\in\mathbf{K}\) tels que

\[v=\lambda_1 v_1+\dots+\lambda_k v_k.\] Les nombres \(\lambda_1,\dots,\lambda_k\) s’appellent les coefficients de la combinaison linéaire.

Exemple 1.9 Le vecteur \(u=\begin{bmatrix}3\\6\end{bmatrix}\) est combinaison linéaire des vecteurs \(e_1=\begin{bmatrix}1\\4\end{bmatrix}\) et \(e_2=\begin{bmatrix}1\\1\end{bmatrix}\) car

\[u=1\times e_1+2\times e_2.\]

Lemme 1.1 Soit \(F\) un sous-ensemble de l’espace vectoriel \(\mathbf{K}^n\). L’ensemble des combinaisons linéaires d’éléments de \(F\) forme un sous-espace vectoriel de \(\mathbf{K}^n\).

Preuve. Notons \(E\) pour l’ensemble des combinaisons linéaires d’éléments de \(F\). Le vecteur nul s’écrit \(0\cdot v\) pour \(v\in F\) donc \(0\in E\) et \(E\neq\emptyset\).

Soit \(v\in E\) et \(\lambda\in\mathbf{K}\). Alors il existe \(v_1,\dots,v_k\in F\) et \(\lambda_1,\dots,\lambda_k\in\mathbf{K}\) tels que \(v=\lambda_1 v_1+\dots+\lambda_k v_k.\) On a

\[\begin{align} \lambda v&=\lambda(\lambda_1 v_1+\dots+\lambda_k v_k)\\ &=(\lambda\lambda_1) v_1+\dots+(\lambda\lambda_k) v_k \end{align}\]

Ainsi, \(\lambda v\) est bien une combinaison linéaire des \(v_i\) et \(\lambda v\in E\).

Soit \(u,v\in E\). Alors il existe \(u_1,\dots,u_k\in F\) et \(\lambda_1,\dots,\lambda_k\in\mathbf{K}\) tels que \(u=\lambda_1 u_1+\dots+\lambda_k u_k\) et \(v_1,\dots,v_l\in F\) et \(\mu_1,\dots,\mu_l\in\mathbf{K}\) tels que \(v=\mu_1 v_1+\dots+\mu_l v_l.\) Ainsi,

\[\begin{align} u+v &= (\lambda_1 u_1+\dots+\lambda_k u_k)+(\mu_1 v_1+\dots+\mu_l v_l)\\ &= \lambda_1 u_1+\dots+\lambda_k u_k+\mu_1 v_1+\dots+\mu_l v_l \end{align}\]

et donc \(u+v\) est une combinaison linéaire des \(u_i\) et \(v_j\) qui sont des éléments de \(F\) et donc \(u+v\in E\).

Définition 1.8 Soit \(F\) un sous-ensemble de l’espace vectoriel \(\mathbf{K}^n\). Le sous-espace vectoriel engendré par \(F\) est l’ensemble des combinaisons linéaires d’éléments de \(F\).

Définition 1.9 Soit \(E\) un sous-espace vectoriel de \(\mathbf{K}^n\) et \(F\) un sous-ensemble de \(E\). On dit que \(F\) est une famille génératrice si \(E\) l’espace vectoriel engendré par \(F\).

Autrement dit, \(F\) est une famille génératrice du sous-espace vectoriel \(E\) si tout élément de \(E\) est une combinaison linéaire d’éléments de \(F\). Dans ce cas, on dit que \(E\) est engendré par \(F\) et on note \(E=\mathrm{Vect}(F)\).

Exemple 1.10 Voici quelques exemples

1. L’ensemble \(E\) tout entier est une famille génératrice de lui-même (tout élément \(v\in E\), s’écrit \(v=1\cdot v\)).
2. L’espace \(\mathbf{R}^2\) est engendré par les vecteurs \(e_1=(1,0)\) et \(e_2=(0,1)\). En effet, tout vecteur de \(\mathbf{R}^2\) s’écrit sous la forme \((x,y)\) qui se décompose en \(xe_1+ye_2\).
3. Dans \(\mathbf{R}^3\), L’ensemble \(E=\{(x,y,z), x+y+z=0\}\) est un sous-espace vectoriel engendré par les vecteurs \(u=(1,-1,0)\) et \(v=(0,-1,1)\). En effet si \((x,y,z)\in E\) alors \(x\cdot u+z\cdot v=(x,-x-z,z)=(x,y,z)\) car \(y=-x-z\) (comme \(x+y+z=0\)).

Remarque. Pour un sous-espace vectoriel donné, il n’y pas du tout unicité d’une famille génératrice. Par exemple, l’espace \(\mathbf{R}^2\) est engendré par la famille \(\{(1,0),(0,1)\}\) mais aussi par la famille \(\{(1,1),(1,-1)\}\) :

\[\begin{align} (x,y)&=\frac{x}{2}\left[(1,1)+(1,-1)\right]+\frac{y}{2}\left[(1,1)-(1,-1)\right]\\ &=\left(\frac{x}{2}+\frac{y}{2}\right)(1,1)+\left(\frac{x}{2}-\frac{y}{2}\right)(1,-1) \end{align}\]

Définition 1.10 Une famille \(F\) de \(\mathbf{K}^n\) est libre si aucun de ses éléments ne peut s’écrire comme combinaison linéaire des autres éléments de \(F\).

Une famille qui n’est pas libre est appelée famille liée.

Définition 1.11 Une combinaison linéaire \(\lambda_1 u_1+\dots+\lambda_k u_k\) est dite triviale si \(\lambda_1=\dots=\lambda_k=0\) et elle dite nulle si \(\lambda_1 u_1+\dots+\lambda_k u_k=0\).

Remarque. Une combinaison linéaire triviale est toujours nulle mais la réciproque n’est pas toujours vraie. Exercice : trouver un contre-exemple !

Lemme 1.2 Une famille \(F\) est libre si et seulement si toute combinaison linéaire nulle d’éléments de \(F\) est triviale:

\[\forall u_1,\dots,u_k\in F,\ \lambda_1,\dots,\lambda_k\in\mathbf{K}; \lambda_1 u_1+\dots+\lambda_k u_k=0\implies \lambda_1=\dots=\lambda_k=0.\]

Preuve. En passant à la contraposée, l’énoncé est équivalent à “\(F\) est liée si et seulement s’il existe une combinaison linéaire d’éléments de \(F\) nulle non triviale”.

Soit \(u_1,\dots,u_k\in F\). Si \(u_i\) est combinaison linéaire des autres \(u_j\) alors, il existe \(\lambda_1,\dots,\lambda_{i-1},\lambda_{i+1},\dots,\lambda_k\in\mathbf{K}\) tels que

\[u_i=\lambda_1u_1+\dots+\lambda_{i-1}u_{i-1}+\lambda_{i+1}u_{i+1}+\dots+\lambda_nu_n\] et donc \[\lambda_1u_1+\dots+\lambda_{i-1}u_{i-1}-u_i+\lambda_{i+1}u_{i+1}+\dots+\lambda_nu_n=0\] ce qui donne une combinaison linéaire nulle non triviale (le coefficient devant \(u_i\) est non nulle).

Réciproquement, soit \(u_1,\dots,u_k\in F\) et \(\lambda_1 u_1+\dots+\lambda_k u_k=0\) une combinaison nulle. Par l’absurde supposons qu’il existe \(\lambda_i\neq0\) alors

\[u_i=\frac{1}{\lambda_i}\left(\sum_{j\neq i}\lambda_j u_j\right)\]

et donc \(u_i\) est combinaison linéaire des autres \(u_j\). Ce qui contredit la liberté. Ainsi, tous les \(\lambda_i\) sont nuls et la combinaison linéaire est triviale.

Exemple 1.11 Quelques exemples.

1. La famille \(\{(1,0),(0,1),(1,1)\}\) est liée car \((1,1)=(1,0)+(0,1)\).
2. La famille \(\{(1,1),(1,-1)\}\) est libre. En effet si \(\lambda(1,1)+\mu(1,-1)=(0,0)\) alors en résolvant le système

\[\left\{\begin{matrix} \lambda+\mu&=0\\ \lambda-\mu&=0 \end{matrix} \right.\]

on trouve \(\lambda=0\) et \(\mu=0\). Ce qui montre que la famille est libre.

Définition 1.12 Soit \(E\) un sous-espace vectoriel de \(\mathbf{K}^n\). Une base de \(E\) est une famille libre et génératrice de \(E\).

Exemple 1.12 La famille \((e_1,\dots,e_n)\) où \(e_i=(0,\dots,0,1,0,\dots,0)\) avev un 1 en \(i\)-ième position est une base de \(\mathbf{K}^n\) appelée base canonique. Les coordonnées \(v_i\) d’un vecteur \(v=(v_1,\dots,v_n)\) sont exactement les coordonnées de \(v\) dans la base canonique puisque

\[v=\sum_{i=1}^nv_ie_i.\]

Lemme 1.3 Soit \(E\) un sous-espace vectoriel de \(\mathbf{K}^n\). Une famille \(\mathcal{B}=(u_1,\dots,u_k)\), où chaque \(u_i\in E\), est une base de \(E\) si et seulement si pour tout vecteur \(u\in E\), il existe un unique \(k\)-uplet \((\lambda_1,\dots,\lambda_k)\in\mathbf{K}^k\) tel que \[u=\lambda_1 u_1+\dots+\lambda_k u_k.\]

Les nombres \(\lambda_1,\dots,\lambda_k\in\mathbf{K}\) s’appellent alors les coordonnées de \(u\) dans la base \(\mathcal{B}\). On prêtera attention au fait qu’une base n’est pas seulement un sous-ensemble mais une suite ordonnée de vecteurs.

Preuve. L’existence de \((\lambda_1,\dots,\lambda_k)\in\mathbf{K}^k\) est équivalent au fait que la famille est génératrice.

S’il y a deux \(k\)-uplets \((\lambda_1,\dots,\lambda_k)\in\mathbf{K}^k\) et \((\mu_1,\dots,\mu_k)\in\mathbf{K}^k\) tels que

\[u=\lambda_1 u_1+\dots+\lambda_k u_k\]

et

\[u=\mu_1 u_1+\dots+\mu_k u_k\] alors \[(\lambda_1-\mu_1)u_1+\dots+(\lambda_k-\mu_k)u_k=0.\]

Ce qui donne une combinaison linéaire nulle. Celle-ci est triviale si seulement si \(\lambda_i=\mu_i\) pour tout \(i\). Ainsi, l’unicité de l’écriture en combinaison linéaire des \(u_i\) est équivalente à la liberté de \((u_1,\dots,u_k)\).

Proposition 1.3 Soit \(E\) un sous-espace vectoriel de \(\mathbf{K}^n\). Si \(\{u_1,\cdots,u_k\}\) est une famille génératrice de \(E\) alors toute famille de \(E\) avec strictement plus de \(k\) éléments est liée.

Preuve. On montre le résultat par récurrence sur \(k\).

Si \(k=0\) alors \(E=\{0\}\). Le seul élément de \(E\) est le vecteur nul et donc toute combinaison linéaire est nulle.

On suppose le résultat pour \(k-1\geq 0\). Soit \(E\) un sous-espace engendré par \(k\) vecteurs \(u_1,\dots,u_{k}\) et soit \(F=\{f_1,\dots,f_{k+1}\}\) une famille de \(k+1\) (ce qui montre le résultat pour toute famille de cardinal plus grand). Comme la famille \(\{u_1,\dots,u_{k}\}\) est génératrice, pour tout \(1\leq j\leq k+1\), il existe \(a_{1,j},\dots,a_{k,j}\) tels que

\[f_j=\sum_{i=1}^ka_{i,j}u_i.\] Si tous les \(a_{k,j}\) pour \(j=1,\dots,k+1\) sont nuls alors la famille est dans \(\mathrm{Vect}(u_1,\dots,u_{k-1})\) et par hypothèse de récurrence, on sait qu’elle est liée. Sinon, quitte à échanger l’ordre des éléments de \(F\), on peut supposer que \(a_{k,k+1}\neq0\). Pour \(1\leq j\leq k\), posons

\[\begin{align} f'_j&=f_j-\frac{a_{k,j}}{a_{k,k+1}}f_{k+1}\\ &=\sum_{i=1}^k\left(a_{i,j}-\frac{a_{k,j}}{a_{k,k+1}}a_{i,k+1}\right)u_i\\ &=\sum_{i=1}^{k-1}\left(a_{i,j}-\frac{a_{k,j}}{a_{k,k+1}}a_{i,k+1}\right)u_i\\ \end{align}\] car le coefficient devant \(u_k\) est nul.

La famille \(\{f_1',\dots,f_k'\}\) est dans l’espace engendré par \(\mathrm{Vect}(u_1,\dots,u_{k-1})\). Par hypothèse de récurrence, la famille \(\{f_1',\dots,f_k'\}\) est liée, il existe \(\alpha_1,\dots,\alpha_k\in\mathbf{K}\) non tous nuls tels que

\[\sum_{j=1}^k\alpha_jf'_j=0\] Ce qui donne

\[\alpha_1f_1+\dots+\alpha_kf_k-\left(\sum_{j=1}^k\alpha_j\frac{a_{k,j}}{a_{k,k+1}}\right)f_{k+1}=0.\] Comme cette combinaison linéaire n’est pas triviale, la famille \(\{f_1,\dots,f_{k+1}\}\) est liée.

Par principe de récurrence, le résultat est assuré pour tout \(k\in\mathbf{N}\).

Corollaire 1.1 Deux bases d’un même sous-espace vectoriel ont même nombre d’éléments.

Preuve. Soit \((u_1,\dots,u_k)\) et \((v_1,\dots,v_l)\) deux bases d’un même espace vectoriel. Comme \(\{u_1,\dots,u_k\}\) est génératrice et \(\{v_1,\dots,v_l\}\) est libre, la Proposition 1.3 montre que \(l\leq k\). En échangeant les rôles des deux bases, on obtient \(k\leq l\) et donc \(k=l\).

1.5 Dimension

Le corollaire précédent nous permet de définir la dimension d’un espace vectoriel à partir de n’importe quelle base.

Définition 1.13 La dimension d’un sous-espace vectoriel est le cardinal d’une base de ce sous-espace vectoriel. On note ce nombre \(\dim(E)\).

Un sous-espace vectoriel de dimension 1, s’appelle une droite vectorielle et un sous-espace vectoriel de dimension 2 s’appelle un plan vectoriel.

Exemple 1.13 Voici deux exemples.

1. La dimension de l’espace \(\mathbf{K}^n\) est exactement \(n\) puisque la base canonique a \(n\) éléments.
2. Le sous-espace d’équation \(x+y+z=0\) dans \(\mathbf{R}^3\) possède pour base \((u_1,u_2)\) où \(u_1=(1,-1,0)\) et \(u_2=(0,-1,1)\). Ainsi, cet espace a pour dimension 2. C’est donc un plan vectoriel.

Lemme 1.4 Soit \(E,E'\) deux sous-espaces vectoriels de \(\mathbf{K}^n\). Si \(E\subset E'\) alors \(\dim(E)\leq \dim(E')\) et \(E=E'\) si et seulement si \(\dim(E)=\dim(E')\).

Preuve. Soit \(k=\dim(E')\) le cardinal d’une base de \(E'\). Toute base de \(E\) est une famille libre de \(E'\) et donc a un cardinal inférieur à \(k\) par la Proposition 1.3. Ce qui donne \(\dim(E)\leq \dim(E')\).

Maintenant, si \(E=E'\), on a bien sûr \(\dim(E)=\dim(E')\) et réciproquement si \(E\subseteq E'\) et \(E\neq E'\) alors il existe \(u\in E'\setminus E\). Pour toute base \(e_1,\dots,e_k\), la famille \(\{e_1,\dots,e_k,u\}\) est libre (sinon \(u\in\mathrm{Vect}(e_1,\dots,e_k)=E\)) et donc \(\dim(E')\geq \dim(E)+1>\dim(E)\). Ainsi, par contraposé, si \(\dim(E)=\dim(E')\) alors \(E=E'\).

Théorème 1.1 (Théorème de la base incomplète) Toute famille libre \((u_1,\dots, u_k)\) d’un sous-espace vectoriel \(E\) peut être complétée par des éléments de \(E\) en une base de \(E\) : il existe \(u_{k+1},\dots,u_l\) tels que \((u_1,\dots,u_l)\) est une base de \(E\).

Preuve. Posons \(E_1=\mathrm{Vect}(u_1,\dots, u_k)\) qui est de dimension \(k\) et \(n=\dim(E)\). Si \(E_1\neq E\) alors il existe \(u_{k+1}\in E\setminus E_1\). La famille \((u_1,\dots,u_k,u_{k+1})\) est libre et donc \(E_2=\mathrm{Vect}(u_1,\dots, u_k,u_{k+1})\) est de dimension \(k+1\). On réitère l’opération et on construit \(E_1,E_2,E_3,\dots, E_{n-k+1}\) en choisissant un vecteur \(u_l\in E\setminus E_{l-k}\) à chaque étape. Ainsi, la dimension de \(E_j\) augmente de 1 exactement à chaque étape et donc \(\dim(E_{n-k+1})=n\). Par le Lemme 1.4, on a \(E_{n-k+1}=E\). Ce qui montre que \((u_1,\dots, u_n)\) est une base de \(E\).

Théorème 1.2 Soit \(E\) un sous-espace vectoriel. De toute famille génératrice \(F\), on peut extraire une base : il existe \(u_1,\dots,u_k\in F\) tels que \((u_1,\dots, u_k)\) est une base de \(E\).

Preuve. Le sous-espace vectoriel \(E\) est un sous-espace d’un certain \(\mathbf{K}^n\). Toute famille libre dans \(F\) est de cardinal au plus \(n\) par la Proposition 1.3. On choisit une famille libre \(\{e_1,\dots,e_k\}\) de cardinal maximal dans \(F\). Cette famille est génératrice. En effet, s’il existait \(u\in E\) qui ne soit pas dans \(\mathrm{Vect}(e_1,\dots,e_k)\) alors \(\{e_1,\dots,e_k,u\}\) serait libre contredisant la maximalité de \(\{e_1,\dots,e_k\}\). Ainsi, il existe \(\alpha_1,\dots,\alpha_{k+1}\in\mathbf{K}\) tels que

\[\alpha_1 e_1+\dots+\alpha_k e_k+\alpha_{k+1}u=0.\]

Comme \(\{e_1,\dots,e_k\}\) est libre, nécessairement \(\alpha_{k+1}\neq0\). Ainsi \(u=-\frac{1}{\alpha_{k+1}}(\alpha_1 e_1+\dots+\alpha_k e_k)\in\mathrm{Vect}(e_1,\dots,e_k)\). Ce qui montre que \(\{e_1,\dots,e_k\}\) est génératrice et est donc une base.

Corollaire 1.2 Tout sous-espace vectoriel possède au moins une base. En particulier, chaque sous-espace vectoriel a une dimension bien fixée.

Preuve. Ce corollaire peut se démontrer à partir de l’un ou de l’autre des deux théorèmes ci-dessus.On utilise le Théorème 1.2. Soit \(E\) un sous-espace vectoriel. Comme l’ensemble \(E\) tout entier est une famille génératrice de lui-même, on peut en extraire une base de \(E\).

1.6 Exercices

Exercice 1.1 Vérifier que \(\mathbf{F}_2\) avec les tables d’addition et de multiplication données est bien un corps.

Exercice 1.2 Dans \(\mathbf{F}_2\), on identifie \(0\) à la valeur booléenne FAUX et \(1\) à la valeur booléenne VRAI. Montrer que \(xy\) correspond à l’opération booléenne “\(x\) et \(y\)” alors que \(x+y+xy\) correspond à l’opération “\(x\) ou \(y\)”. À quelle opération booléenne correspond l’addition \(x+y\) ?

Exercice 1.3 La réunion de deux sous-espaces vectoriels \(E_1\) et \(E_2\) est-elle un sous-espace vectoriel ? Vous pourrez réfléchir à l’exemple donné par \(E_1=\{(x,y)\in\mathbf{R}^2,\ x+y=0\}\) et \(E_2=\{(x,y)\in\mathbf{R}^2,\ x-y=0\}\) en les dessinant.

Exercice 1.4 Les familles suivantes forment-elles des familles libres, génératrices de \(\mathbf{R}^n\) ? Sont-elles des bases de \(\mathbf{R}^n\) ?

1. \(\begin{bmatrix}1\\2\end{bmatrix}\) et \(\begin{bmatrix}1\\3\end{bmatrix}\) dans \(\mathbf{R}^2\).
2. \(\begin{bmatrix}1\\2\end{bmatrix}\) et \(\begin{bmatrix}3\\6\end{bmatrix}\) dans \(\mathbf{R}^2\).
3. \(\begin{bmatrix}1\\2\end{bmatrix}\), \(\begin{bmatrix}3\\5\end{bmatrix}\) et \(\begin{bmatrix}4\\2\end{bmatrix}\) dans \(\mathbf{R}^2\).
4. \(\begin{bmatrix}1\\2\\3\end{bmatrix}\) et \(\begin{bmatrix}4\\5\\6\end{bmatrix}\) dans \(\mathbf{R}^3\).
5. \(\begin{bmatrix}1\\2\\3\end{bmatrix}\), \(\begin{bmatrix}5\\7\\9\end{bmatrix}\) et \(\begin{bmatrix}4\\5\\6\end{bmatrix}\) dans \(\mathbf{R}^3\).
6. \(\begin{bmatrix}1\\2\\3\end{bmatrix}\), \(\begin{bmatrix}5\\7\\9\end{bmatrix}\) et \(\begin{bmatrix}7\\11\\13\end{bmatrix}\) dans \(\mathbf{R}^3\).

Exercice 1.5 On considère les vecteurs \(e_1=\begin{bmatrix}1\\1\\1\end{bmatrix}\) et \(e_2=\begin{bmatrix}1\\-1\\1\end{bmatrix}\)

1. Montrer qu’ils forment une famille libre de \(\mathbf{R}^3\).
2. Représenter le sous-espace vectoriel engendré par ces vecteurs.
3. Compléter cette famille en une base \((e_1,e_2,e_3)\) de \(\mathbf{R}^3\).

Exercice 1.6 On considère \(u_1=\begin{bmatrix}1\\2\\3\end{bmatrix}\), \(u_2=\begin{bmatrix}5\\7\\9\end{bmatrix}\) et \(u_3=\begin{bmatrix}4\\5\\6\end{bmatrix}\) dans \(\mathbf{R}^3\). Soit \(V\) le sous-espace vectoriel engendré par ces vecteurs.

1. Extraire une base de \(V\) dans la famille \((u_1,u_2,u_3)\).
2. Quelle est la dimension de \(V\) ?
3. Trouver une équation linéaire pour \(V\), c’est-à-dire, trouver des coefficients \(a,b,c\in\mathbf{R}^3\) tels que \[\begin{bmatrix}x\\y\\z\end{bmatrix}\in V\iff ax+by+cz=0.\]

Exercice 1.7 On considère les vecteurs \(\begin{bmatrix}1\\1\end{bmatrix}\) et \(\begin{bmatrix}1\\-1\end{bmatrix}\).

1. Montrer que ces vecteurs forment une base de \(\mathbf{R}^2\)
2. Quelles sont les coordonnées des vecteurs \(\begin{bmatrix}1\\2\end{bmatrix}\) et \(\begin{bmatrix}5\\7\end{bmatrix}\) dans cette base ?
3. Représenter géométriquement les coordonnées de ces vecteurs avec des parallélogrammes dans le plan \(\mathbf{R}^2\).

Exercice 1.8 On considère les vecteurs les vecteurs \(\begin{bmatrix}1\\1\end{bmatrix}\) et \(\begin{bmatrix}1\\0\end{bmatrix}\).

1. Montrer que ces vecteurs forment une base de \(\mathbf{F}_2^2\).
2. Quelles sont les coordonnées du vecteur \(\begin{bmatrix}0\\1\end{bmatrix}\) dans cette base ?

Exercice 1.9 Soit \(\mathbf{K}\) un corps.

1. Montrer que toute famille libre de \(\mathbf{K}^n\) a au plus \(n\) éléments.
2. Montrer que toute famille génératrice de \(\mathbf{K}^n\) a au moins \(n\) éléments.
3. Montrer que toute famille libre de \(\mathbf{K}^n\) est une base si et seulement si elle a exactement \(n\) éléments.
4. Montrer que toute famille génératrice de \(\mathbf{K}^n\) est une base si et seulement si elle a exactement \(n\) éléments.

Exercice 1.10 On considère le corps \(\mathbf{K}=\mathbf{F}_2\). Quel est le cardinal d’un sous-espace vectoriel de dimension \(n\) ?

Exercice 1.11 Montrer que les ensembles suivants sont des sous-espaces vectoriels de \(\mathbf{R}^3\).

1. \(E_2=\{(x,y,z)\in \mathbb{R}^{3}\mid 3x-7y=z\}\). En déterminer une base et sa dimension.
2. \(E_{3}=\{(x,y,z)\in\mathbb{R}^{3}\mid x+y-z=0 \quad \mathrm{et}\quad x+y+z=0\}\). En déterminer une base et sa dimension.

Exercice 1.12 On considère deux plans dans \(\mathbf{R}^{3}\): \[P_{1}=\{(x,y,z)\in\mathbf{R}^{3}\mid x-y+z=0\}\] \[P_{2}=\{(x,y,z)\in\mathbf{R}^{3}\mid x-y=0\}\] Trouver une base \(P_{1}\cap P_{2}\). Quelle est sa dimension?

Exercice 1.13 Soit \(n\in\mathbf{N}\). On note \(\mathcal{P}_n\) pour l’ensemble des polynômes de degrés au plus \(n\). On identifie le polynôme \(a_{n}X^n+\dots+a_1X+a_0\) avec le vecteur \((a_0,\dots,a_n)\in\mathbf{R}^{n+1}\).

1. Si \(P=a_{n}X^n+\dots+a_1X+a_0\) et \(Q=b_{n}X^n+\dots+b_1X+b_0\), a quel vecteur correspond le polynôme \(P+Q\) ?
2. Même question pour le polynôme \(\lambda P\) où \(\lambda\in\mathbf{R}\).
3. À quelle famille de polynômes correspond la base canonique de \(\mathbf{R}^{n+1}\) ?
4. Montrer que l’ensemble \(E_1=\{P\in\mathcal{P}_n,\ P(1)=0\}\) est un sous-espace vectoriel de \(\mathcal{P}_n\).
5. Pour chaque \(k\leq n\), trouver un polynôme \(P_k\) de degré \(k\) tel que \(P_k\in E_1\).
6. Donner une base de \(E_1\) et en déduire sa dimension.