Chapitre 4 Orthogonalité

4.1 Produit scalaire, norme et distance euclidiennes

Définition 4.1 (transposée) Soit \(A\in\mathrm{M}_{m,n}(\mathbf{R})\), la transposée de \(A\) est la matrice \(^tA\in\mathrm{M}_{n,m}(\mathbf{R})\) donnée par

\[(^tA)_{i,j}=A_{j,i}\]

pour tout \(1\leq i\leq n\) et \(1\leq j\leq m\).

Remarque. La transposition correspond à échanger les lignes avec les colonnes.

Exemple 4.1 La transposée d’un vecteur colonne \(X=\begin{bmatrix}X_1\\\dots\\X_n\end{bmatrix}\) est le vecteur ligne \(^tX=\begin{bmatrix}X_1,\dots,X_n\end{bmatrix}\).

Exemple 4.2 La transposée de la matrice

\[A=\begin{bmatrix}1&0&2\\3&2&1\end{bmatrix}\] est la matrice

\[^tA=\begin{bmatrix}1&3\\0&2\\2&1\end{bmatrix}.\]

Proposition 4.1 Si \(A\in\mathrm{M}_{n,m}(\mathbf{K})\) et \(B\in\mathrm{M}_{m,l}(\mathbf{K})\) alors \(^t(AB)=(^tB)(^tA)\).

Preuve. Le coefficient d’indice \((i,j)\) de \(AB\) est \(\sum_{k=1}^mA_{i,k}B_{k,j}\) donc le coefficient d’indice \((i,j)\) de \(^t(AB)\) est \(\sum_{k=1}^mA_{j,k}B_{k,i}\).

Le coefficient de \((^tB)(^tA)\) d’indice \((i,j)\) est

\[\begin{align*} \sum_{k=1}^m (^tB)_{i,k} (^tA)_{k,j} &=\sum_{k=1}^m B_{k,i}A_{j,k}\\ &=\sum_{k=1}^m A_{j,k}B_{k,i}. \end{align*}\]

Les matrices \(^t(AB)\) et \((^tB)(^tA)\) ont même coefficients, elles sont donc égales.

Définition 4.2 (produit scalaire) Soit \(u,v\) deux vecteurs de \(\mathbf{R}^n\), le produit scalaire de \(u\) et \(v\) est le nombre réel

\[\langle u,v\rangle=\sum_{i=1}^nu_iv_i\]

où \((u_i)\) et \((v_i)\) sont les coordonnées de \(u\) et \(v\) dans la base canonique.

Remarque. Si \(X\) et \(Y\) sont des vecteurs colonnes de \(\mathbf{R}^n\) alors \(\langle X,Y\rangle\) s’identifie avec la matrice de taille \(1\times 1\) \[^tXY.\]

Proposition 4.2 Pour tout \(u,v,w\in\mathbf{R}^n\) et \(\lambda\in \mathbf{R}\), on a les propriétés suivantes :

• \(\langle u,v\rangle=\langle v,u\rangle\),
• \(\langle u+v,w\rangle=\langle u,w\rangle+\langle v,w\rangle\),
• \(\langle \lambda u,v\rangle=\lambda \langle u,v\rangle\),
• \(\langle u,u\rangle\geq 0\),
• \(\langle u,u\rangle= 0\iff u=0\).

Preuve. On prouve les propriétés les unes à la suite des autres.

• \(\langle u,v\rangle=\sum_{i=1}^nu_iv_i=\sum_{i=1}^nv_iu_i=\langle v,u\rangle\),
• \(\langle u+v,w\rangle=\sum_{i=1}^n(u_i+v_i)w_i=\sum_{i=1}^nu_iw_i+\sum_{i=1}^nv_iw_i=\langle u,w\rangle+\langle v,w\rangle\),
• \(\langle \lambda u,v\rangle=\sum_{i=1}^n\lambda u_iv_i=\lambda\sum_{i=1}^nu_iv_i=\lambda \langle u,v\rangle\)
• \(\langle u,u\rangle=\sum_{i=1}^nu_i^2\geq0\),
• \(\langle u,u\rangle=\sum_{i=1}^nu_i^2=0\iff\forall i,\ u_i=0\iff u=0\).

Définition 4.3 (norme euclidienne) Soit \(u\in \mathbf{R}^n\), la norme euclidienne (ou simplement norme) de \(u\) est le réel positif

\[||u||=\sqrt{\langle u,u\rangle}=\sqrt{\sum_{i=1}^nu_i^2}.\]

Remarque. La dernière propriété de la Proposition 4.2 montre que \(||u||=0\iff u=0\).

Définition 4.4 (distance euclidienne) Soit \(u,v\in\mathbf{R}^n\), la distance euclidienne (ou simplement distance) entre \(u\) et \(v\) est le nombre réel positif

\[d(u,v)=||u-v||=\sqrt{\sum_{i=1}^n(u_i-v_i)^2}.\]

Remarque. La norme \(||u||\) d’un vecteur \(u\) est donc la distance de \(u\) à 0.

4.2 Orthogonalité

Définition 4.5 Soit \(u,v\) deux vecteurs de \(\mathbf{R}^n\). Ils sont orthogonaux si \(\langle u,v\rangle=0\).

On note alors \(u\bot v\).

Exemple 4.3 Si \(u=\begin{bmatrix}1\\1\end{bmatrix}\) et \(\begin{bmatrix}1\\-1\end{bmatrix}\) alors \(u\) et \(v\) sont orthogonaux car \(\langle u,v\rangle =1-1=0\).

Exemple 4.4 Les vecteurs \(e_1,\dots, e_n\) de la base canonique sont orthogonaux car \(\langle e_i,e_j\rangle=1\) si \(i=j\) et \(\langle e_i,e_j\rangle=0\) si \(i\neq j\).

Définition 4.6 Soit \(E\) un sous-ensemble de \(\mathbf{R}^n\). L’orthogonal de \(E\) est l’ensemble

\[\{y\in\mathbf{R}^n,\ \forall x\in E,\ \langle x,y\rangle=0\}.\] On le note \(E^\bot\). Si \(u\in E^\bot\), on note aussi \(u\bot E\).

Lemme 4.1 L’ensemble \(E^\bot\) est un sous-espace vectoriel de \(\mathbf{R}^n\).

Preuve. Soit \(y_1,y_2\in E^\bot\), pour tout \(x\in E\), \(\langle y_1+y_2,x\rangle=\langle y_1,x\rangle+\langle y_2,x\rangle=0\) et donc \(y_1+y_2\in E^\bot\). Si \(y\in E^\bot\) et \(\lambda\in \mathbf{R}\), \(\langle\lambda y,x\rangle=\lambda\langle y,x\rangle=0\) et donc \(\lambda x\in E^\bot\).

Définition 4.7 Une famille \(F=\{u_1,\dots,u_k\}\) est \(orthogonale\) si pour tout \(i,j\), \(u_i\bot u_j\).

Lemme 4.2 Soit \(F\) une famille orthogonale de vecteurs tous non nuls. Alors \(F\) est libre.

Preuve. Soit \(u_1,\dots,u_k\in F\) et \(\lambda_1,\dots,\lambda_k\in\mathbf{R}\) tels que \[\lambda_1u_1+\dots+\lambda_ku_k=0.\] On veut montrer que \(\lambda_1=\dots=\lambda_k=0\). Posons \(v=\lambda_1u_1+\dots+\lambda_ku_k\) et calculons \(\langle v,u_i\rangle\). Comme \(v=0\), \(\langle v,u\rangle=0\) et par linéarité \(\langle v,u_i\rangle=\sum_{j=1}^k\lambda_j\langle u_j,u_i\rangle=\lambda_i\langle u_i,u_i\rangle\) pour un \(i\) fixée. Comme \(u_i\neq 0\), \(\langle u_i,u_i\rangle\neq 0\) et donc \(\lambda_i=0\). Ce qui montre que la famille est libre.

Définition 4.8 Une base \(\mathcal{B}=(u_1,\dots,u_n)\) de \(\mathbf{R}^n\) est orthonormée si pour tout \(i\neq j\), \(u_i\bot u_j\) et \(||u_i||=1\) pour tout \(i\in\{1,\dots,n\}\).

Remarque. Par le Lemme 4.2, une famille orthogonale avec \(n\) vecteurs de norme 1 est automatiquement une base orthonormée.

Exemple 4.5 La base canonique est une base orthonormée.

Exemple 4.6 La famille \(u_1=\frac{1}{\sqrt{2}}\begin{bmatrix}1\\1\end{bmatrix}\) et \(u_2\frac{1}{\sqrt{2}}\begin{bmatrix}-1\\1\end{bmatrix}\) est une base orthonormée car \(||u_1||=||u_2||=1\) et \(u_1\bot u_2\).

4.3 Projections et point le plus proche

Définition 4.9 Soit \(u\) un vecteur de \(\mathbf{R}^n\) et \(D\) la droite engendrée par \(u\). La projection d’un vecteur \(v\in\mathbf{R}^n\) sur \(D\) est le vecteur \(\frac{\langle u,v\rangle}{\langle u,u\rangle}u\). On le note \(P_D(v)\).

Définition 4.10 Soit \(E\) un sous-espace vectoriel de \(\mathbf{R}^n\) et \(u_1,\dots,u_k\) une base orthonormée de \(E\). La projection d’un vecteur \(v\) sur \(E\) est le vecteur \(P_E(v)=\sum_{i=1}^k\langle v,u_i\rangle u_i\in E\).

Remarque. Il s’agit donc de la somme des projections sur les droites engendrées par les \(u_i\).

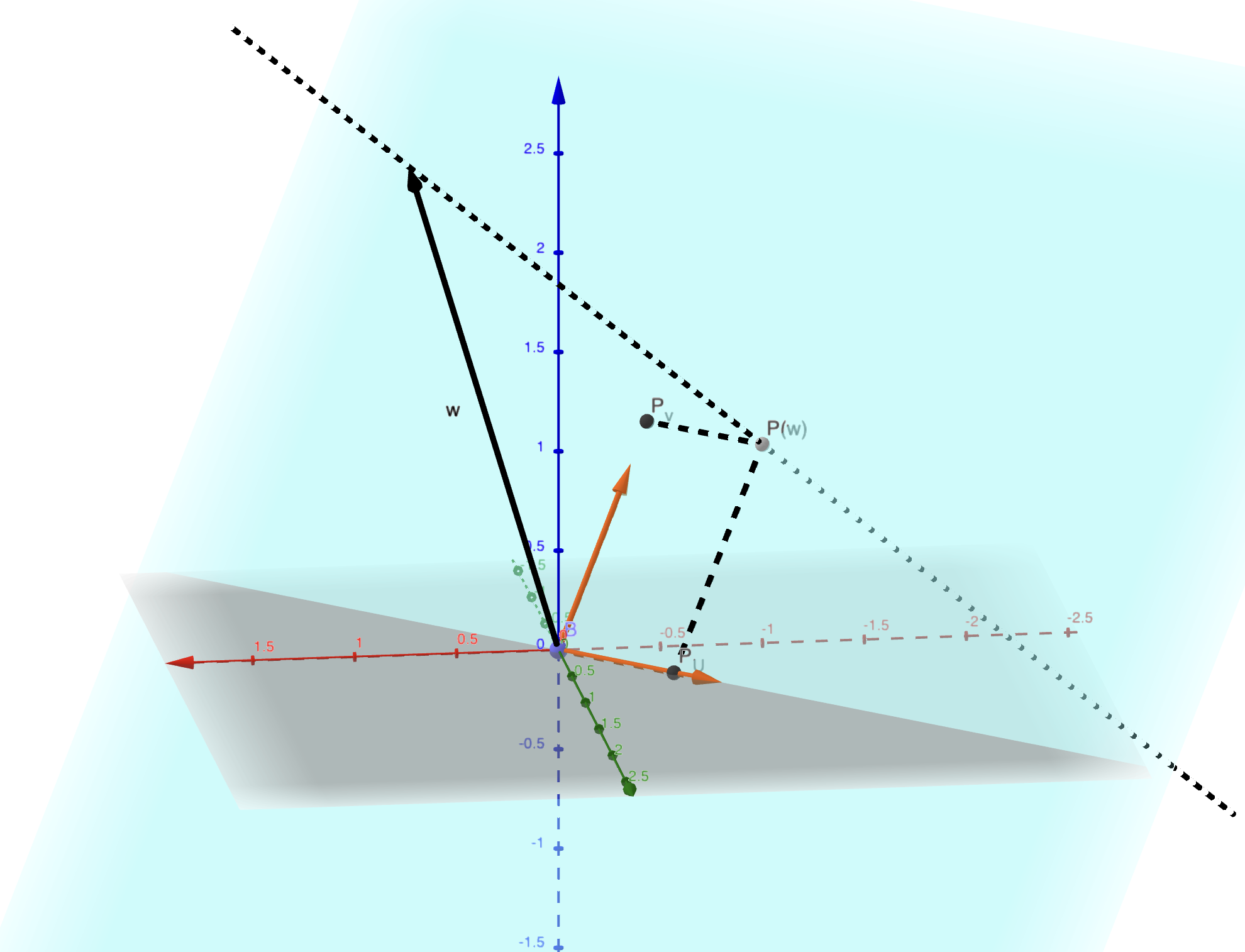
Figure 4.1: La projection du vecteur w sur un plan.

Lemme 4.3 Soit \(E\) un sous-espace vectoriel de \(\mathbf{R}^n\). L’application \(u\mapsto P_E(u)\) est une application linéaire.

Preuve. Soit \(v_1,v_2\in\mathbf{R}^n\). Alors

\[\begin{align*} P_E(v_1+v_2)&=\sum_{i=1}^k\langle v_1+v_2,u_i\rangle u_i\\ &=\sum_{i=1}^k\langle v_1,u_i\rangle u_i+\sum_{i=1}^k\langle v_2,u_i\rangle u_i\\ &=P_E(v_1)+P_E(v_2) \end{align*}\]

Pour \(\lambda\in\mathbf{R}\) et \(v\in\mathrm{R}^n\),

\[\begin{align*} P_E(\lambda v)&=\sum_{i=1}^k\langle \lambda v,u_i\rangle u_i\\ &=\lambda\sum_{i=1}^k\langle v,u_i\rangle u_i\\ &=\lambda P_E(v) \end{align*}\]

Donc la projection orthogonale sur \(E\) est bien une application linéaire.

Lemme 4.4 Soit \(E\) un sous-espace vectoriel de \(\mathbf{R}^n\) et \(v\in\mathbf{R}^n\). Alors \(v-P_E(v)\in E^\bot\) et

\[||v||^2=||P_E(v)||^2+||v-P_E(v)||^2.\]

Preuve. Posons \(v_\bot=v-P_E(v)\). Alors \(v=P_E(v)+v_\bot\).

Pour \(i\in\{1,\dots,k\}\),

\[\begin{align*}\langle u_i,v_\bot\rangle=&\langle v,u_i\rangle-\langle P_E(v),u_i\rangle\\ &=\langle v,u_i\rangle-\sum_{l=1}^k\langle \langle v,u_l\rangle u_l,u_i\rangle\\ &=\langle v,u_i\rangle-\sum_{l=1}^k\langle v,u_l\rangle\langle u_l,u_i\rangle\\ &=\langle v,u_i\rangle-\langle v,u_i\rangle\langle u_i,u_i\rangle\\ &=\langle v,u_i\rangle-\langle v,u_i\rangle\\ &=0 \end{align*}\]

Ainsi, on a bien que \(v_\bot=v-P_E(v)\in E^\bot\).

Maintenant,

\[\begin{align*} ||v||^2&=\langle v,v\rangle\\ &=\langle P_E(v)+v_\bot,P_E(v)+v_\bot\rangle\\ &=\langle P_E(v),P_E(v)\rangle +\langle v_\bot,P_E(v)\rangle+\langle P_E(v), v_\bot\rangle+\langle v_\bot,v_\bot\rangle\\ &=\langle P_E(v),P_E(v)\rangle+\langle v_\bot,v_\bot\rangle\\ &=||P_E(v)||^2+||v-P_E(v)||^2. \end{align*}\]

Lemme 4.5 (Inégalité de Cauchy-Schwarz) Soit \(u,v\in\mathbf{R}^n\) alors

\[|\langle u,v\rangle|\leq ||u||||v||.\]

Preuve. Par construction, on a \(\langle u,v\rangle=\langle P_D(u),v\rangle\) où \(D\) est la droite engendrée par \(v\).

Or \(P_D(u)=||P_D(u)|| \frac{v}{||v||}\) si \(P_D(u)\) et \(v\) ont même sens et sinon \(P_D(u)=-||P_D(u)|| \frac{v}{||v||}\). Ainsi

\(|\langle P_D(u),v\rangle|=||P_D(u)||\times||v||^2/||v||=||P_D(u)||\times||v||\) et comme \(||P_D(u)||\leq ||u||\), on a le résultat.

Proposition 4.3 (Inégalité triangulaire) Soit \(u,v\in\mathbf{R}^n\) alors

\[||u+v||\leq ||u||+||v||.\]

Remarque. Soit \(a,b,c\) trois points de \(\mathbf{R}^n\), en prenant \(u=a-b\) et \(v=b-c\) dans la proposition précédente, on obtient

\[d(a,c)\leq d(a,b)+d(b,c).\]

Preuve. On calcule \(||u+v||^2\) :

\[\begin{align*} ||u+v||^2&=\langle u+v,u+v\rangle\\ &=||u||^2+2\langle u,v\rangle+||v||^2\\ &\leq ||u||^2+2||u||||v||+||v||^2\\ &\leq (||u||+||v||)^2 \end{align*}\]

Ainsi, \(||u+v||\leq ||u||+||v||.\)

Proposition 4.4 Soit \(E\) un sous-espace vectoriel de \(\mathbf{R}^n\) et \(u\in\mathbf{R}^n\). Alors pour tout \(v\in E\)

\[||u-v||\geq||u-P_E(u)||.\]

Remarque. Cela signifie que \(P_E(u)\) est le point de \(E\) le plus proche de \(u\). En particulier, ce point \(P_E(u)\) ne dépend pas du choix de la base orthonormée choisie pour le définir.

Définition 4.11 (Orthogonalisation de Gram-Schmidt) Soit \(u_1,\dots,u_k\) une base d’un sous-espace vectoriel \(F\) de \(\mathbf{R}^n\). On définit par récurrence les vecteurs

\[\begin{align*} v_1&=u_1\\ v_2&=u_2-\frac{\langle u_2,v_1\rangle}{\langle v_1,v_1\rangle}v_1\\ v_3&=u_3-\frac{\langle u_3,v_1\rangle}{\langle v_1,v_1\rangle}v_1-\frac{\langle u_3,u_v\rangle}{\langle v_2,v_2\rangle}v_2\\ \vdots&=\vdots\\ v_k&=u_k-\frac{\langle u_k,v_1\rangle}{\langle v_1,v_1\rangle}v_1-\dots-\frac{\langle u_k,v_{k-1}\rangle}{\langle v_{k-1},v_{k-1}\rangle}v_{k-1}\\ \end{align*}\]

Finalement, on pose \(e_i=\frac{v_i}{||v_i||}\).

Théorème 4.1 La famille \((e_1,\dots,e_k)\) est une base orthonormée de \(F\).

Preuve. On montrer par récurrence sur \(i=1,\dots,k\) que \((e_1,\dots,e_i)\) est une base orthonormée de \(\mathrm{Vect}(e_1,\dots,e_i)\).

Cas \(k=1\) : \(e_1\) est non nul et de norme 1.

Étape de de réccurence: On suppose le résultat pour \(k-1\). Il reste alors à montrer que \(e_k\bot e_i\) pour \(i<k\) car \(||e_k||=1\), ce qui est équivalent à \(v_k\bot v_i\) pour \(i<k\). On calcule \(\langle v_k,v_i\rangle=\langle u_k,v_i\rangle-\frac{\langle u_k,v_i\rangle}{\langle v_i,v_i\rangle}\langle v_i,v_i\rangle=0\).

Exemple 4.7 Soit \(F\) le plan d’équation \(x+y+z=0\) et \(v=(1,2,3)\). On veut calculer la projection orthogonale de \(v\) sur \(F\). On commence par calculer une base orthonormée pour cela. Les vecteurs \(u_1=(1,-1,0)\) et \(u_2=(0,1,-1)\) forment une base de \(F\).

On applique le procédé d’orthonormalisation de Gram-Schmidt et on obtient \(v_1=u_1\) et \(e_1=(\frac{1}{\sqrt{2}},\frac{-1}{\sqrt{2}},0)\) puis \(v_2=u_2+\frac{1}{2}u_1=(1/2,1/2,-1)\) et finalement \(e_2=\sqrt{2/3}\left(1/2,1/2,-1\right)=\left(1/\sqrt{6},1/\sqrt{6},-2/\sqrt{6}\right)\).

Comme \(\langle v,e_1\rangle=-1/\sqrt{2}\) et \(\langle v,e_2\rangle=-3/\sqrt{6}\), on obtient que

\[\begin{align*} P_F(v)&=\frac{-1}{\sqrt{2}}e_1-\frac{3}{\sqrt{6}}e_2\\ &=(-1,0,1). \end{align*}\]

4.4 Matrices orthogonales

Définition 4.12 (Matrice orthogonale) Soit \(A\in\mathrm{M}_n(\mathbf{R})\). La matrice \(A\) est orthogonale si \(^tAA=I_n\).

Lemme 4.6 Soit \(A\in\mathrm{M}_n(\mathbf{R})\). Notons \(A_1,\dots,A_n\) les vecteurs colonnes de la matrice \(A\). Soit \(P\) la matrice \(^tAA\). Le coefficient d’indice \((i,j)\) de \(P\) est \(\langle A_i, A_j\rangle\).

Preuve. Notons \(B=^tA\). Par définition du produit matriciel, le coefficient \(P_{i,j}\) de \(P\) est \(\sum_{k=1}^nB_{i,k}A_{k,j}\). Comme \(B_{i,k}=A_{k,i}\), \(P_{i,j}=\sum_{k=1}^nA_{k,i}A_{k,j}=\langle A_i,A_j\rangle\).

Proposition 4.5 Une matrice \(A\) est orthogonale si et seulement si \(A\) est inversible d’inverse \(^tA\) si seulement si les colonnes de \(A\) forment une base orthonormée.

Preuve. L’équation matricielle \(^tAA=I_n\) signifie exactement que \(^tA\) est l’inverse de \(A\).

Par le Lemme 4.6, Posons \(P=^tAA\). Ainsi, le coefficient \(P_{i,j}\) est \(\langle A_i,A_j\rangle\). Ainsi, \[P=I_n\iff \left\{\begin{matrix}\langle A_i,A_j\rangle=0,\ \textrm{pour}\ i\neq j\\ \langle A_i,A_j\rangle=1,\ \textrm{pour}\ i=j \end{matrix}\right. .\] Ce qui siginifie exactement que la famille des colonnes de la matrice \(A\) est une base orthonormée.

Remarque. Une matrice orthogonale correspond alors exactement à une matrice de passage, de la base canonique vers une base orthonormée.

Exemple 4.8 Voici quelques exemples.

1. La matrice \(\frac{1}{\sqrt{2}}\begin{bmatrix}1&-1\\1&1\end{bmatrix}\) est une matrice orthogonale en dimension 2.
2. La matrice \(\begin{bmatrix}0&1&0\\0&0&1\\1&0&0\end{bmatrix}\) est orthogonale en dimension 3.
3. La matrice \(\frac{1}{9}\begin{bmatrix}-8&4&1\\4&7&4\\1&4&-8\end{bmatrix}\) est orthogonale en dimension 3.

Proposition 4.6 Soit \(A\) une matrice orthogonale de \(\mathbf{R}^n\). Pour tout vecteur \(X,Y\in\mathbf{R}^n\), on a

\[\langle AX,AY\rangle=\langle X,Y\rangle.\]

Preuve. On a \(\langle AX,AY\rangle=^t(AX)AY=^tX^tAAY=^tXY=\langle X,Y\rangle.\)

Corollaire 4.1 Les changements de bases orthonormées préservent l’orthogonalité, les normes et les distances : Pour tout \(X,y\in\mathbf{R}^n\) et \(A\) matrice orthogonale :

1. \(X\bot Y\iff AX\bot AY\),
2. \(||AX||=||X||\) et
3. \(d(AX,AY)=d(X,Y)\).

Preuve. On a

1. \(X\bot Y\iff \langle X,Y\rangle=0\iff \langle AX,AY\rangle=0\iff AX\bot AY\),
2. \(||AX||^2=\langle AX,AX\rangle=\langle X,X \rangle=||X||^2\) et
3. \(d(AX,AY)=||AX-AY||=||A(X-Y)||=||X-Y||=d(X,Y).\)

4.5 Exercices

Exercice 4.1 (Théorème de Pythagore) Soit \(u,v\in\mathbf{R}^n\).

1. Montrer que \(||u+v||^2=||u||^2+2\langle u,v\rangle+||v||^2\).
2. En déduire que \(u\bot v\iff ||u+v||^2=||u||^2+||v||^2\).
3. Quel est le lien avec le théorème de Pythagore ?

Exercice 4.2 On considère les vecteurs \(u_1=(1,0,1)\), \(u_2=(1,1,1)\) et \(u_3=(-1,1,0)\). Appliquer le procédé de Gram-Schmidt à la famille \((u_1,u_2,u_3)\) .

Exercice 4.3 Dans \(\mathbf{R}^3\), on considère les vecteurs \(v_1=(1,1,0)\) et \(v_2=(1,1,1)\). Soit \(F=\mathrm{Vect}(v_1,v_2)\).

1. Trouver une base orthonormée pour \(F\) à l’aide du procédé d’orthonormalisation de Gram-Schmidt.
2. Calculer l’image des vecteurs de la base canonique par la projection orthogonale sur \(F\), notée \(P_F\).
3. En déduire la matrice de \(P_F\) dans la base canonique.
4. Donner un système d’équations définissant \(F^\bot\).
5. Donner une base orthonormée de \(F^\bot\).
6. Quelle est la distance du vecteur \((1,-1,1)\) à \(F\) ?

Exercice 4.4 Vérifier que la matrice \(A=\frac{-1}{3}\begin{bmatrix}-2&1&2\\2&2&1\\1&-2&2\end{bmatrix}\) est une matrice orthogonale.

Exercice 4.5 Dans \(\mathbf{R}^3\), on considère le point \(C=(1,2,1)\).

1. Donner une équation pour la sphère \(S\) de centre \(C\) et de rayon 2, c’est-à-dire l’ensemble des points à distance 2 de \(C\).
2. Donner une équation pour \(C^\bot\). Quelle est la dimension de ce sous-espace ? En donner une base orthonormée.
3. Représenter avec \(S\) et \(C^\bot\) avec Geogebra 3D.
4. Justifier que \(C^\bot\cap S=\emptyset\).

Exercice 4.6 Soit \(\mathcal{B}=(u_1,\dots,u_n)\) une base de \(\mathbf{R}^n\) et \(\mathcal{B}'=(e_1,\dots,e_n)\) la base orthonormée obtenue par le procédé de Gram-Schmidt. On note \(R\) la matrice de passage de \(\mathcal{B}'\) à \(\mathcal{B}\).

1. Donner les coefficients de \(R\).
2. Observer que \(R\) est triangulaire supérieure.
3. Soit \(Q\) la matrice de passage de la base canonique \(\mathcal{B}_0\) à \(\mathcal{B}'\). Justifier que \(Q\) est une matrice orthogonale.
4. Soit \(A\) une matrice inversible de \(\mathrm{M}_n(\mathbf{R})\). On note \(u_1,\dots, u_n\) ces vecteurs colonne. En interprétant \(A\) comme la matrice de passage de la base \(\mathcal{B}_0\) à \(\mathcal{B}\), justifier que \(A=QR\).
5. Justifier que la solution d’un système linéaire \(AX=B\) où \(X\in\mathbf{R}^n\) est l’inconnue et \(B\in\mathbf{R}^n\) est donnée, se résoud par \(X=R^{-1}(^tQ)B\) et que cela se calcule assez facilement.