Chapter 1 Vector Spaces

1.1 Field

The concept of a field generalizes the arithmetic rules we are used to for real numbers.

Definition 1.1 (field) A field is a set \(\mathbf{K}\) equipped with two internal operations called addition “\(+\)” and multiplication “\(\times\)” that satisfy the following properties:

1. Addition is associative: \(\forall a,b,c \in \mathbf{K}\), \((a+b)+c = a+(b+c)\).
2. Addition is commutative: \(\forall a,b \in \mathbf{K}\), \(a+b = b+a\).
3. Multiplication is associative: \(\forall a,b,c \in \mathbf{K}\), \((a \times b) \times c = a \times (b \times c)\).
4. Multiplication is commutative: \(\forall a,b \in \mathbf{K}\), \(a \times b = b \times a\).
5. Multiplication is distributive over addition: \(\forall a,b,c \in \mathbf{K}\), \(a \times (b + c) = (a \times b) + (a \times c)\).
6. There exists an element denoted \(0\) such that for all \(a \in \mathbf{K}\), \(a + 0 = a\) and \(a \times 0 = 0\).
7. There exists an element denoted \(1\) such that for all \(a \in \mathbf{K}\), \(a \times 1 = a\).
8. Every element has an additive inverse: \(\forall a \in \mathbf{K}\), \(\exists b \in \mathbf{K}\) such that \(a + b = 0\). We denote the additive inverse of \(a\) by \(-a\).
9. Every non-zero element has a multiplicative inverse: \(\forall a \in \mathbf{K} \setminus \{0\}\), \(\exists b \in \mathbf{K}\) such that \(a \times b = 1\).

Example 1.1 The first example is the set of real numbers \(\mathbf{R}\).

Example 1.2 The set of rational numbers \(\mathbf{Q}\) also forms a field. This consists of fractions \(p/q\) where \(p\) and \(q\) are integers with \(q \neq 0\).

Example 1.3 The positive real numbers \(\mathbf{R}^+\) do not form a field: no non-zero element has an additive inverse.

Example 1.4 The integers \(\mathbf{Z}\) do not form a field: numbers other than \(-1, 0\), and \(1\) do not have a multiplicative inverse. For example, the inverse of 2 should be 1/2, which is not in \(\mathbf{Z}\).

Example 1.5 The set \(\mathbf{C}\) of complex numbers forms a field.

Definition 1.2 (field with two elements) The field with two elements is \(\mathbf{F}_2 = \mathbf{Z}/2\mathbf{Z}\). It consists of the set \(\{0,1\}\) with the following addition and multiplication tables:

Addition Table

• \(0+0 = 0\)
• \(1+0 = 1\)
• \(1+1 = 0\)

Multiplication Table

• \(0 \times 1 = 0\)
• \(1 \times 1 = 1\)
• \(0 \times 0 = 0\)

Remark. The field \(\mathbf{F}_2 = \mathbf{Z}/2\mathbf{Z}\) corresponds to arithmetic modulo 2. It is often used for Boolean arithmetic where the values TRUE (corresponding to 1) and FALSE (corresponding to 0) are manipulated.

In the following sections, we will use the two fields \(\mathbf{R}\) and \(\mathbf{F}_2\).

1.2 Canonical Vector Spaces

Definition 1.3 (Canonical Vector Space) Let \(\mathbf{K}\) be a field and \(n\) be a positive integer. The canonical vector space of dimension \(n\) over \(\mathbf{K}\) is \(\mathbf{K}^n\). An element of \(\mathbf{K}^n\) is called a vector. An element of the field \(\mathbf{K}\) is called a scalar.

A vector \(v\) is thus an \(n\)-tuple \((v_1, \dots, v_n)\). The numbers \(v_i\) are the coordinates of \(v\). The vector \((0, \dots, 0)\) is called the zero vector.

Definition 1.4 (Vector Addition) Let \(x = (x_1, \dots, x_n)\) and \(y = (y_1, \dots, y_n)\) be two vectors. The sum \(x + y\) is the vector \((x_1 + y_1, \dots, x_n + y_n)\).

Definition 1.5 (Scalar Multiplication) Let \(\lambda \in \mathbf{K}\) be a scalar and \(v = (v_1, \dots, v_n)\) be a vector. The vector \(\lambda \cdot v\) is the vector \((\lambda v_1, \dots, \lambda v_n)\).

Example 1.6 The vector space \(\mathbf{F}_2^n\) corresponds to binary words of length \(n\).

Remark. There is an abstract notion of vector space over a field \(\mathbf{K}\) that we will not cover here. We will only use canonical vector spaces and their subspaces. An abstract vector space is essentially a set \(E\) with a vector addition and scalar multiplication.

Remark. Vectors can be written in either row or column format. For example, \((1,0,3)\) or \(\begin{pmatrix} 1\\ 0\\ 3\end{pmatrix}\). The choice of format is often irrelevant but will be important when performing matrix multiplications.

Remark. Vectors can be written with parentheses or brackets. This does not change the meaning. For example, \(\begin{pmatrix} 1\\ 0\\ 3\end{pmatrix}\) and \(\begin{bmatrix} 1\\ 0\\ 3\end{bmatrix}\) represent the same vector.

Proposition 1.1 The vector space \(\mathbf{K}^n\) satisfies the following properties:

1. Associativity of vector addition: \(\forall u,v,w \in \mathbf{K}^n\), \(u + (v + w) = (u + v) + w\).
2. Commutativity of vector addition: \(\forall u,v \in \mathbf{K}^n\), \(u + v = v + u\).
3. Associativity of scalar multiplication: \(\forall u \in \mathbf{K}^n\), \(\forall \lambda, \mu \in \mathbf{K}\), \(\lambda \cdot (\mu \cdot u) = (\lambda \cdot \mu) \cdot u\).
4. Distributivity of scalar multiplication over vector addition: \(\forall \lambda \in \mathbf{K},\ u,v \in \mathbf{K}^n\), \(\lambda \cdot (u + v) = \lambda \cdot u + \lambda \cdot v\).

Proof. This follows from the properties of associativity, distributivity, and commutativity in \(\mathbf{K}\) when considering each coordinate individually.

1.3 Vector Subspaces

Let \(\mathbf{K}\) be a field and \(n\) be a positive integer.

Definition 1.6 A vector subspace of \(\mathbf{K}^n\) is a non-empty subset \(E\) of \(\mathbf{K}^n\) that satisfies the following two properties:

1. (Closed under addition) For all \(u,v \in E\), \(u + v \in E\).
2. (Closed under scalar multiplication) For all \(v \in E\) and \(\lambda \in \mathbf{K}\), \(\lambda \cdot v \in E\).

Example 1.7 In \(\mathbf{R}^2\), the line given by the equation \(x - y = 0\) is a vector subspace.

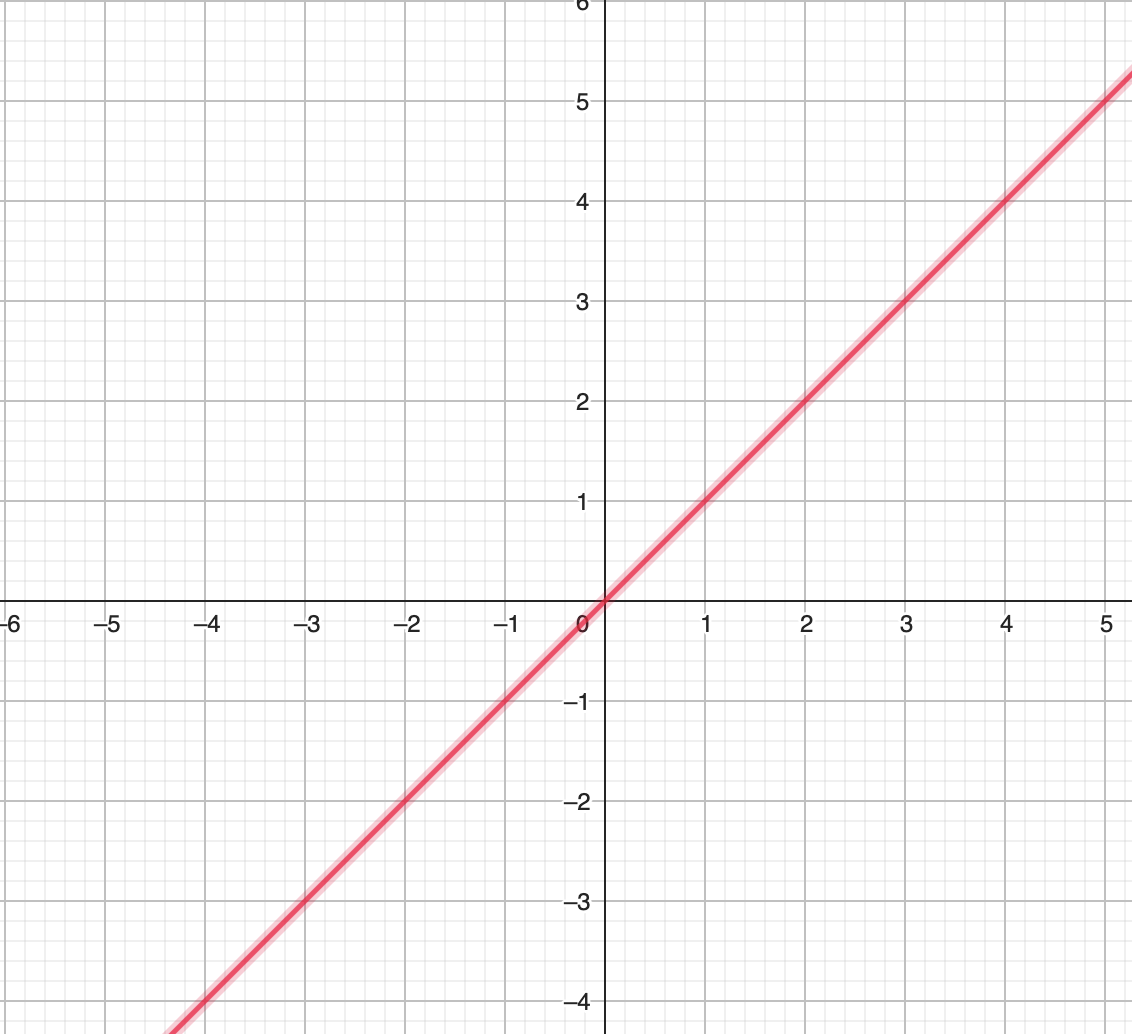
Figure 1.1: Line x-y=0

Example 1.8 In \(\mathbf{R}^3\), the plane given by the equation \(x + y + z = 0\) is a vector subspace.

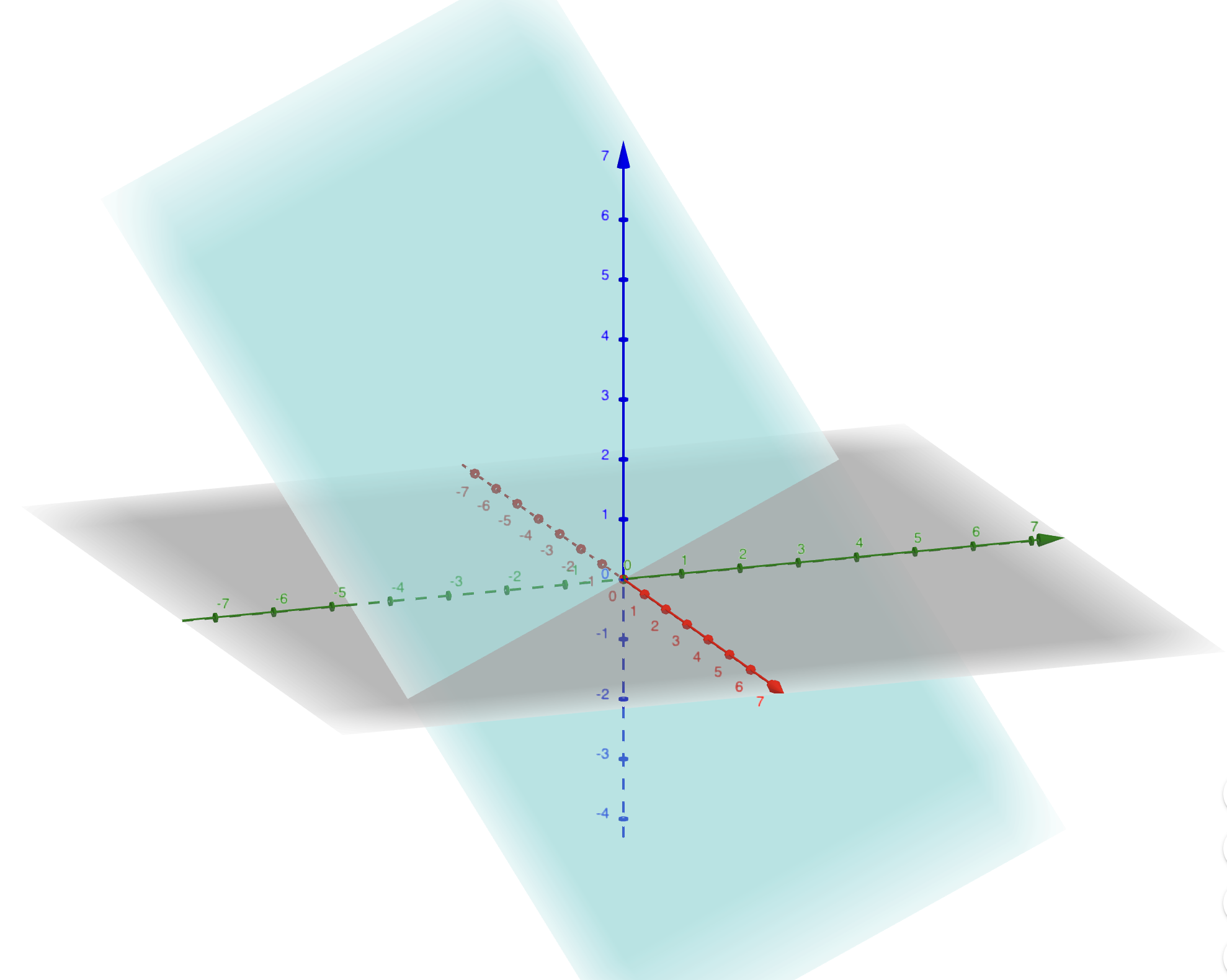
Figure 1.2: Plane x+y+z=0

Remark. A vector subspace \(E\) always contains the zero vector \(0\). Indeed, since \(E \neq \emptyset\), there exists \(v \in E\) and \(0 = v + (-1)v \in E\).

In practice, to show that a subset is a vector subspace, it is sufficient to show that it contains the zero vector to verify that the set is not empty.

Proposition 1.2 The intersection of two vector subspaces is a vector subspace.

Proof. Let \(E_1\) and \(E_2\) be two vector subspaces. Their intersection \(E_1 \cap E_2\) satisfies:

1. Closed under addition: If \(u,v \in E_1 \cap E_2\), then \(u,v \in E_1\) and \(u,v \in E_2\). Thus, \(u + v \in E_1\) and \(u + v \in E_2\), so \(u + v \in E_1 \cap E_2\).
2. Closed under scalar multiplication: If \(v \in E_1 \cap E_2\) and \(\lambda \in \mathbf{K}\), then \(v \in E_1\) and \(v \in E_2\). Thus, \(\lambda \cdot v \in E_1\) and \(\lambda \cdot v \in E_2\), so \(\lambda \cdot v \in E_1 \cap E_2\).

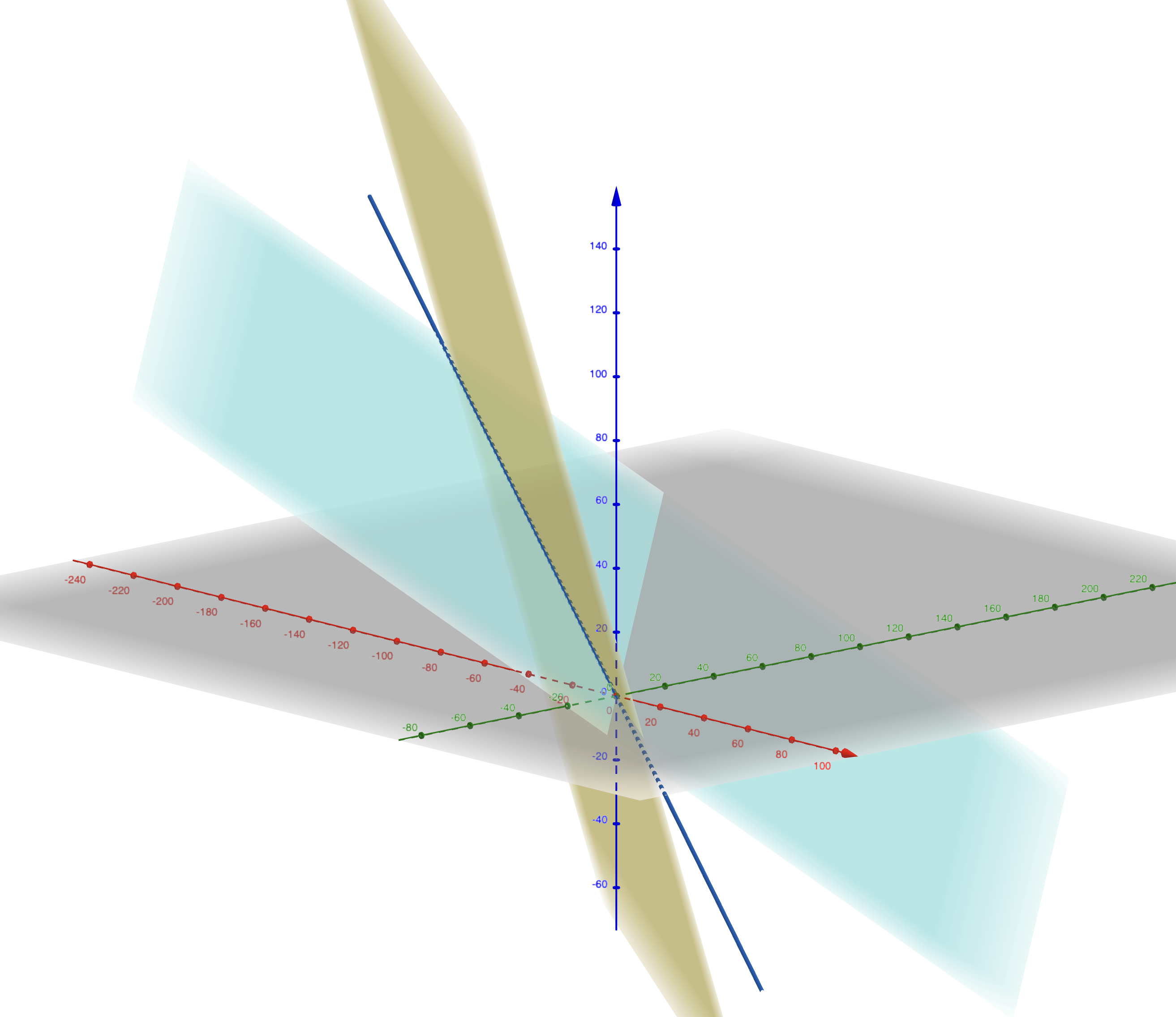
Figure 1.3: Intersection de deux plans qui est une droite

1.4 Basis

Definition 1.7 Let \(F\) be a subset of the vector space \(\mathbf{K}^n\). A vector \(v \in \mathbf{K}^n\) is a linear combination of elements of \(F\) if there exist \(v_1, \dots, v_k \in F\) and \(\lambda_1, \dots, \lambda_k \in \mathbf{K}\) such that

\[ v = \lambda_1 v_1 + \dots + \lambda_k v_k. \]

The numbers \(\lambda_1, \dots, \lambda_k\) are called the coefficients of the linear combination.

Example 1.9 The vector \(u = \begin{bmatrix} 3 \\ 6 \end{bmatrix}\) is a linear combination of the vectors \(e_1 = \begin{bmatrix} 1 \\ 4 \end{bmatrix}\) and \(e_2 = \begin{bmatrix} 1 \\ 1 \end{bmatrix}\) because

\[ u = 1 \times e_1 + 2 \times e_2. \]

Lemma 1.1 Let \(F\) be a subset of the vector space \(\mathbf{K}^n\). The set of linear combinations of elements of \(F\) forms a vector subspace of \(\mathbf{K}^n\).

Proof. Let \(E\) be the set of linear combinations of elements of \(F\). The zero vector can be written as \(0 \cdot v\) for \(v \in F\), so \(0 \in E\) and \(E \neq \emptyset\).

Let \(v \in E\) and \(\lambda \in \mathbf{K}\). Then there exist \(v_1, \dots, v_k \in F\) and \(\lambda_1, \dots, \lambda_k \in \mathbf{K}\) such that \(v = \lambda_1 v_1 + \dots + \lambda_k v_k\). We have

\[\begin{align} \lambda v &= \lambda (\lambda_1 v_1 + \dots + \lambda_k v_k) \\ &= (\lambda \lambda_1) v_1 + \dots + (\lambda \lambda_k) v_k. \end{align}\]

Thus, \(\lambda v\) is indeed a linear combination of the \(v_i\) and \(\lambda v \in E\).

Let \(u, v \in E\). Then there exist \(u_1, \dots, u_k \in F\) and \(\lambda_1, \dots, \lambda_k \in \mathbf{K}\) such that \(u = \lambda_1 u_1 + \dots + \lambda_k u_k\) and \(v_1, \dots, v_l \in F\) and \(\mu_1, \dots, \mu_l \in \mathbf{K}\) such that \(v = \mu_1 v_1 + \dots + \mu_l v_l\). Thus,

\[\begin{align} u + v &= (\lambda_1 u_1 + \dots + \lambda_k u_k) + (\mu_1 v_1 + \dots + \mu_l v_l) \\ &= \lambda_1 u_1 + \dots + \lambda_k u_k + \mu_1 v_1 + \dots + \mu_l v_l. \end{align}\]

Therefore, \(u + v\) is a linear combination of the \(u_i\) and \(v_j\) which are elements of \(F\), so \(u + v \in E\).

Definition 1.8 Let \(F\) be a subset of the vector space \(\mathbf{K}^n\). The vector subspace generated by \(F\) is the set of linear combinations of elements of \(F\).

Definition 1.9 Let \(E\) be a vector subspace of \(\mathbf{K}^n\) and \(F\) a subset of \(E\). We say that \(F\) is a generating set if \(E\) is the vector space generated by \(F\).

In other words, \(F\) is a generating set of the vector subspace \(E\) if every element of \(E\) is a linear combination of elements of \(F\). In this case, we say that \(E\) is generated by \(F\) and we write \(E = \mathrm{Vect}(F)\).

Example 1.10 Here are some examples:

1. The set \(E\) itself is a generating set for itself (any element \(v \in E\) can be written as \(v = 1 \cdot v\)).
2. The space \(\mathbf{R}^2\) is generated by the vectors \(e_1 = (1, 0)\) and \(e_2 = (0, 1)\). Indeed, any vector in \(\mathbf{R}^2\) can be written in the form \((x, y)\), which decomposes into \(x e_1 + y e_2\).
3. In \(\mathbf{R}^3\), the set \(E = \{ (x, y, z) \mid x + y + z = 0 \}\) is a vector subspace generated by the vectors \(u = (1, -1, 0)\) and \(v = (0, -1, 1)\). Indeed, if \((x, y, z) \in E\), then \((x, y, z) = x \cdot u + z \cdot v = (x, -x - z, z) = (x, y, z)\) because \(y = -x - z\) (since \(x + y + z = 0\)).

Remark. For a given vector subspace, there is no unique generating set. For example, the space \(\mathbf{R}^2\) is generated by the set \(\{ (1, 0), (0, 1) \}\) but also by the set \(\{ (1, 1), (1, -1) \}\):

\[\begin{align} (x, y) &= \frac{x}{2} \left[(1, 1) + (1, -1) \right] + \frac{y}{2} \left[(1, 1) - (1, -1) \right] \\ &= \left( \frac{x}{2} + \frac{y}{2} \right) (1, 1) + \left( \frac{x}{2} - \frac{y}{2} \right) (1, -1). \end{align}\]

Definition 1.10 A set \(F\) in \(\mathbf{K}^n\) is said to be linearly independent if no element of \(F\) can be expressed as a linear combination of the other elements of \(F\).

A set that is not linearly independent is called a linearly dependent set.

Definition 1.11 A linear combination \(\lambda_1 u_1 + \dots + \lambda_k u_k\) is said to be trivial if \(\lambda_1 = \dots = \lambda_k = 0\), and it is said to be null if \(\lambda_1 u_1 + \dots + \lambda_k u_k = 0\).

Remark. A trivial linear combination is always null, but the converse is not always true. Exercise: find a counterexample!

Lemma 1.2 A set \(F\) is linearly independent if and only if every null linear combination of elements of \(F\) is trivial:

\[ \forall u_1, \dots, u_k \in F, \ \lambda_1, \dots, \lambda_k \in \mathbf{K}; \ \lambda_1 u_1 + \dots + \lambda_k u_k = 0 \implies \lambda_1 = \dots = \lambda_k = 0. \]

Proof. By contraposition, the statement is equivalent to “A set \(F\) is linearly dependent if and only if there exists a non-trivial null linear combination of elements of \(F\).”

Let \(u_1, \dots, u_k \in F\). If \(u_i\) is a linear combination of the other \(u_j\), then there exist \(\lambda_1, \dots, \lambda_{i-1}, \lambda_{i+1}, \dots, \lambda_k \in \mathbf{K}\) such that

\[ u_i = \lambda_1 u_1 + \dots + \lambda_{i-1} u_{i-1} + \lambda_{i+1} u_{i+1} + \dots + \lambda_k u_k, \] and thus

\[ \lambda_1 u_1 + \dots + \lambda_{i-1} u_{i-1} - u_i + \lambda_{i+1} u_{i+1} + \dots + \lambda_k u_k = 0. \]

This gives a non-trivial null linear combination (the coefficient of \(u_i\) is non-zero).

Conversely, let \(u_1, \dots, u_k \in F\) and \(\lambda_1 u_1 + \dots + \lambda_k u_k = 0\) be a null linear combination. Suppose for contradiction that there exists \(\lambda_i \neq 0\). Then

\[ u_i = \frac{1}{\lambda_i} \left( \sum_{j \neq i} \lambda_j u_j \right), \]

so \(u_i\) is a linear combination of the other \(u_j\). This contradicts the linear independence. Thus, all the \(\lambda_i\) must be zero, and the linear combination is trivial.

Example 1.11 Some examples.

1. The set \(\{(1,0),(0,1),(1,1)\}\) is linearly dependent because \((1,1) = (1,0) + (0,1)\).
2. The set \(\{(1,1),(1,-1)\}\) is linearly independent. Indeed, if \(\lambda(1,1) + \mu(1,-1) = (0,0)\), then solving the system

\[\left\{\begin{matrix} \lambda + \mu &= 0 \\ \lambda - \mu &= 0 \end{matrix} \right.\]

we find \(\lambda = 0\) and \(\mu = 0\). This shows that the set is linearly independent.

Definition 1.12 Let \(E\) be a subspace of \(\mathbf{K}^n\). A basis of \(E\) is a linearly independent and generating set for \(E\).

Example 1.12 The set \((e_1, \dots, e_n)\) where \(e_i = (0, \dots, 0, 1, 0, \dots, 0)\) with a 1 in the \(i\)-th position is a basis of \(\mathbf{K}^n\) called the canonical basis. The coordinates \(v_i\) of a vector \(v = (v_1, \dots, v_n)\) are exactly the coordinates of \(v\) in the canonical basis since

\[v = \sum_{i=1}^n v_i e_i.\]

Lemma 1.3 Let \(E\) be a subspace of \(\mathbf{K}^n\). A set \(\mathcal{B} = (u_1, \dots, u_k)\), where each \(u_i \in E\), is a basis of \(E\) if and only if for every vector \(u \in E\), there exists a unique \(k\)-tuple \((\lambda_1, \dots, \lambda_k) \in \mathbf{K}^k\) such that

\[u = \lambda_1 u_1 + \dots + \lambda_k u_k.\]

The numbers \(\lambda_1, \dots, \lambda_k \in \mathbf{K}\) are called the coordinates of \(u\) in the basis \(\mathcal{B}\). Note that a basis is not just a subset but an ordered sequence of vectors.

Proof. The existence of \((\lambda_1, \dots, \lambda_k) \in \mathbf{K}^k\) is equivalent to the set being generating.

If there are two \(k\)-tuples \((\lambda_1, \dots, \lambda_k) \in \mathbf{K}^k\) and \((\mu_1, \dots, \mu_k) \in \mathbf{K}^k\) such that

\[u = \lambda_1 u_1 + \dots + \lambda_k u_k\]

and

\[u = \mu_1 u_1 + \dots + \mu_k u_k\] then \[(\lambda_1 - \mu_1) u_1 + \dots + (\lambda_k - \mu_k) u_k = 0.\]

This results in a trivial linear combination if and only if \(\lambda_i = \mu_i\) for all \(i\). Thus, the uniqueness of the linear combination of the \(u_i\) is equivalent to the linear independence of \((u_1, \dots, u_k)\).

Proposition 1.3 Let \(E\) be a subspace of \(\mathbf{K}^n\). If \(\{u_1, \cdots, u_k\}\) is a generating set for \(E\), then any set of \(E\) with strictly more than \(k\) elements is linearly dependent.

Proof. We prove the result by induction on \(k\).

If \(k = 0\), then \(E = \{0\}\). The only element in \(E\) is the zero vector, so any linear combination is zero.

Assume the result for \(k-1 \geq 0\). Let \(E\) be a subspace spanned by \(k\) vectors \(u_1, \dots, u_k\), and let \(F = \{f_1, \dots, f_{k+1}\}\) be a set of \(k+1\) vectors (which demonstrates the result for any set with a greater cardinality). Since the set \(\{u_1, \dots, u_k\}\) is generating, for each \(1 \leq j \leq k+1\), there exist \(a_{1,j}, \dots, a_{k,j}\) such that

\[f_j = \sum_{i=1}^k a_{i,j} u_i.\] If all \(a_{k,j}\) for \(j = 1, \dots, k+1\) are zero, then the set is within \(\mathrm{Vect}(u_1, \dots, u_{k-1})\), and by the induction hypothesis, it is linearly dependent. Otherwise, by possibly reordering the elements of \(F\), we can assume that \(a_{k,k+1} \neq 0\). For \(1 \leq j \leq k\), let

\[\begin{align} f'_j &= f_j - \frac{a_{k,j}}{a_{k,k+1}} f_{k+1} \\ &= \sum_{i=1}^k \left(a_{i,j} - \frac{a_{k,j}}{a_{k,k+1}} a_{i,k+1}\right) u_i \\ &= \sum_{i=1}^{k-1} \left(a_{i,j} - \frac{a_{k,j}}{a_{k,k+1}} a_{i,k+1}\right) u_i \end{align}\] because the coefficient in front of \(u_k\) is zero.

The set \(\{f'_1, \dots, f'_k\}\) is in the space spanned by \(\mathrm{Vect}(u_1, \dots, u_{k-1})\). By the induction hypothesis, the set \(\{f'_1, \dots, f'_k\}\) is linearly dependent, so there exist \(\alpha_1, \dots, \alpha_k \in \mathbf{K}\), not all zero, such that

\[\sum_{j=1}^k \alpha_j f'_j = 0.\] This gives

\[\alpha_1 f_1 + \dots + \alpha_k f_k - \left(\sum_{j=1}^k \alpha_j \frac{a_{k,j}}{a_{k,k+1}}\right) f_{k+1} = 0.\] Since this linear combination is not trivial, the set \(\{f_1, \dots, f_{k+1}\}\) is linearly dependent.

By induction, the result is assured for all \(k \in \mathbf{N}\).

Corollary 1.1 Two bases of the same subspace have the same number of elements.

Proof. Let \((u_1, \dots, u_k)\) and \((v_1, \dots, v_l)\) be two bases of the same vector space. Since \(\{u_1, \dots, u_k\}\) is generating and \(\{v_1, \dots, v_l\}\) is linearly independent, Proposition 1.3 shows that \(l \leq k\). Swapping the roles of the two bases, we get \(k \leq l\), hence \(k = l\).

1.5 Dimension

The previous corollary allows us to define the dimension of a vector space based on any basis.

Definition 1.13 The dimension of a subspace is the cardinality of a basis of that subspace. We denote this number by \(\dim(E)\).

A subspace of dimension 1 is called a line and a subspace of dimension 2 is called a plane.

Example 1.13 Here are two examples:

1. The dimension of the space \(\mathbf{K}^n\) is exactly \(n\) since the canonical basis has \(n\) elements.
2. The subspace defined by the equation \(x+y+z=0\) in \(\mathbf{R}^3\) has a basis \((u_1, u_2)\) where \(u_1=(1,-1,0)\) and \(u_2=(0,-1,1)\). Thus, this space has dimension 2. Hence, it is a vector plane.

Lemma 1.4 Let \(E\) and \(E'\) be two vector subspaces of \(\mathbf{K}^n\). If \(E \subset E'\), then \(\dim(E) \leq \dim(E')\), and \(E = E'\) if and only if \(\dim(E) = \dim(E')\).

Proof. Let \(k = \dim(E')\) be the cardinality of a basis of \(E'\). Any basis of \(E\) is a linearly independent family within \(E'\) and therefore has a cardinality less than \(k\) by Proposition 1.3. Thus, \(\dim(E) \leq \dim(E')\).

Now, if \(E = E'\), we have \(\dim(E) = \dim(E')\) obviously. Conversely, if \(E \subseteq E'\) and \(E \neq E'\), then there exists \(u \in E' \setminus E\). For any basis \(e_1, \dots, e_k\), the family \(\{e_1, \dots, e_k, u\}\) is linearly independent (otherwise \(u \in \mathrm{Vect}(e_1, \dots, e_k) = E\)), so \(\dim(E') \geq \dim(E) + 1 > \dim(E)\). Thus, by contrapositive, if \(\dim(E) = \dim(E')\), then \(E = E'\).

Theorem 1.1 (Incomplete Basis Theorem) Any linearly independent family \((u_1, \dots, u_k)\) of a vector subspace \(E\) can be extended by elements of \(E\) to form a basis of \(E\): there exist \(u_{k+1}, \dots, u_l\) such that \((u_1, \dots, u_l)\) is a basis of \(E\).

Proof. Let \(E_1 = \mathrm{Vect}(u_1, \dots, u_k)\), which has dimension \(k\), and let \(n = \dim(E)\). If \(E_1 \neq E\), then there exists \(u_{k+1} \in E \setminus E_1\). The family \((u_1, \dots, u_k, u_{k+1})\) is linearly independent, so \(E_2 = \mathrm{Vect}(u_1, \dots, u_k, u_{k+1})\) has dimension \(k+1\). We repeat the process to build \(E_1, E_2, E_3, \dots, E_{n-k+1}\) by choosing a vector \(u_l \in E \setminus E_{l-k}\) at each step. Thus, the dimension of \(E_j\) increases by 1 at each step, so \(\dim(E_{n-k+1}) = n\). By Lemma 1.4, we have \(E_{n-k+1} = E\). This shows that \((u_1, \dots, u_n)\) is a basis of \(E\).

Theorem 1.2 Let \(E\) be a vector subspace. From any generating family \(F\), one can extract a basis: there exist \(u_1, \dots, u_k \in F\) such that \((u_1, \dots, u_k)\) is a basis of \(E\).

Proof. The vector subspace \(E\) is a subspace of some \(\mathbf{K}^n\). Any linearly independent family in \(F\) has at most \(n\) elements by Proposition 1.3. We choose a linearly independent family \(\{e_1, \dots, e_k\}\) with maximal cardinality in \(F\). This family is generating. Indeed, if there existed \(u \in E\) not in \(\mathrm{Vect}(e_1, \dots, e_k)\), then \(\{e_1, \dots, e_k, u\}\) would be linearly independent, contradicting the maximality of \(\{e_1, \dots, e_k\}\). Thus, there exist \(\alpha_1, \dots, \alpha_{k+1} \in \mathbf{K}\) such that

\[\alpha_1 e_1 + \dots + \alpha_k e_k + \alpha_{k+1} u = 0.\]

Since \(\{e_1, \dots, e_k\}\) is linearly independent, necessarily \(\alpha_{k+1} \neq 0\). Thus, \(u = -\frac{1}{\alpha_{k+1}}(\alpha_1 e_1 + \dots + \alpha_k e_k) \in \mathrm{Vect}(e_1, \dots, e_k)\). This shows that \(\{e_1, \dots, e_k\}\) is generating and hence is a basis.

Corollary 1.2 Every vector subspace has at least one basis. In particular, every vector subspace has a well-defined dimension.

Proof. This corollary can be proved using either of the two theorems above. We use Theorem 1.2. Let \(E\) be a vector subspace. Since the entire set \(E\) is a generating family of itself, one can extract a basis of \(E\) from it.

1.6 Exercises

Exercise 1.1 Verify that \(\mathbf{F}_2\) with the given addition and multiplication tables is indeed a field.

Exercise 1.2 In \(\mathbf{F}_2\), identify \(0\) with the boolean value FALSE and \(1\) with the boolean value TRUE. Show that \(xy\) corresponds to the boolean operation “\(x\) and \(y\)” while \(x + y + xy\) corresponds to the operation “\(x\) or \(y\)”. What boolean operation corresponds to the addition \(x + y\)?

Exercise 1.3 Is the union of two vector subspaces \(E_1\) and \(E_2\) a vector subspace? You might consider the example given by \(E_1 = \{(x, y) \in \mathbf{R}^2 \mid x + y = 0\}\) and \(E_2 = \{(x, y) \in \mathbf{R}^2 \mid x - y = 0\}\) by plotting them.

Exercise 1.4 Are the following families linearly independent and generating sets of \(\mathbf{R}^n\)? Are they bases of \(\mathbf{R}^n\)?

1. \(\begin{bmatrix}1\\2\end{bmatrix}\) and \(\begin{bmatrix}1\\3\end{bmatrix}\) in \(\mathbf{R}^2\).
2. \(\begin{bmatrix}1\\2\end{bmatrix}\) and \(\begin{bmatrix}3\\6\end{bmatrix}\) in \(\mathbf{R}^2\).
3. \(\begin{bmatrix}1\\2\end{bmatrix}\), \(\begin{bmatrix}3\\5\end{bmatrix}\), and \(\begin{bmatrix}4\\2\end{bmatrix}\) in \(\mathbf{R}^2\).
4. \(\begin{bmatrix}1\\2\\3\end{bmatrix}\) and \(\begin{bmatrix}4\\5\\6\end{bmatrix}\) in \(\mathbf{R}^3\).
5. \(\begin{bmatrix}1\\2\\3\end{bmatrix}\), \(\begin{bmatrix}5\\7\\9\end{bmatrix}\), and \(\begin{bmatrix}4\\5\\6\end{bmatrix}\) in \(\mathbf{R}^3\).
6. \(\begin{bmatrix}1\\2\\3\end{bmatrix}\), \(\begin{bmatrix}5\\7\\9\end{bmatrix}\), and \(\begin{bmatrix}7\\11\\13\end{bmatrix}\) in \(\mathbf{R}^3\).

Exercise 1.5 Consider the vectors \(e_1 = \begin{bmatrix}1\\1\\1\end{bmatrix}\) and \(e_2 = \begin{bmatrix}1\\-1\\1\end{bmatrix}\).

1. Show that they form a linearly independent set in \(\mathbf{R}^3\).
2. Represent the vector subspace spanned by these vectors.
3. Extend this family to a basis \((e_1, e_2, e_3)\) of \(\mathbf{R}^3\).

Exercise 1.6 Consider \(u_1 = \begin{bmatrix}1\\2\\3\end{bmatrix}\), \(u_2 = \begin{bmatrix}5\\7\\9\end{bmatrix}\), and \(u_3 = \begin{bmatrix}4\\5\\6\end{bmatrix}\) in \(\mathbf{R}^3\). Let \(V\) be the vector subspace spanned by these vectors.

1. Extract a basis of \(V\) from the family \((u_1, u_2, u_3)\).
2. What is the dimension of \(V\)?
3. Find a linear equation for \(V\), i.e., find coefficients \(a, b, c \in \mathbf{R}\) such that \[\begin{bmatrix}x\\y\\z\end{bmatrix} \in V \iff ax + by + cz = 0.\]

Exercise 1.7 Consider the vectors \(\begin{bmatrix}1\\1\end{bmatrix}\) and \(\begin{bmatrix}1\\0\end{bmatrix}\).

1. Show that these vectors form a basis of \(\mathbf{F}_2^2\).
2. What are the coordinates of the vector \(\begin{bmatrix}0\\1\end{bmatrix}\) in this basis?

Exercise 1.8 Let \(\mathbf{K}\) be a field.

1. Show that any linearly independent family in \(\mathbf{K}^n\) has at most \(n\) elements.
2. Show that any generating family of \(\mathbf{K}^n\) has at least \(n\) elements.
3. Show that any linearly independent family in \(\mathbf{K}^n\) is a basis if and only if it has exactly \(n\) elements.
4. Show that any generating family of \(\mathbf{K}^n\) is a basis if and only if it has exactly \(n\) elements.

Exercise 1.9 Consider the field \(\mathbf{K} = \mathbf{F}_2\). What is the cardinality of a vector subspace of dimension \(n\)?

Exercise 1.10 Show that the following sets are vector subspaces of \(\mathbf{R}^3\).

1. \(E_2 = \{(x, y, z) \in \mathbb{R}^3 \mid 3x - 7y = z\}\). Determine a basis and its dimension.
2. \(E_3 = \{(x, y, z) \in \mathbb{R}^3 \mid x + y - z = 0 \text{ and } x + y + z = 0\}\). Determine a basis and its dimension.

Exercise 1.11 Consider two planes in \(\mathbf{R}^3\): \[P_1 = \{(x, y, z) \in \mathbf{R}^3 \mid x - y + z = 0\}\] \[P_2 = \{(x, y, z) \in \mathbf{R}^3 \mid x - y = 0\}\] Find a basis for \(P_1 \cap P_2\). What is its dimension?

Exercise 1.12 Let \(n \in \mathbf{N}\). Denote by \(\mathcal{P}_n\) the set of polynomials of degree at most \(n\). Identify the polynomial \(a_n X^n + \dots + a_1 X + a_0\) with the vector \((a_0, \dots, a_n) \in \mathbf{R}^{n+1}\).

1. If \(P = a_n X^n + \dots + a_1 X + a_0\) and \(Q = b_n X^n + \dots + b_1 X + b_0\), to which vector corresponds the polynomial \(P + Q\)?
2. Same question for the polynomial \(\lambda P\) where \(\lambda \in \mathbf{R}\).
3. To which family of polynomials does the canonical basis of \(\mathbf{R}^{n+1}\) correspond?
4. Show that the set \(E_1 = \{P \in \mathcal{P}_n \mid P(1) = 0\}\) is a vector subspace of \(\mathcal{P}_n\).
5. For each \(k \leq n\), find a polynomial \(P_k\) of degree \(k\) such that \(P_k \in E_1\).
6. Provide a basis for \(E_1\) and deduce its dimension.