Chapitre 4 Problèmes de décision pour les automates

4.1 Décidabilité

La question de la décidabilité (décidabilité algorithmique plus précisément) est une question importante en informatique théorique. D’une manière un peu vague, une question est décidable s’il existe un algorithme qui s’arrête en temps fini qui répond à la question.

De manière équivalente, une question ou un problème est décidable si on peut (au moins théoriquement) répondre à la question à l’aide d’un ordinateur. En pratique, on peut cependant être limité par des questions de temps d’éxécution ou de capacité mémoire.

Pour illustrer cette question de décidabilité, voyons deux exemples. Par exemple, le problème de trouver le plus chemin entre deux sommets dans un graphe fini est décidable car il existe un algorithme qui répond à cette question, c’est l’algorithme de Dijkstra. On peut aussi penser au problème le pgcd de deux nombres entiers. Une réponse est donnée par l’algorithme d’Euclide.

Une question classique d’informatique est de savoir si un algorihtme va se terminer. Étant donné un algorithme peut-on décider simplement en examinant le code si le programme va se terminer ou pas ? Autrement dit, peut-on écrire un algorithme qui prend en entrée un algorithme et retourne oui ou non selon que le programme s’arrête ou non. Par exemple, s’il y a une boucle “tant que”, on n’est pas sûr que la condition soit remplie et que le programme s’arrête. C’est le problème de l’arrêt.

Alan turing (un des fondateurs de l’informatique théorique) a démontré en 1936 que ce problème n’avait pas de réponse positive. Il y a donc des problèmes indécidables et cela limite donc les possibilités d’un ordinateur. Pour démontrer cette indécidabilité, il inventa une machine théorique, la fameuse machine de Turing, qui formalise ce que veut dire faire un calcul (ou autrement dit exécuter un algorithme).

Figure 4.1: Alan Turing.

Il s’agit d’une machine composée d’une ruban infinie avec des cases contenant des 0 et des 1 (ce qui correspond à la mémoire de la machine), d’une tête de lecture pouvant lire ou écrire une case et se déplacer vers la droite ou la gauche d’une case. Une liste d’instructions (le programme informatique) explique ce que doit faire la tête de lecture selon la case où elle se trouve et ce qu’elle y lit.

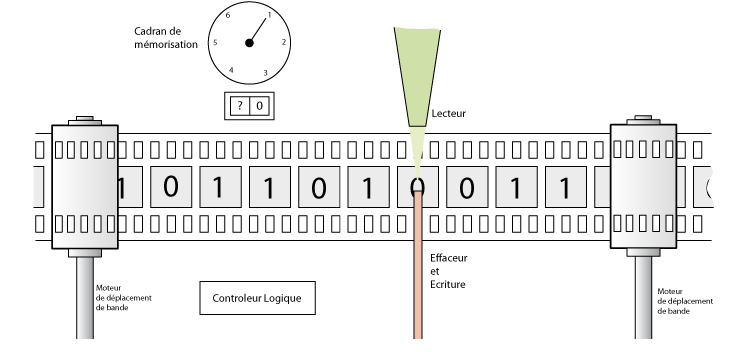
Figure 4.2: Une machine de Turing.

Figure 4.3: Une machine de Turing en légo réalisée à l’ENS de Lyon.

Dans la suite de ce chapitre, on s’intéresse à quelques questions de décidabilité pour les automates

4.2 Vacuité du langage reconnu

La vacuité est le fait d’être vide. Étant donné un automate \(A\), existe-t-il un mot reconnu par \(A\) ? Autrement dit, a-t-on \(\mathcal{L}(A)\neq\emptyset\) ? C’est le problème du langage vide.

Proposition 4.1 Le problème de la vacuité du langage reconnu par un automate est décidable.

Preuve. Il existe au moins un mot reconnu par l’automate (éventuellement le mot vide), s’il existe une exécution de l’automate qui aboutit à un état final. Ce qui signifie exactement qu’il existe un chemin de l’état initial à un état final.

Pour vérifier qu’il existe un tel chemin, il suffit de faire un parcours (en profondeur ou en largeur) pour vérifier qu’un état final est accessible depuis l’état initial. Nous avons un algorithme qui répond à cette question en cours de théorie des graphes.

4.3 Infinitude du langage reconnu

On peut aussi se demander si le langage reconnu est infini. C’est le problème de l’infinitude du langage reconnu.

Proposition 4.2 Le problème de l’infinitude du langage reconnu par un automate est décidable.

Preuve. Dans le graphe associé à l’automate, le nombre de chemins simples (ceux qui ne repassent pas deux fois par le même sommet) sont en nombre fini (au plus \((n-1)!\) si \(n\) est le nombre d’états). Il y a une infinité de mots reconnus si et seulement s’il existe un chemin de l’état initial qui contient un circuit. Un mot reconnu par l’automate correspondant à ce chemin est alors de la forme

\[m_1\cdot m_2\cdot m_3\] où \(m_2\) correspond à la partie lue par le circuit.

Ainsi, tous les mots de la forme \(m_1\cdot m_2^n\cdot m_3\) (pour \(n\in\mathbb{N}\)) seront reconnus par l’automate. Cela correspond à faire \(n\) le fois circuit.

Le problème se reformule ainsi de la manière équivalente suivante : existe-t-il un chemin du sommet initial à un sommet final qui contient une boucle ? On peut utiliser un algorithme de parcours de graphe et l’adapter pour détecter un tel chemin donc le problème de l’infinitude est décidable.

4.4 Équivalence de deux automates

Une question plus intéressante est la suivante : étant donnés deux automates déterministes, les langages reconnus sont-ils les mêmes ? Autrement dit, peut-on décider si deux automates sont équivalents ? En effet, il n’est pas difficile de créer deux automates différents qui reconnaissent le même langage mais savoir si deux automates différents reconnaissent le même langage n’est pas évident et on vroudrait avoir un algorithme pour pouvoir répondre à cette question.

Exemple 4.1

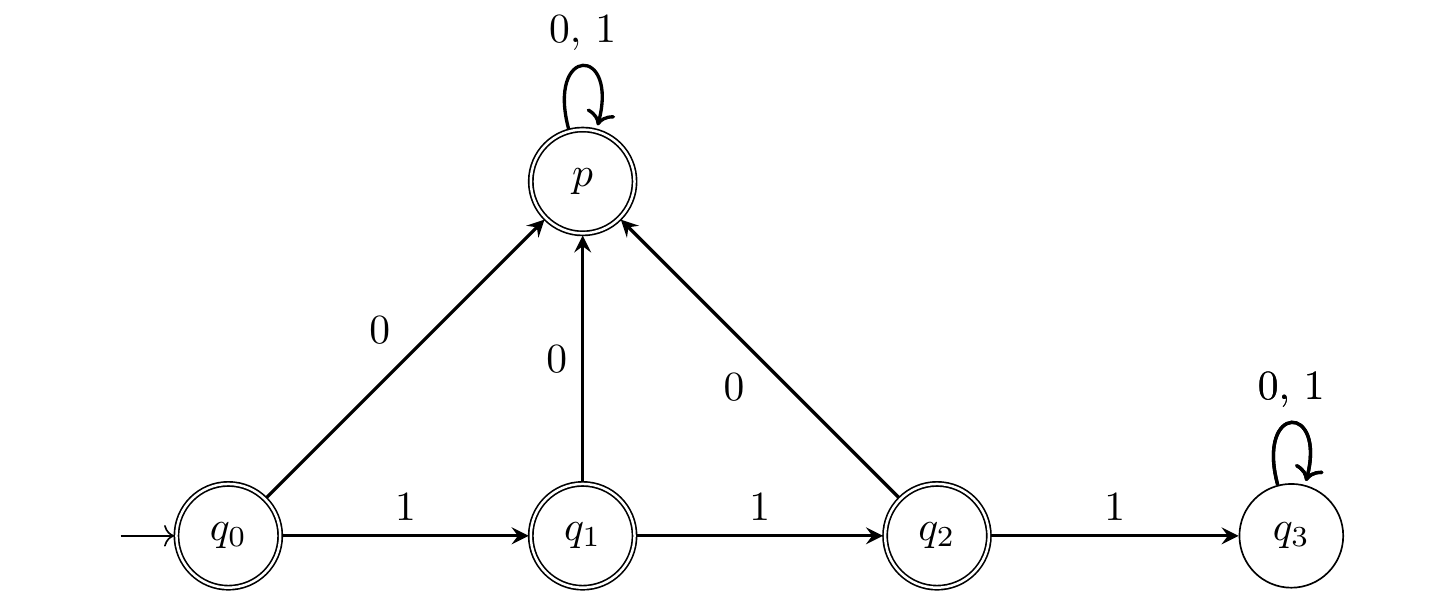
Figure 4.4: Un automate déterministe non complet qui reconnait les mots de longueur au moins deux.

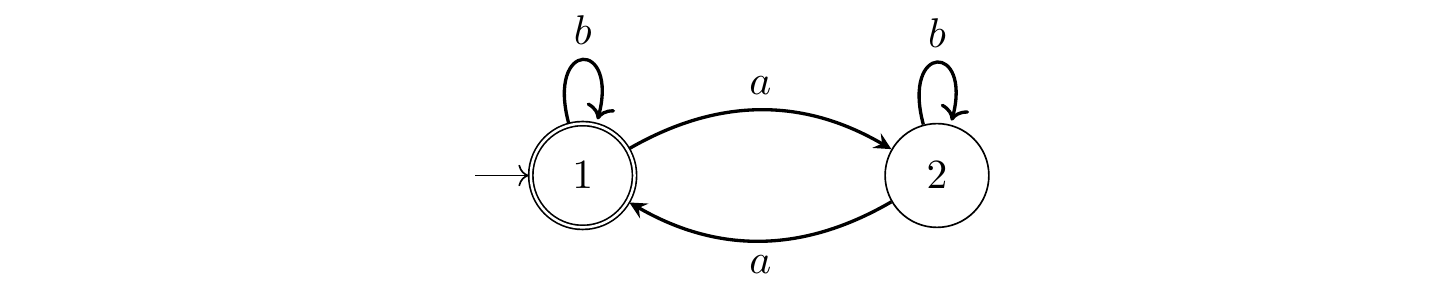
Figure 4.5: Un autre automate déterministe non complet qui reconnait le même langage.

Lemme 4.1 Soit \(L,L'\) deux langages sur un alphabet \(\mathcal{A}\). On a l’inclusion \(L\subset L'\) si et seulement si \(L^c\cap L'=\emptyset\).

Étant donné deux automates \(A,A'\), le problème de l’inclusion des langages est celui de trouver un algorithme qui permette de savoir si \(\mathcal{L}(A)\subseteq\mathcal{L}(A')\).

Proposition 4.3 Le problème de l’inclusion des langages est décidable

Preuve. Grâce au Lemma 4.1, il suffit de décider si \(\mathcal{L}(A)^c\cap\mathcal{L}(A')=\emptyset\). Nous avons un algorithme pour construire l’automate \(A''\) à partir de \(A\) qui reconnait le langage complémentaire \(\mathcal{L}(A)^c\) et nous avons un algorithme qui construit un automate qui reconnait l’intersection des langages \(\mathcal{L}(A)^c\) et \(\mathcal{L}(A')\) (c’est l’automate produit \(A''\times A'\)) donc en combinant ces deux algorithmes, nous avons un algorithme qui décide si deux automates ont un langage inclus l’un dans l’autre.

Théorème 4.1 L’équivalence de deux automates finis déterministes est un problème décidable.

Preuve. Il s’agit de montrer qu’il existe un algorithme qui prend en entrée deux automates finis \(A,A'\) et retourne vrai ou faux selon que \(\mathcal{L}(A)=\mathcal{L}(A')\). Cette égalité est équivalente à la double inclusion \(\mathcal{L}(A)\subseteq\mathcal{L}(A')\) et \(\mathcal{L}(A')\subseteq\mathcal{L}(A)\). Par la Proposition 4.3, nous avons un algorithme qui répond à chacune de ces deux questions. En les combinant, on obtient donc un algorithme qui répond à la question de l’équivalence des langages reconnu par deux automates.

4.5 Minimisation d’automates

Dans la section précédente, nous avons vu que des automates différents \(A\) et \(A'\) peuvent reconnaître le même langage (Exemple 4.1). Pour un langage reconnaissable donné \(L\), on peut se demander s’il existe un automate \(A\) le plus simple possible tel que \(\mathcal{L}(A)=L\). Ici, on va quantifier la simplicité d’un automate par son nombre d’états.

Définition 4.1 Un automate déterministe complet \(A\) est minimal si pour tout autre automate déterministe \(A'\) reconnaissant le même langage, \(|Q|\leq |Q'|\) où \(Q\) et \(Q'\) sont respectivement les ensembles d’états de \(A\) et \(A'\).

Remarque. Pour un langage donné, il n’existe pas nécessairement un unique automate minimal qui le reconnaît. Par définition, si deux automates minimaux reconnaissent le même langage alors ils ont même nombre d’états.

Nous allons voir comment trouver algorithmiquement à partir d’un automate \(A\), un automate \(A'\) minimal tel que \(\mathcal{L}(A')=\mathcal{L}(A)\). C’est le processus de minimisation.

Définition 4.2 Soit \(A=(Q,i,\mathcal{A},\delta,F)\) un automate déterministe. Deux états \(q,q'\in Q\) sont équivalents si les mots acceptés à partir de \(q\) ou \(q'\) sont les mêmes. C’est-à-dire pour tout mot \(m\in\mathcal{A}^*\),

\[\delta^*(q,m)\in F\iff \delta^*(q',m)\in F.\]

On notera \(q\sim q'\) pour dire que \(q\) et \(q'\) sont équivalents. Nous allons vouloir vérifier algorithmiquement que deux états sont équivalents. Pour cela nous allons procéder de manière itérative.

Soit \(A\) un automate déterministe complet, \(q,q'\) deux états et \(k\in\mathbb{N}\). On dit que \(q\) et \(q'\) sont équivalents en \(k\)-étapes si pour tout mot \(m\) de longueur inférieur à \(k\),

\[\delta^*(q,m)\in F\iff \delta^*(q',m)\in F.\]

On notera alors \(q\sim_k q'\) pour cette relation d’équivalence. Par définition, on a \(q\sim q'\) si et seulement si \(q\sim_k q'\) pour tout \(k\in \mathbb{N}\).

Remarque. On a \(q\sim_0 q'\) si seulement si \(q\in F\wedge q'\in F\) ou \(q\notin F\wedge q'\notin F\).

Lemme 4.2 Pour deux états \(q,q'\) d’un automate déterministe complet et \(k\geq 1\),

\[q\sim_k q'\iff \forall a\in\mathcal{A},\ \delta(q,a)\sim_{k-1}\delta(q',a).\]

Preuve. En effet, tout mot \(m\) longueur \(k\) s’écrit \(m=am'\) avec \(a\in\mathcal{A}\) et \(|m'|=k-1\). Alors \(\delta^*(q,m)\in F\iff \delta^*(\delta(a,q),m')\in F\) et de même \(\delta^*(q,m)\in F\iff \delta^*(\delta(a,q),m')\in F\). Ce qui donne l’équivalence désirée.

Proposition 4.4 Il existe un algorithme qui calcule les classes d’équivalence des états d’un automate.

Preuve. On écrit un algorithme de la manière suivante.

On crée \(R_0\) qui contient tous les couples équivalents en \(0\) étapes. Itérativement, on crée \(R_{k+1}\) à partir de \(R_{k}\) de la manière suivante. On pose

\[D_k=\{(p,q)\in R_{k},\ \exists a\in\mathcal{A},\ (\delta(p,a),\delta(q,a))\notin R_{k}\}.\] Puis \(R_{k+1}=R_k\setminus D_k\).

On s’arrête lorsque \(R_{k+1}=R_k\). A ce moment-là \(R_k\) contient tous les couples \((p,q)\) avec \(p\sim q\).

Théorème 4.2 Soit \(A\) un automate fini déterministe complet. Il existe un algorithme qui calcule un automate minimal reconnaissant le même langage que \(A\).

Preuve. On commence par calculer l’ensemble \(Q_\sim\) des classes d’états équivalents avec l’algorithme précédent. Ensuite on définit l’automate quotient \(A_\sim=(Q_\sim,[i],\mathcal{A},\delta_\sim, F_\sim)\) où

• \([i]\) est la classe de l’état initial,
• \(\delta_\sim([q],a)=[\delta(q,a)]\),
• \(F_\sim\) est l’ensemble des classes des états terminaux

L’automate obtenu est appelé automate minimisé.

4.6 Exercices

Exercice 4.1 Écrire en pseudo-code un algorithme qui prend en entrée un automate fini déterministe \(A\) et retourne vrai ou faux selon que \(\mathcal{L}(A)\) est infini ou fini.

Exercice 4.2 Démontrer que la relation “être équivalent” sur les états d’un automate est bien une relation d’équivalence.

Exercice 4.3 Minimiser les automates suivants.

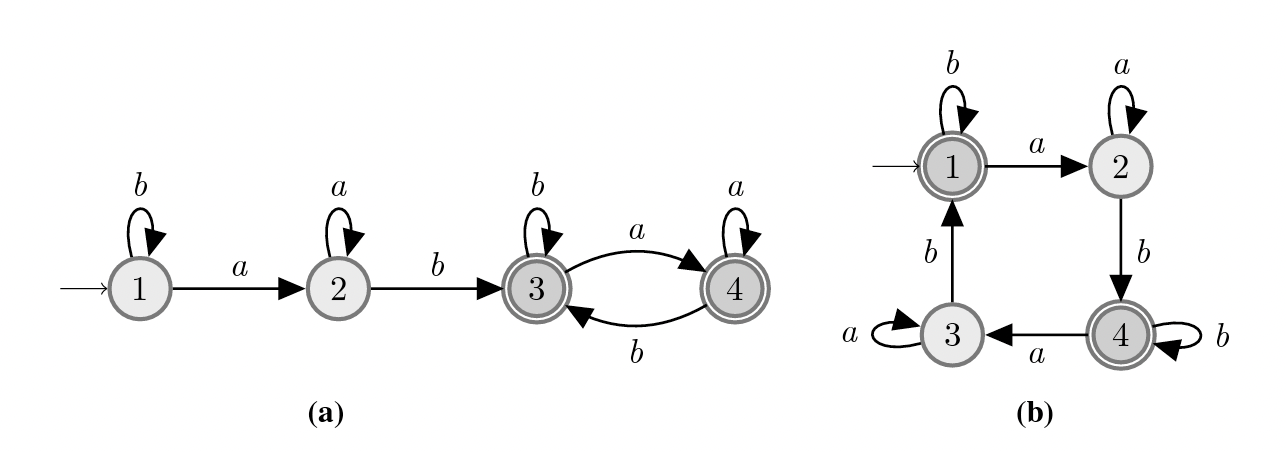
Figure 4.6: Automates à minimiser.

Exercice 4.4 Dire si les automates suivants sont équivalents.

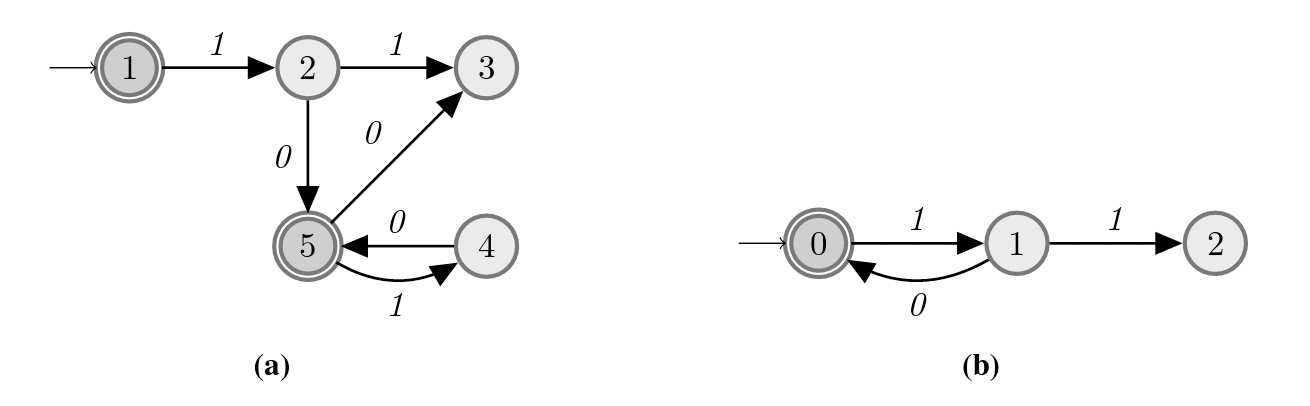
Figure 4.7: Automates équivalents ?