Chapitre 6 Automates généraux
Jusqu’ici, nous n’avons traité que d’automates déterministes. Ce sont les plus faciles à traiter théoriquement. Il existe cependant des problèmes pour lesquels, on a plus facilité à répondre au problème en introduisant des automates plus généraux que les automates déterministes commes les automates non-déterministes et les automates avec \(\varepsilon\)-transitions. Nous verrons que ces nouveaux types d’automates reconnaissent les mêmes langages que les automates déterministes
6.1 Automates non-déterministes
Définition 6.1 Un automate non déterministe est un quintuplé \((Q,\mathcal{A},i,\Delta,F)\) où
- \(Q\) est un ensemble fini d’états,
- \(\mathcal{A}\) est un alphabet,
- \(i\in Q\) est l’état initial,
- \(\Delta\subset Q\times \mathcal{A}\times Q\) est la relation de transition et
- \(F\subset Q\) est l’ensemble des états finaux
Remarque. Un automate déterministe \((Q,\mathcal{A},i,\delta,F)\) est aussi non-déterministe. Il suffit pour cela de définir \(\Delta\) de la manière suivante : \((q_1,a,q_2)\in\Delta\iff \delta(q_1,a)=q_2\). C’est le fait qu’une fonction est un cas particulier de relation.
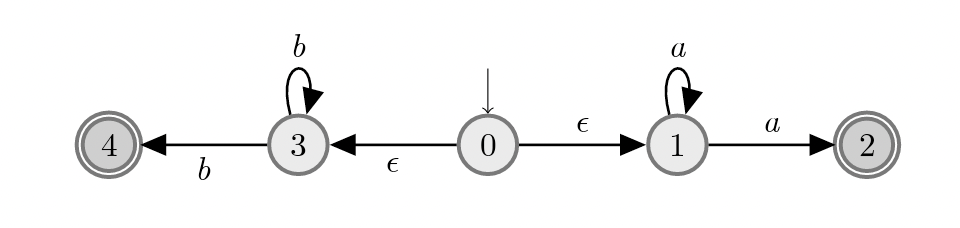
Exemple 6.1 Voici un exemple d’automate à deux états non déterministes sur l’alphabet \(\{a,b\}\). La relation de transition est \(\Delta=\{(0,a,0),(0,b,0),(0,a,1)\}\).

Figure 6.1: Un automate non déterministe.
Le non-déterminisme provient du fait qu’il y a deux arêtes qui partent de 0 avec l’étiquette \(a\).
Définition 6.2 Soit \((Q,\mathcal{A},i,\Delta,F)\) un automate non déterministe. Une éxécution d’un mot \(m=m_1\cdots m_n\in\mathcal{A}^*\) est suite d’états \((q_0,\dots,q_n)\) telle que pour tout \(i<n\) \((q_i,m_{i+1},q_{i+1})\in \Delta\) et \(q_0=i\).
Le mot \(m\) est reconnu ou accepté par l’automate s’il existe une éxécution \((q_0,\dots,q_n)\) de \(m\) telle que \(q_n\in F\).
Le langage reconnu par un automate non déterministe est l’ensemble des mots qu’il reconnaît.
Exemple 6.2 L’automate ci-dessus reconnait les mots qui terminent par un \(a\).
Remarque. Pour l’exemple de l’automate donné ci-dessus, il n’est pas très dur de trouver un automate déterministe qui reconnait le même langage.Par contre, si on considère \(L_k\) le langage sur \(\{a,b\}\) telle que la \(k\)-ième lettre en partant de la fin est un \(a\), il est très facile de trouver un automate non-déterministe qui reconnait \(L_k\) mais beaucoup plus dur de trouver un automate déterministe qui reconnait \(L_k\).
Définition 6.3 Soit \(A=(Q,\mathcal{A},i,\Delta,F)\) un automate non déterministe. L’automate déterminisé de \(A\) est l’automate déterministe \((\mathcal{P}(Q),\mathcal{A},\{i\},\delta, \mathcal{F})\) où
- \(\mathcal{P}(Q)\) est l’ensemble des parties de \(Q\),
- \(\delta\) est la fonction définie par \(\delta(X,a)=\{q', \exists q\in X, (q,a,q')\in\Delta\}\),
- \(\mathcal{F}=\{X\in\mathcal{P}(Q), X\cap F\neq\emptyset\}\).
On note cet automate déterministe \(\det(A)\).
Remarque. En pratique, cet automate déterministe a beaucoup plus d’état que \(A\). En effet si \(A\) a \(n\) états alors \(\det(A)\) en a \(2^n\). En particulier, si on part d’un automate déjà déterministe alors on ne retrouve pas l’automate initial.
Proposition 6.1 Soit \(A\) un automate non-déterministe. Les langages reconnus par \(A\) et \(\det(A)\) sont identiques, c’est-à-dire
\[\mathcal{L}(A)=\mathcal{L}(\det(A)).\]
Preuve. Soit \(m=m_1\dots m_n\) un mot reconnu par \(A\), alors il existe une éxécution \(q_0,\dots,q_n\) qui aboutit à un état final (\(q_n\in F\)). Ainsi \(\{q_0\},\dots\{q_n\}\) est une éxécution qui aboutit à un état final pour \(\det(A)\).
Réciproquement si \(X_0,\dots,X_n\) est une éxécution qui aboutit à un état final pour \(\det(A)\) alors en choisissant \(q_n\in X_n\cap F\) puis par récurrence \(q_{n-i}\) dans \(X_{n-i}\) tel que \((q_{n-i},m_{n-i+1},q_{n-i+1})\in\Delta\), on obtient \(q_0,\dots,q_n\) qui est une éxécution acceptante de \(m\) dans \(A\).
Remarque. La présence de l’ensemble vide dans les états de \(\det(A)\) fait que cet automate est toujours complet. L’état \(\emptyset\) joue le rôle du puit dans l’automate complété.
6.2 Automates non-déterministes asynchrones
Définition 6.4 Un automate non déterministe asynchrone est un quintuplé \((Q,\mathcal{A},i,\Delta,F)\) où
- \(Q\) est un ensemble fini d’états,
- \(\mathcal{A}\) est un alphabet,
- \(i\in Q\) est l’état initial,
- \(\Delta\subset Q\times \mathcal{A}\cup\{\varepsilon\}\times Q\) est la relation de transition et
- \(F\subset Q\) est l’ensemble des états finaux
On parle aussi d’automates avec \(\varepsilon\)-transitions.
La notion de mots reconnus et de langage reconnu s’étend naturellement avec l’idée qu’on peut “sauter” d’un état à un autre s’il sont reliés par une \(\varepsilon\)-transition.
Définition 6.5 Soit \(A=(Q,\mathcal{A},i,\Delta,F)\) un automate asynchrone, l’automate synchrone associé est \(sync(A)=(Q,\mathcal{A},i,\Delta',F')\) où \((q,a,q')\in\Delta'\) si on peut lire le mot \(\varepsilon^ks\varepsilon^l\) pour aller de \(q\) à \(q'\) dans \(A\) et \(F'\) est l’ensemble des états coaccessibles depuis \(F\) avec des \(\varepsilon\)-transitions.
Proposition 6.2 Les langages reconnus par \(A\) et \(sync(A)\) sont les mêmes.
En conclusion, les langages reconnus par des automates asynchrones non déterministes sont les mêmes que ceux reconnus par les automates déterministes.