Chapitre 3 Opérations sur les automates
Dans ce chapitre, nous voyons des opérations (algorithmiques) qui permettent à partir d’un ou plusieurs automates reconnaissant des langages \(L_1\) (éventuellement \(L_2\) aussi) de construire un nouvel automate \(A\) reconnaissant un langage \(L'\) construit par opérations ensemblistes sur \(L_1\) et \(L_2\).
On commence tout d’abord par construire un automate complet qui reconnaît le même langage qu’un automate déterministe non complet.
3.1 Complétion d’un automate déterministe
Définition 3.1 (équivalence de deux automates) On dit que deux automates \(A\) et \(A'\) sont équivalents s’ils reconnaissent le même langage, c’est-à-dire \(\mathcal{L}(A)=\mathcal{L}(A')\).
Proposition 3.1 Pour tout automate déterministe, il existe un automate déterministe complet équivalent.
Preuve. Soit \(A=(Q,i,\mathcal{A},\delta,F)\) un automate déterministe. On définit un nouvel état \(p\) comme “puit” et qui n’appartient pas à \(Q\), on définit \(A'=(Q',i,\mathcal{A},\delta',F)\) un nouvel automate où \(Q'=Q\cup\{p\}\) et \(\delta'(q,a)=\delta(q,a)\) si \(\delta(q,a)\) est déjà défini sinon on pose \(\delta'(q,a)=p\) et \(\delta'(p,a)=p\) pour tout \(a\in\mathcal{A}\).
L’automate \(A'\) est bien un automate déterministe complet car la fonction \(\delta'\) est bien définie sur tout \(Q\times\mathcal{A}\).
Il reste à voir que les deux automates reconnaissent bien le même langage.
Soit \(m=a_1a_2\dots a_n\) un mot sur \(\mathcal{A}\). Supposons que \(m\) soit reconnu par \(A\). Cela signifie qu’il existe une suite d’états \(q_0,q_1,\dots,q_n\in Q\) tels que \(q_0=i\) est l’état initial \(q_i+1=\delta(q_i,a_{i+1})\) pour tout \(0\leq i<n\) et \(q_n\in F\). On a donc aussi \(q_0,q_1,\dots,q_n\in Q'\) tels que \(q_0=i\) est l’état initial \(q_{i+1}=\delta'(q_i,a_{i+1})\) pour tout \(0\leq i<n\) et \(q_n\in F\). Donc \(m\) est bien reconnu par \(A'\).
Réciproquement si \(m\) est reconnu par \(A'\) alors l’éxécution de l’automate correspondante ne passe pas par \(p\) le puit, sinon l’éxécution aboutirait au puit mais le puit n’est pas un état final. Ainsi, il existe une suite d’états \(q_0,q_1,\dots,q_n\in Q'\backslash\{p\}\) tels que \(q_0=i\) est l’état initial \(q_i+1=\delta'(q_i,a_{i+1})\) pour tout \(0\leq i<n\) et \(q_n\in F\). Comme tous les \(q_i\) sont distincts de \(p\), on a alors \(q_i+1=\delta(q_i,a_{i+1})\) pour tout \(0\leq i<n\) et \(q_n\in F\). Ainsi, \(m\) est reconnu par \(A\).
En conclusion \(\mathcal{L}(A)=\mathcal{L}(A')\).
Exemple 3.1

Figure 3.1: Un graphe déterministe non complet qui reconnait les mots commençant par 111.
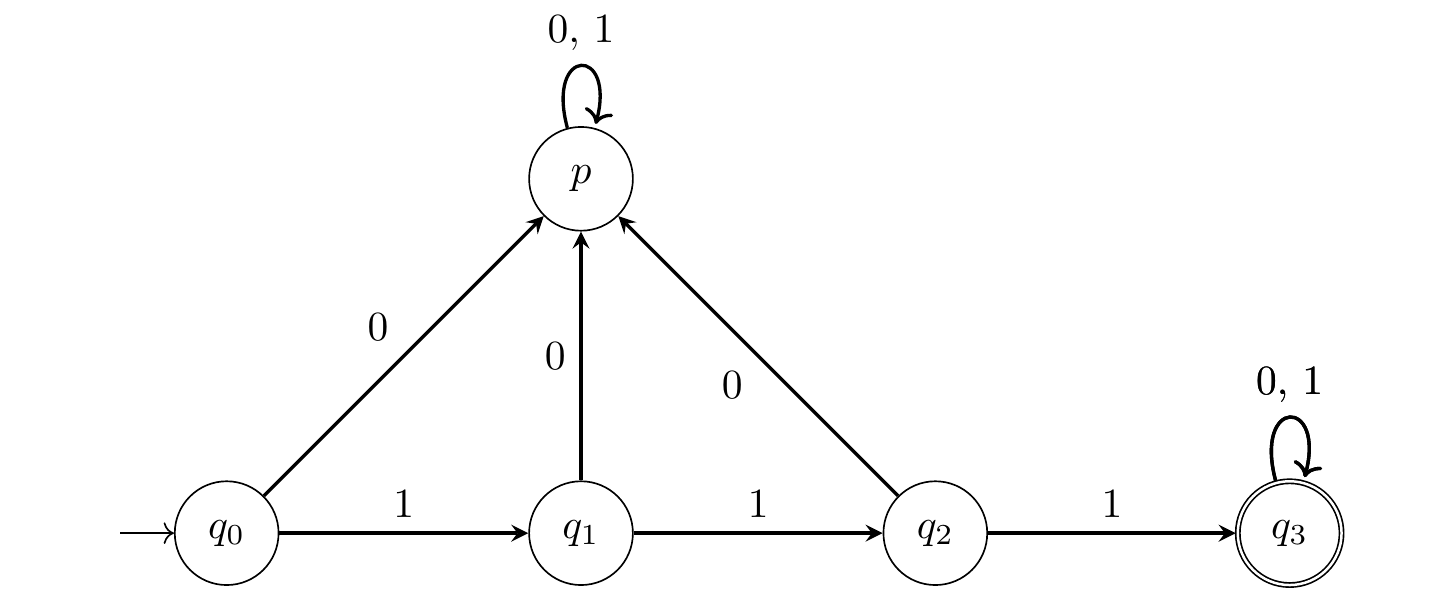
Figure 3.2: Un graphe déterministe complet qui reconnait aussi les mots commençant par 111.
Remarque. Si on applique cette complétion à un automate qui était déjà complet, on va simplement ajouter un état \(p\) qui ne sera relié à aucun autre.
3.2 Émondage
Émonder verbe transitif (bas latin emundare, nettoyer, purifier). Soumettre un arbre à l’émondage. Synonymes : ébrancher - élaguer - tailler
Un automate peut posséder des états non accessibles ou non coaccessibles. Ces états sont inutiles pour la reconnaissance des mots, on peut donc les retirer et obtenir un automate émondé qui reconnaît le même langage. Littéralement, on retire les branches mortes.
Proposition 3.2 Pour tout automate déterministe il existe un automate émondé équivalent.
Preuve. Soit \(A=(Q,i,\mathcal{A},\delta,F)\) un automate déterministe. Si \(i\) n’est pas coaccessible alors \(\mathcal{L}(A)=\emptyset\). Dans ce cas, il suffit de prendre pour \(A'\) l’automate émondé suivant :

Sinon comme \(i\) est toujours accessible, il y a au moins un état accessible et coaccessible. On définit alors \(A'=(Q',i,\mathcal{A},\delta',F')\) où
- \(Q'\) est l’ensemble des états accessibles et coaccessible,
- \(\delta'\) est la restriction de \(\delta\) à \(Q'\times\mathcal{A}\),
- \(F'=Q'\cap F\).
Tous les états de \(A'\) sont accessibles et coaccessibles car ils l’étaient déjà dans \(A\). Ainsi \(A'\) est émondé. Un mot est reconnu par \(A\) si et seulement si une éxécution aboutit à un sommet final et passe donc seulement par des états accessibles et coaccessibles. Un tel mot est reconnu par \(A'\) si et seulement s’il est reconnu par \(A\).
Remarque. Si on émonde un automate complet, l’automate obtenu n’est plus nécessairement complet. Par exemple, si on a complété un automate non complet, on a rajouté un puit qui est un état jamais coaccessible. Lors de l’émondage, cet état est retiré.
3.3 Reconnaissance du langage complémentaire
Rappelons que si \(L\) est un langage sur un alphabet \(\mathcal{A}\), le langage complémentaire \(L^c\) est l’ensemble des mots sur \(\mathcal{A}\) qui ne sont pas dans \(L\).
Proposition 3.3 Si \(A\) est un automate déterministe qui reconnaît un langage \(L\) alors il existe un automate \(A'\) qui reconnait le langage complémentaire \(L^c\).
Preuve. On commence par remplacer \(A\) par un automate \(A_1=(Q,i,\mathcal{A},\delta,F)\) complet qui reconnaît le même langage grâce à la Proposition 3.1.
Comme \(A_1\) est complet, pout tout \(m=a_1\dots a_n\), il existe une exécution de l’automate avec des états \(q_0,\dots,q_n\) où \(q_0=i\) et \(q_{j+1}=\delta(q_j,a_{j+1})\) pour \(j<n\). Le mot \(m\) est reconnu si et seulement \(q_n\in F\). Ainsi, avec l’automate \(A'=(Q,i,\mathcal{A},\delta,Q\backslash F)\), le mot \(m\) est reconnu par \(A'\) si et seulement s’il n’est pas reconnu par \(A_1\), c’est-à-dire \(m\notin \mathcal{L}(A)\). Au final, \(\mathcal{L}(A')=\mathcal{L}(A)^c\).
Remarque. Dans la preuve, il est important de commencer par compléter l’automate sinon les mots qui ne donnent pas d’éxécution de l’automate ne seront reconnus ni par \(A\) ni par \(A'\).
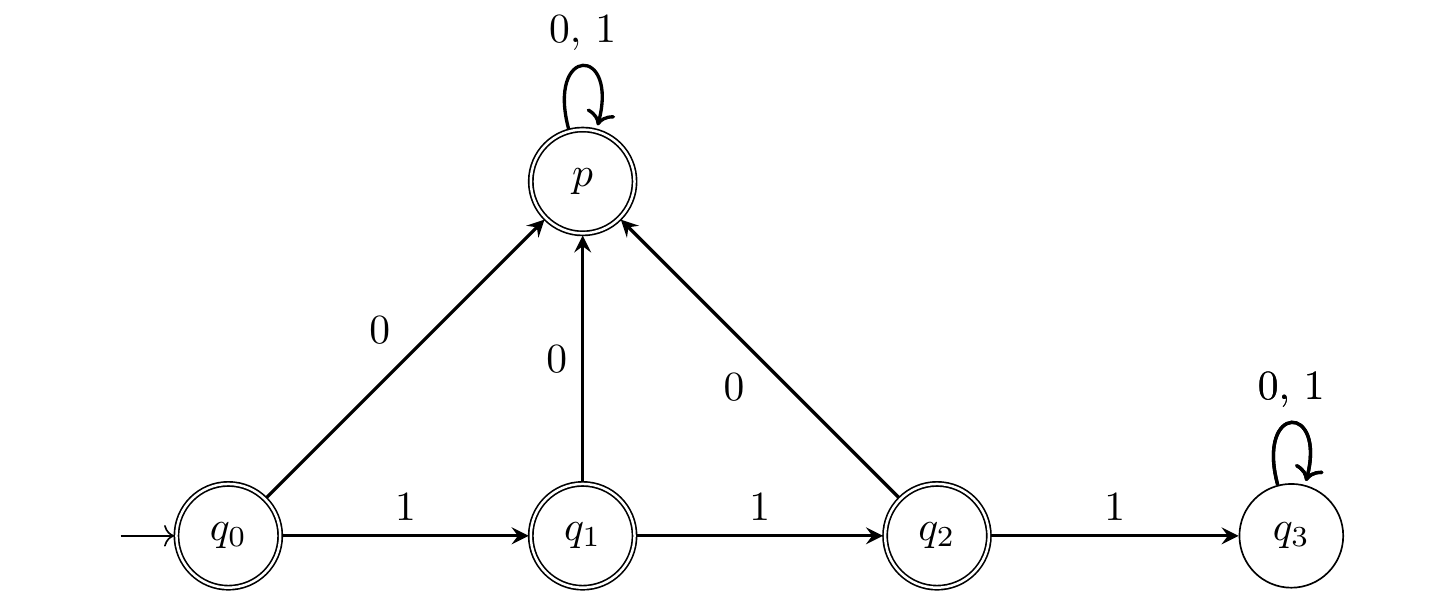
Figure 3.3: Un graphe déterministe complet qui reconnait aussi les mots qui ne commençent pas par 111.
3.4 Reconnaissance de l’intersection de deux langages
Définition 3.2 (automate produit) Soit \(A_1=(Q_1,i_1,\mathcal{A},\delta_1,F_1)\) et \(A_2=(Q_2,i_2,\mathcal{A},\delta_2,F_2)\) deux automates sur le même alphabet \(\mathcal{A}\).
L’ automate produit \(A_1\times A_2\) est l’automate \(A=(Q,i,\mathcal{A},\delta,F)\) où
- \(Q=Q_1\times Q_2\),
- \(i=(i_1,i_2)\),
- \(\delta((q_1,q_2),a)=(\delta_1(q_1,a),\delta_2(q_2,a))\) si \(\delta_1(q_1,a),\delta_2(q_2,a)\) sont bien définis,
- \(F=F_1\times F_2\).
Proposition 3.4 Soit \(L_1\) et \(L_2\) deux langages sur un même alphabet \(\mathcal{A}\) reconnus par des automates déterministes \(A_1\) et \(A_2\). L’automate produit \(A_1\times A_2\) reconnait l’intersection \(L_1\cap L_2\).
Preuve. Un mot \(m=a_1\dots a_n\) appartient à \(L_1\cap L_2\) si et seulement s’il existe deux suites d’états \(q_0^1,\dots,q_n^1\in Q_1\) et \(q_0^2,\dots,q_n^2\in Q_2\) telles que \(\delta_k(q_j^k,a_{j+1})=q_{j+1}\), et \(q^k_n\in F_k\) pour tout \(j<n\), \(k=1,2\).
Si \(A=A_1\times A_2\) comme dans la Définition 3.2, alors on a exactement que \(m\) est accepté par \(A\) si et seulement si \[\delta((q^1_j,q^2_j),a_{j+1})=(q^1_{j+1},q^2_{j+1})\] et \((q^1_{j+1},q^2_{j+1})\in F=F_1\times F_2\), c’est-à-dire si et seulement si \(m\) est accepté par \(A_1\) et \(A_2\).
Ainsi, \(\mathcal{L}(A_1\times A_2)=\mathcal{L}(A_1)\cap\mathcal{L}(A_2)\).
On obtient immédiatement la stabilité de la classe des langages reconnaissables par intersection finie.
Corollaire 3.1 Si \(L_1\) et \(L_2\) sont deux langages reconnaissables alors \(L_1\cap L_2\) l’est aussi.
3.5 Reconnaissance de l’union de deux langages
On a aussi stabilité de la classe des langages reconnaissables par union finie.
Proposition 3.5 Soit \(L_1\) et \(L_2\) deux langages reconnaissables alors \(L_1\cup L_2\) est aussi un langage reconnaissable.
Preuve. On utilise la propriété ensembliste suivante : pour deux sous-ensembles \(E,F\) d’un même ensemble, \((F\cap E)^c=F^c\cup E^c\).
Ainsi pour deux langages \(L_1,L_2\), \(L_1\cup L_2=(L_1^c\cap L^c_2)^c\). Donc si \(L_1\) et \(L_2\) sont reconnaissables alors \(L_1^c\) et \(L_2^c\) sont reconnaissables par la Proposition 3.3. Ainsi \(L_1^c\cap L_2^c\) est reconnaissable par la Proposition 3.4 et en conclusion \(L_1\cup L_2=(L_1^c\cap L^c_2)^c\) est reconnaissable par la Proposition 3.3 de nouveau.
3.6 Exercices
Exercice 3.1 Écrire en pseudo-code un algorithme qui prend en entrée un automate déterministe et retourne en sortie un automate déterministe complet qui reconnait le même langage.
Exercice 3.2 Soit \(L\) un langage sur un alphabet \(\mathcal{A}\). On définit le langage des préfixes de \(L\) de la manière suivante :
\[\operatorname{Pre}(L)=\{m\in\mathcal{A}^*,\ \exists m'\in L,m''\in \mathcal{A}^*,\ m'=m\cdot m''\}.\]
- Montrer que si \(L\) est un langage reconnaissable alors \(\operatorname{Pre}(L)\) aussi.
- Peut-on faire la même chose pour les suffixes ?
Exercice 3.3 Reprendre les automates de l’Exercice 3.5 et pour chacun d’eux donner
- L’automate complété (s’il n’est pas déjà complet)
- L’automate reconnaissant le langage complémentaire
Exercice 3.4 On considère les deux automates \(A_1\) et \(A_2\) suivants
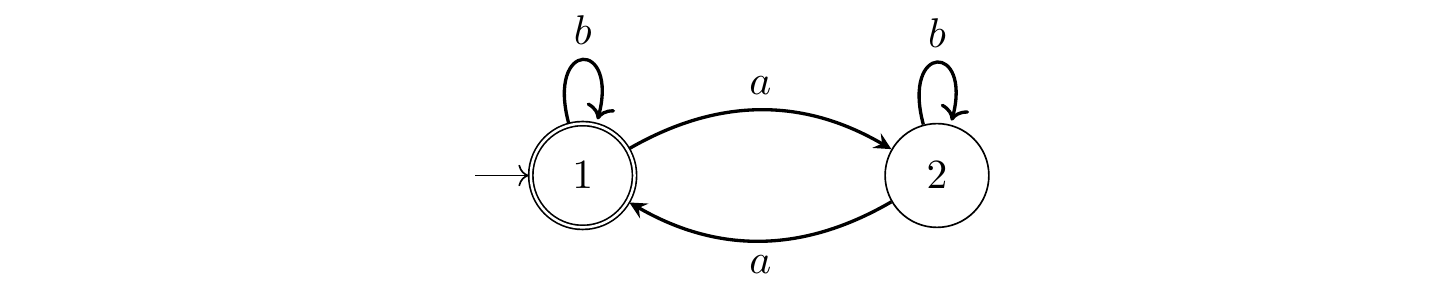
Figure 3.4: Automate \(A_1\).

Figure 3.5: Automate \(A_2\).
- Décrire les langages \(L_1\) et \(L_2\) reconnus par \(A_1\) et \(A_2\).
- Construire l’automate produit \(A_1\times A_2\).
- Quel est le langage reconnu par \(A_1\times A_2\) ?
- Construire un automate qui reconnait \(L_1\cup L_2\).
Exercice 3.5 Soit \(L\) un langage reconnaissable sur un alphabet \(\mathcal{A}\).
- Montrer que le langage \(L'\) constitué de mots de \(L\) de longueur paire est aussi reconnaissable.
- Soit \(a\in\mathcal{A}\). Montrer que le langage \(L''\) des mots de \(L\) qui ne contiennent pas \(a\) est aussi reconnaissable.
Exercice 3.6 Soit \(A_1\) et \(A_2\) deux automates complets. L’automate \(A_1\times A_2\) est-il complet ?
Exercice 3.7 Donner un automate émondé qui reconnait le même langage que l’automate suivant.
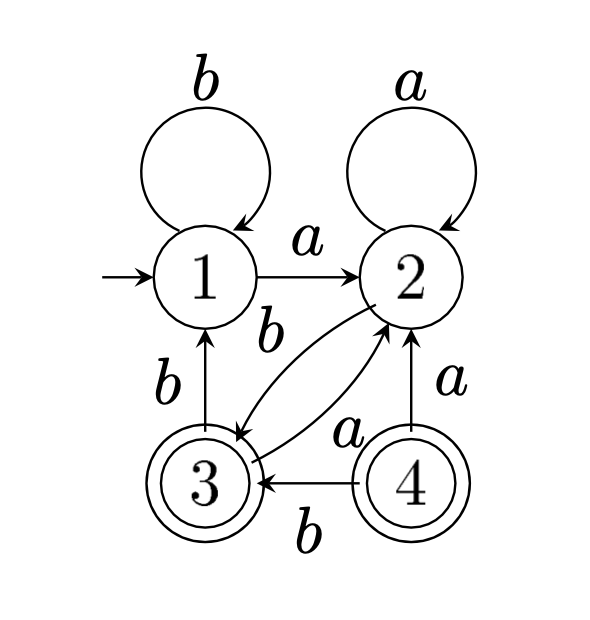
Figure 3.6: Automate à émonder.