Chapitre 7 Expressions régulières

7.1 Expressions régulières

Commençons par la définition des expressions et leur syntaxe, c’est-à-dire la manière dont on peut les combiner. Cette définition des expressions régulières est inductive dans le sens où l’on donne des expressions élementaires puis on indique comment on en construit de nouvelles avec certaines opérations algébriques (\(*,+,\cdot\)) auxquelles on peut de nouveau appliquer ces constructions pour obtenir toutes les expressions régulières.

Définition 7.1 (Expressions régulières) Soit \(\mathcal{A}\) un alphabet. L’ensemble des expressions régulières \(ER(\mathcal{A})\) est l’ensemble des expressions obtenues de la manière suivante :

  • Les symboles de \(\mathcal{A}\), \(\emptyset\) et \(\varepsilon\) sont des expressions régulières.
  • Si \(e,e'\) sont des expressions régulières alors \(e\cdot e'\) et \(e+e'\) sont des expressions régulières.
  • Si \(e\) est une expression régulière alors \(e^*\) est aussi une expression régulière.

Remarque. 1.Lorsque plusieurs opérateurs (\(*,+,\cdot\)) sont utilisés, il est important de savoir dans quel ordre ils sont appliqués et pour cela on utilise des parenthèses. 2.Le symbole de concaténation est usuellement oublié et compris implicitement. 3.On utilise les mêmes règles d’associativité pour l’opérateur \(+\) : \((a+b)+c=a+(b+c)\) et on note simplement \(a+b+c\). 4.On applique les règles de priorité dans cette ordre : L’étoile \(*\) est priorité sur la multiplication (concaténation) \(\cdot\) qui est elle-même prioritaire sur l’addication \(+\).

Par exemple, \(a_1a_2^*+bc\) signifie \((a_1\cdot(a_2^*))+(b\cdot c)\).

Remarque. Si on voulait formaliser cette définition, les expressions régulières seraient des mots sur l’alphabet \(\mathcal{A}\cup\{\emptyset,\varepsilon,(,)\}\). Leur ensemble forme donc un langage sur cet alphabet.

À une expression régulière, on associe un langage, c’est-à-dire que l’on donne un sens à cette expression régulière, c’est la sémantique des expressions régulières.

Définition 7.2 (Langage associé à une expression régulière) Soit \(\mathcal{A}\) un alphabet. À une expression régulière \(e\), on associe un langage \(\mathcal{L}(e)\) de la manière inductive suivante :

  • \(\mathcal{L}(\emptyset)=\emptyset\),
  • \(\mathcal{L}(\varepsilon)=\{\varepsilon\}\),
  • \(\mathcal{L}(a)=\{a\}\) pour tout \(a\in\mathcal{A}\),
  • \(\mathcal{L(e_1+e_2)}=\mathcal{L}(e_1)\cup\mathcal{L}(e_2)\) pour deux expressions régulières \(e_1,e_2\).
  • \(\mathcal{L(e_1e_2)}=\mathcal{L}(e_1)\cdot\mathcal{L}(e_2)\) pour deux expressions régulières \(e_1,e_2\).
  • \(\mathcal{L}(e^*)=\mathcal{L}(e^*)\) pour toute expression régulière \(e\).

Exemple 7.1 Sur l’alphabet \(\{0,1\}\), Le langage reconnu par l’expression régulière \[(0+1)^*(0^*10^*10^*)(0+1)^*\] est l’ensemble des mots contenant au moins deux \(1\).

Définition 7.3 (Équivalence d'expressions régulières) Soit \(e_1,e_2\) deux expressions régulières sur le même alphabet. Ces expressions sont équivalentes si \(\mathcal{L}(e_1)=\mathcal{L}(e_2)\).

En particulier, si on a deux expressions régulières équivalentes, on a intérêt à choisir la plus simple (c’est-à-dire la plus courte) et à remplacer la plus compliquée par la plus simple partout où elle apparaît.

Remarque. L’équivalence entre deux expressions régulières forment bien une relation d’équivalence sur l’ensemble des expressions régulières.

Définition 7.4 (Langage régulier) Soit \(\mathcal{A}\) un alphabet. Un langage \(L\) sur \(\mathcal{A}\) est régulier s’il est existe une expression régulière \(e\) sur \(\mathcal{A}\) telle que \(L=\mathcal{L}(e)\).

Dans ce cas, on dit que \(L\) est reconnu par l’expression \(e\).

Remarque. La similarité entre les opérations pour les expressions régulières et les opérations algébriques fait que l’on parle aussi de langage rationnel au lieu de langage régulier.

7.2 Théorème de Kleene

Le théorème suivant fait le lien entre automates et expressions régulières. Il nous dit exactement que les langages reconnus par des automates sont les mêmes que les automates reconnus par des expressions régulières.

Théorème 7.1 (Théorème de Kleene) Soit \(\mathcal{A}\) un alphabet et \(L\) un langage. Le langage \(L\) est reconnaissable si et seulement s’il est régulier.

Pour démontrer ce théoèreme, il faut et il suffit de montrer qu’à tout automate on peut associer une expression régulière qui reconnaît le même langage et récipropquement qu’à toute expression régulière, on peut associer un automate (qui en pratique sera non déterministe et asynchrone) qui reconnaît le même langage.

Nous verrons deux méthodes algorithmiques pour cela.

7.2.1 Des automates aux expressions régulières

Il existe plusieurs méthodes pour associer une expression régulière à un automate. Celle que nous voyons est la méthode d’élimination des états qui est la plus simple à mettre en oeuvre mais a le défaut de produire des expressions régulières qui ne sont pas toujours les plus simples.

Pour appliquer cette méthode, il est nécessaire de partir d’un automate normalisé.

Définition 7.5 (automate normalisé) Un automate non-déterministe asynchrone est normalisé si l’état initial n’a aucune transition entrante et s’il y a un unique final et que celui n’a aucune transition sortante.

Proposition 7.1 (Normalisation) Pour tout automate, il existe un automate normalisé équivalent.

Preuve. Soit \(A\) un automate (non-déterministe asynchrone), On construit un automate normalisé de la manière suivante \(A'\) de la manière suivante.

  1. Si l’état initial \(i\) a une transition entrante, on ajoute un état \(i_0\) qui devient l’état initial et on ajoute une \(\varepsilon\)-transition \(i\to i_0\).
  2. S’il y a plusieurs états finaux ou s’il y a une transition sortante d’un état final, on ajoute un nouvel état \(f\) qui devient le seul état final et on ajoute des \(\varepsilon\)-transitions des états finaux sortants vers \(f\).

On vérifie que \(\mathcal{L}(A)=\mathcal{L}(A')\).

Voici maintenant l’algorithme d’association d’une expression régulière à un automate normalisé \(A=(Q,\mathcal{A},i,\Delta,f)\).

Fonction \(R\colon Q\times Q\to ER(\mathcal{A})\)
   Pour \(q\in Q\)
       Pour \(q'\in Q\)
           \(R(q,q')=\sum_{(q,s,q')\in\Delta}s\)
       Fin Pour
   Fin Pour
Tant Que \(Q\neq\{i,f\}\)
   Choisir \(q\in Q\neq\{i,f\}\)
   Pour \(q_1\in Q\backslash\{i,f\}\)
       Pour \(q_2\in Q\backslash\{i,f\}\)
\(R ( q_1 ,q_2 ) = R ( q_1 ,q_2 )+ R ( q_1 ,q ) · R ( q, q )^∗ · R ( q, q_2 )\)
       Fin Pour
   Fin Pour
   \(Q=Q\backslash\{q\}\)
FinTantQue
Retourne \(R(i,f)\)

7.2.2 Des expressions régulières aux automates

Voyons maintenant comment créer un automate équivalent à partir d’une expression régulière. De nouveau, il en existe plusieurs et celle présentée ici est la méthode compositionnelle.

On commence pour cela par associer un automate aux expressions régulières à un caractère : \(\emptyset,\varepsilon, a\in\mathcal{A}\).

  1. Pour \(\emptyset\), on associe l’automate \(A_\emptyset\)
  2. Pour \(a\in \mathcal{A}\cup\{\varepsilon\}\), on associe l’automate \(A_a\)

Maintenant, supposons que l’on ait deux expressions \(e_1\) et \(e_2\) auxquelles on a associé deux automates \(A_1\) et \(A_2\).

  1. À l’expression \(e_1+e_2\), on associe l’automate suivant (où les carrés representent tout un automate)
  2. À l’expression \(e_1e_2\), on associe l’automate suivant
  3. À l’expression \(e_1^*\), on associe l’automate suivant

7.3 Exercices

Exercice 7.1 On considère l’alphabet \(\{a,b,c\}\). Dans chaque cas donner une expression régulière qui reconnait le langage suivant.

  1. Les mots qui commencent par \(a\) et finissent par \(b\).
  2. Les mots qui contiennent au moins trois fois \(a\).
  3. Les mots tels que tout \(a\) est suivi d’un \(b\).
  4. Les mots tels que tout \(a\) n’est jamais suivi d’un \(c\).
  5. Les mots qui contiennent un nombre pair de \(a\).
  6. Les mots de longueur impaire.
  7. Les mots dont le nombre de \(a\) est divisible par 3.
  8. Les mots qui ne contiennent pas \(aa\).
  9. Les mots qui contiennent deux \(a\) mais non consécutifs.
  10. Les mots qui commencent et finissent par le même symbole.

Exercice 7.2 Pour les expressions régulières suivantes donner le langage reconnu par l’expression réguilère.

  1. \(a(a+b)^*b\)
  2. \(a^*bab^*\)
  3. \((a+ba)^*\)
  4. \(a^*+b^*\)
  5. \(((a+b^*)b)^*\)
  6. \((a^*+b^*)^*\)
  7. \((a+b+c)^*abc(a+b+c)^*\).

Exercice 7.3 Dire si les paires d’expressions régulières suivantes sont équivalentes où \(R\) et \(S\) désignent deux expressions régulières.

  1. \((\varepsilon+R)^*\) et \(R^*\)
  2. \((\varepsilon+R)R^*\) et \(R^*\)
  3. \((R+S)^*\) et \(R^*+S^*\)
  4. \((RS+R)^*R\) et \(R(SR+R)^*\)
  5. \((RS+R)^*RS\) et \((RR^*S)^*\)
  6. \((R+S)^*S\) et \((R^*S)^*\)
  7. \(S(RS+S)^*R\) et \(RR^*S(RR^*S)^*\).

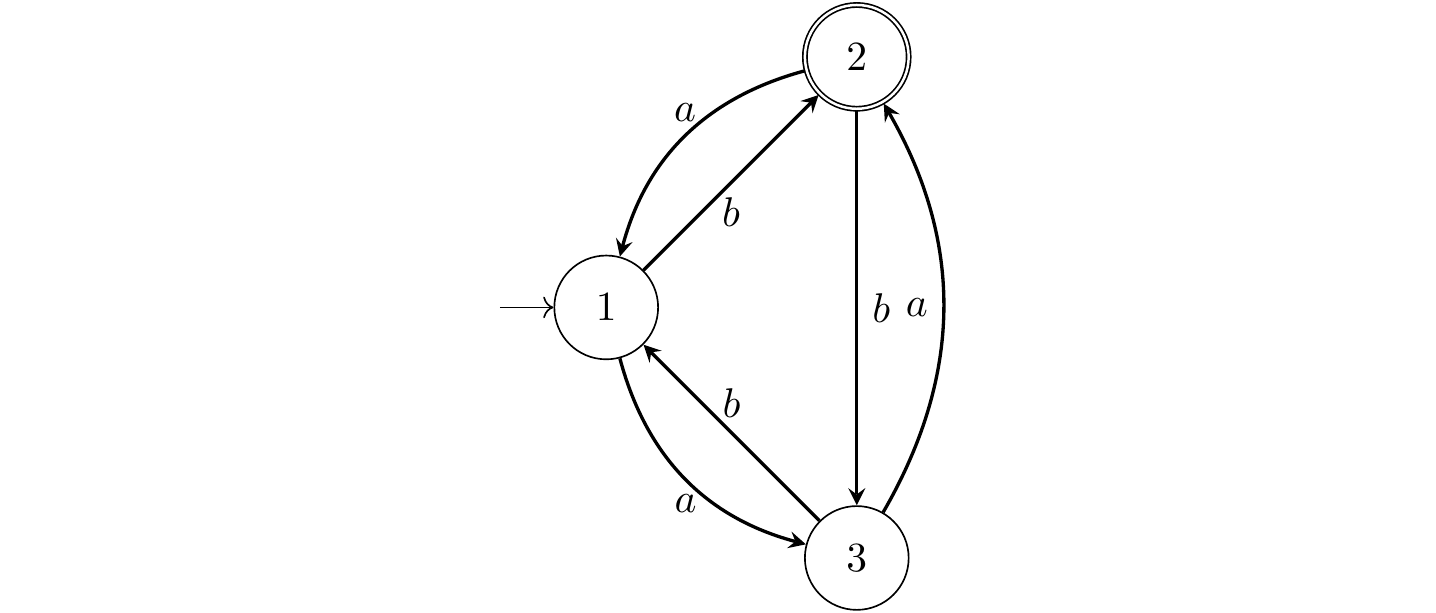
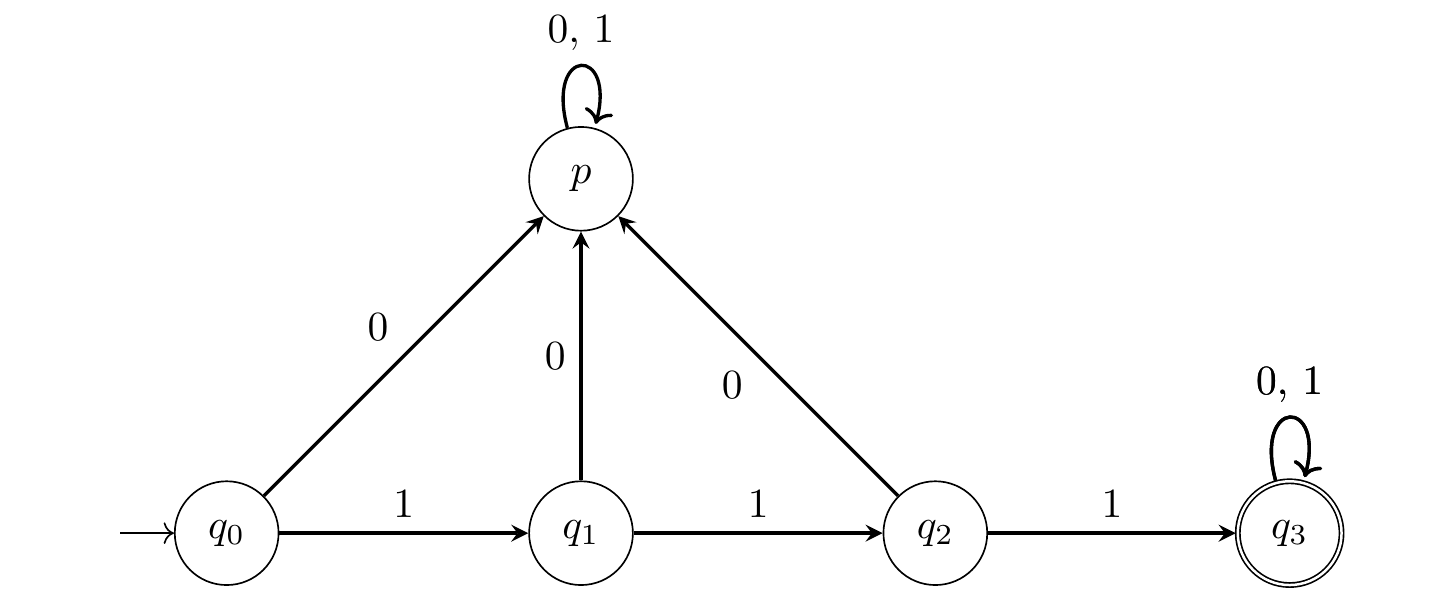
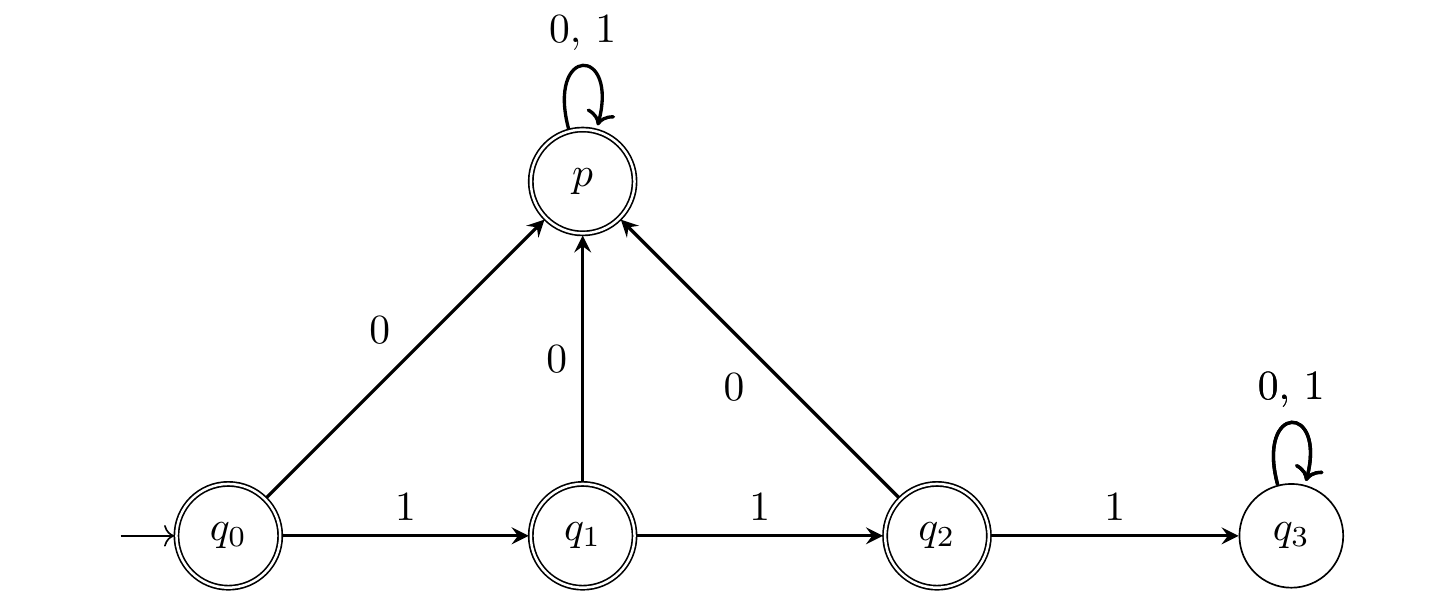
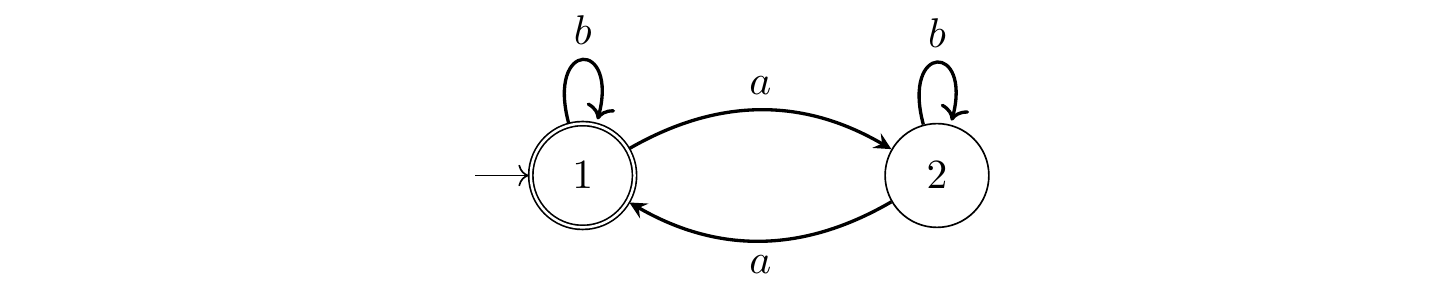
Exercice 7.4 Pour les automates suivants, trouver une expression régulière qui reconnait le même langage.

Exercice 7.5 Trouver un automate qui reconnait le même langage que les expressions suivantes sur l’alphabet \(\{a,b\}\).

  1. \(a\cdot b\) .
  2. \(a^∗\cdot b\).
  3. \(( a + b )^∗\cdot a\) .
  4. \(a^∗\cdot b + a \cdot ( a + b )^∗\).