Chapitre 2 Automates déterministes

Dans ce chapitre, on introduit une première définition d’automates, ce seront les automates finis déterministes. Nous verrons plus tard des automates plus généraux et les automates déterministes apparaitront comme cas particulier.

2.1 Automates finis déterministes

Définition 2.1 Soit \(X,Y\) deux ensembles. On dit que \(f\colon X\to Y\) est une fonction partielle s’il existe \(X'\subseteq X\) tel que \(f\) est une fonction de \(X'\) vers \(Y\) est une fonction. Si \(X'=X\), on que dit que \(f\) est totale (c’est-à-dire que \(f(x)\) est défini pour tout \(x\in X\)).

Remarque. Une fonction partielle totale est donc simplement une fonction…

Définition 2.2 (automate fini déterministe) Un automate fini déterministe est un quintuplé \((Q,\mathcal{A},i,\delta,F)\) où

\(Q\) est un ensemble fini dont les éléments sont appelés états
\(\mathcal{A}\) est un alphabet
\(i\in Q\) est l’ état initial
\(\delta\colon Q\times\mathcal{A}\to Q\) est une fonction partielle appelée fonction de transition.
\(F\subseteq Q\) est l’ensemble des états finaux.

Remarque. Dans la définition d’automate fini déterministe, le terme fini se réfère au fait que l’ensemble des états \(Q\) est fini. Il existe aussi des automates à ensemble d’états infini mais nous ne les traiterons pas dans ce cours. Ainsi, on parlera simplement d’automate pour automate fini.

Remarque. Le terme déterministe se réfère au fait qu’étant dans un état donné, lorsqu’on lit une lettre \(a\in\mathcal{A}\), on peut aller dans au plus un autre état. Ce qui signifie que pour tout \((q,a)\in Q\times\mathcal{A}\), il existe au plus un \(q'\in Q\) tel que \(\delta(q,a)=q'\).

Définition 2.3 Un automate déterministe est complet si sa fonction de transition \(\delta\) est totale, c’est-à-dire que \(\delta\colon Q\times \mathcal{A}\to Q\) est une fonction.

Définition 2.4 (représentation graphique) À tout automate déterministe \((Q,\mathcal{A},i,\delta,F)\), on associe un graphe orienté étiqueté.

Les sommets sont les états
Les arcs sont les paires \((q,q')\)
Pour un arc \((q,q')\), on ajoute comme étiquette l’ensemble \(E_{q,q'}\) des symboles \(a\) tels que \(\delta(q,a)=q'\).
L’état initial est indiqué par un arc qui arrive à cet état mais ne provenant pas d’un autre état.
Les états finaux sont entourés d’un double cercle

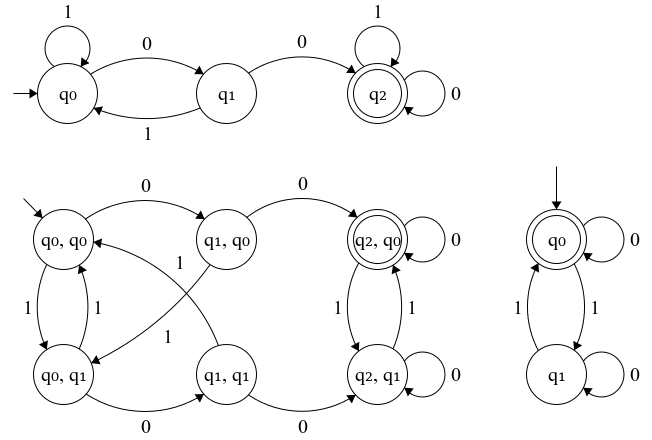
Figure 2.1: Quelques exemples d automates.

Définition 2.5 (représentation tabulaire) À tout automate déterministe \((Q,\mathcal{A},i,\delta,F)\), on associe un tableau dont les lignes sont indicées par les états et les colonnes par les symboles. À l’intersection de la ligne \(q\) et de la ligne \(a\), on trouve (s’il existe) l’état \(q'\) tel que \(\delta(q,a)=q'\).

Définition 2.6 (configuration) Une configuration d’un automate déterministe \((Q,\mathcal{A},i,\delta,F)\) est une paire \((q,m)\) où \(q\) est un état et \(m\in\mathcal{A}^*\) est un mot.

Définition 2.7 (relation de dérivation) On introduit la relation de dérivation notée \(\to\) entre deux configurations \((q,m)\) et \((q',m')\) par

\[(q,m)\to (q',m')\iff \exists a\in\mathcal{A}, m=a\cdot m' \wedge \delta(q,a)=q'.\]

Définition 2.8 (exécution d'un automate) L’exécution d’un mot \(m\) à partir d’un état \(q\) est la suite de configurations \((q_0,m_0),\dots,(q_n,m_n)\) où \(m_0=m\), \(q_0=q\), \(n=|m|\) et pour tout \(j\leq n-1\),

\[(q_i,m_i)\to(q_{i+1},m_{i+1}).\]

Remarque. On dit aussi calcul réalisé par automate pour éxécution d’un automate.

2.2 Langage reconnu par un automate

Définition 2.9 (mot accepté par un automate) Soit \(A=(Q,\mathcal{A},i,\delta,F)\) un automate déterministe et \(m\in \mathcal{A}^*\). On dit que \(m\) est accepté par \(A\) s’il existe une éxécution \((q_0,m_0),\dots,(q_n,m_n)\) avec \(q_0=i\), \(m_0=m\) et \(q_n\in F\), \(m_n=\varepsilon\).

Définition 2.10 (langage reconnu par un automate) Soit \(A=(Q,\mathcal{A},i,\delta,F)\) un automate déterministe. Le langage reconnu est l’ensemble des mots sur \(\mathcal{A}\) accepté par \(A\). On le note \(\mathcal{L}(A)\).

Définition 2.11 (classe des langages reconnaissables) Un langage \(L\) est reconnaissable s’il existe un automate fini déterministe \(A\) tel que \(L=\mathcal{L}(A)\).

Remarque. On parle aussi de langage à états finis pour parler de langage reconnaissable par un automate fini.

2.3 Fonction de transition étendue

Définition 2.12 (fonction de transition étendue) Soit \(A=(Q,\mathcal{A},i,\delta,F)\) un automate déterministe, la fonction de transition étendue est la fonction partielle \(\delta^*\) définie sur \(Q\times \mathcal{A}^*\) de manière récursive par

\(\delta^*(q,\varepsilon)=q\)
\(\delta^*(q,a\cdot m)=\delta^*(\delta(q,a),m)\)

Remarque. Par abus de notation on notera simplement \(\delta\) au lieu de \(\delta^*\). Cela ne posera pas de problème, car pour tout \(a\in\mathcal{A}\), \(\delta^*(q,a)=\delta(q,a)\).

2.4 Accessibilité et coaccessibilité

Définition 2.13 (sommet accessible) Soit \(A=(Q,\mathcal{A},i,\delta,F)\) un automate déterministe. Un sommet \(q\in Q\) est accessible s’il existe un mot \(m\) tel que \(\delta(i,m)=q\).

Définition 2.14 (sommet coaccessible) Soit \(A=(Q,\mathcal{A},i,\delta,F)\) un automate déterministe. Un sommet \(q\in Q\) est coaccessible s’il existe un mot \(m\) tel que \(\delta(q,m)\in F\).

Définition 2.15 (automate déterministe émondé) Un automate déterministe est émondé si tous ses états sont accessibles et coaccessibles.

2.5 Exercices

Exercice 2.1 On considère l’alphabet \(\mathcal{A}=\{a,b\}\). Combien y a-t-il d’automates déterministes complets à 2 états ? À 3 états ? Les représenter (si vous êtes conrageux).

D’une manière générale, combien y a-t-il d’automates déterministes complets à \(n\) états ?

Exercice 2.2 Montrer que si \((q_0,m_0),\dots,(q_n,m_n)\) est une éxécution pour un automate \(A\) alors \(m_n=\varepsilon\). On pourra montrer par récurrence que \(|m_j|=n-j\).

Exercice 2.3 Pour un automate déterministe \(A=(Q,\mathcal{A},i,\delta,F)\), montrer qu’un mot \(m\) est accepté si et seulement si \(\delta(i,m)\in F\).

Exercice 2.4 Considérons l’alphabet \(\{ a, b \}\). Pour chacun des ensembles suivants, donner un automate fini déterministe qui reconnaît cet ensemble de mots, si cela est possible.

L’ensemble des mots avec un nombre d’occurrences du symbole \(a\) multiple de 2.
L’ensemble des mots avec un nombre d’occurrences du symbole \(a\) multiple de 3.
L’ensemble des mots avec exactement \(n\) occurrences du symbole \(a\) , pour un certain \(n\in\mathbb{N}\).
L’ensemble des mots avec \(n\) occurrences ou moins du symbole \(a\) , pour un certain \(n\in\mathbb{N}\).
L’ensemble des mots avec strictement plus de \(n\) occurrences du symbole \(a\), pour un certain \(n\in\mathbb{N}\).
L’ensemble des mots avec autant d’occurrences du symbole \(a\) que d’occurences du symbole \(b\).
L’ensemble des mots tels que chaque facteur de 3 symboles contienne exactement 2 occurrences du symbole \(a\).

Exercice 2.5 Pour les automates finis suivants sur l’alphabet \(\{a,b\}\), dire s’ils sont complets, construire la représentation tabulaire et décrire le langage reconnu par une propriété caractérisant ce langage.

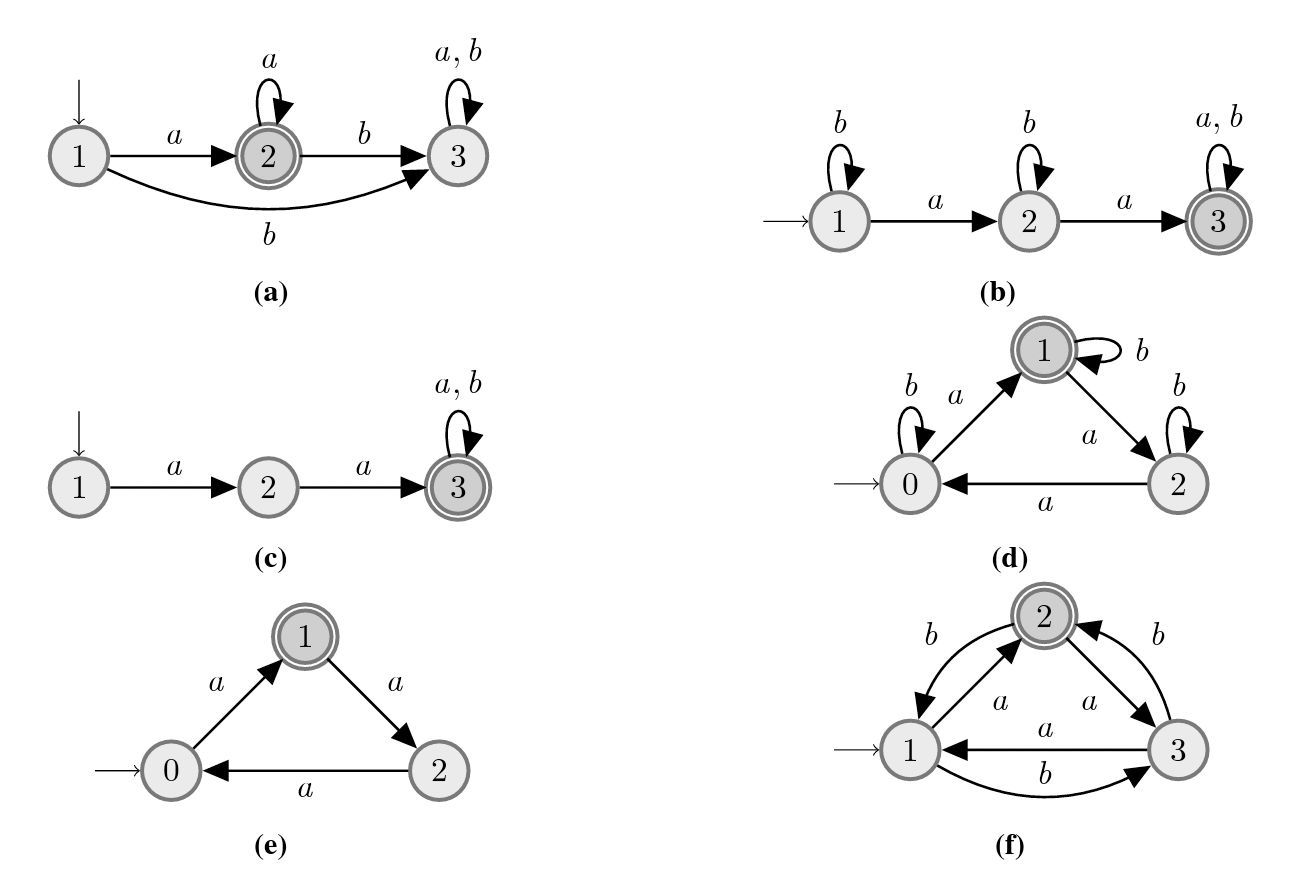
Figure 2.2: Quelques exemples d automates.

Exercice 2.6 Montrer que pour tout automate déterministe \(A\), il existe un automate déterministe complet \(A'\) tel que \(\mathcal{L}(A)=\mathcal{L}(A')\). On pourra pour cela ajouter un nouvel état appelé “puit” où aboutira les arcs avec les étiquettes qui n’existent pas dans \(A\).