Chapitre 1 Transformations géométriques

Dans ce cours, on ne considérera que l’espace vectoriel $\mathbf{R}^n$ et le plus souvent $n$ sera 2 ou 3. Pour toutes les transformations que nous allons introduire, dans la pratique nous aurons besoin de leurs inverses, c’est pourquoi nous donnerons sytématiquement l’inverse des transformations que nous étudierons.

1.1 Transformations linéaires

1.1.1 Homothéties

Définition 1.1 Soit $\lambda\in\mathbf{R}$, l’homothétie de rapport $\lambda$ est l’application linéaire

\[h_\lambda\colon\begin{matrix} \mathbf{R}^n&\to&\mathbf{R}^n\\\ v&\mapsto&\lambda v. \end{matrix}\]

L’homothétie de rapport $\lambda>0$ correspond à un changement d’échelles : toutes les longueurs sont multipliées par $\lambda$. La matrice d’une homothétie est particulièrement simple, et ceci dans n’importe quelle base $\mathcal{B}$ de $\mathbf{R}^n$:

\[\mathrm{Mat}_{\mathcal{B}}(h_\lambda)=\begin{bmatrix}\lambda&0&0\\0&\ddots&0\\0&0&\lambda\end{bmatrix}.\]

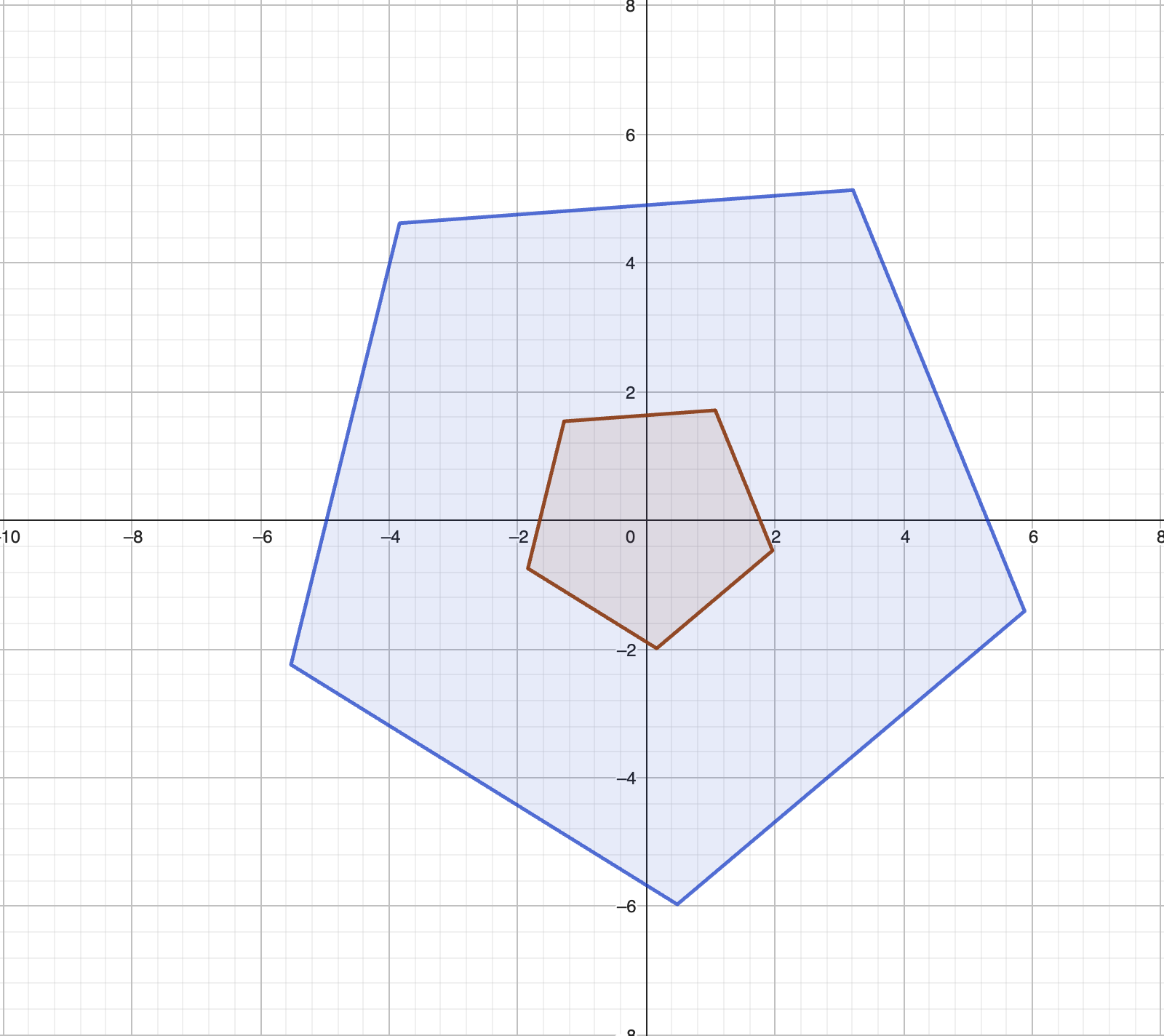
Figure 1.1: Un pentagone et son image par l’homothétie de rapport 3

Lemme 1.1 Si $\lambda\neq0$ alors $h_\lambda$ est inversible d’inversible $h_{\lambda^{-1}}$.

Preuve. Pour démontrer le résultat, il suffit d’observer que si $\lambda_1,\lambda_2\in\mathbf{R}$ alors $h_{\lambda_1}\circ h_{\lambda_2}=h_{\lambda_1\lambda_2}$ et que $h_1=\mathrm{id}$.

1.1.2 Rotations

Définition 1.2 En dimension 2, la rotation d’angle $\theta\in\mathbf{R}$ dans le sens trigonométrique est l’application linéaire associée à la matrice

\[R_\theta=\begin{bmatrix}\cos(\theta)&-\sin(\theta)\\\sin(\theta)&\cos(\theta))\end{bmatrix}.\]

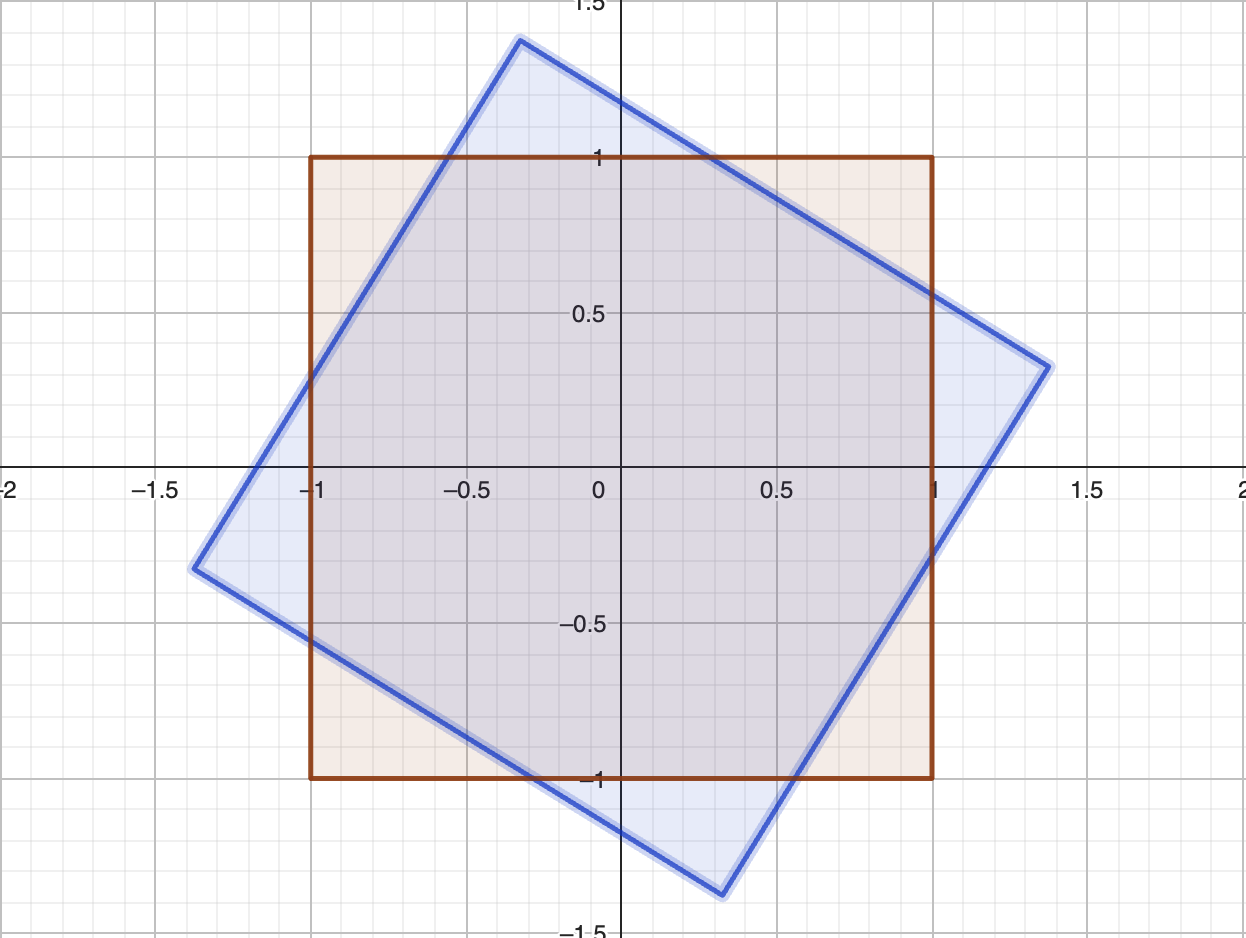
Figure 1.2: Un carré et son image par la rotation d’un huitième de tour

Proposition 1.1 Soit $A\in\mathrm{M}_2(\mathbf{R})$ orthogonale telle que $\det(A)=1$ alors il existe $\theta\in\mathbf{R}$ tel que $A=R_\theta$.

Preuve. Soit $A=\begin{bmatrix} a&b\\c& d\end{bmatrix}$ une telle matrice. Comme $A$ est orthogonale $^tAA=I_2$. Ainsi $a^2+b^2=1$, $c^2+d^2=1$, et $ac+bd=0$. Ainsi, il existe $\theta_1$ et $\theta_2$ tels que $a=\cos(\theta_1)$, $b=\sin(\theta_1)$, $d=\cos(\theta_2)$ et $\sin(\theta_2)$. Comme $ac+bd=0$, $\theta_1=\theta_2$ ou $\theta_1=-\theta_2$ (à un multiple entier de $2\pi$ près). Finalement, comme $ad-bc=1$, $\cos(\theta_1+\theta_2)=1$, on a $\theta_1=\theta_2$ et $A=R_{\theta_1}$.

Exemple 1.1 La matrice $\begin{bmatrix}\sqrt{2}/2&-\sqrt{2}/2\\ \sqrt{2}/2&\sqrt{2}/2\end{bmatrix}$ est orthogonale de déterminant 1. Il s’agit de la matrice $R_{\pi/4}$.

Exemple 1.2 La matrice $\begin{bmatrix} -1&0\\0&-1\end{bmatrix}$ est orthogonale de déterminant $1$. Il s’agit de la matrice $R_\pi$ aussi appelée symétrie centrale.

Définition 1.3 Soit $\mathcal{B}=(e_1,e_2,e_3)$ une base orthonormée de $\mathbf{R}^3$. La rotation d’axe $\mathrm{Vect}(e_1)$ et d’angle $\theta\in\mathbf{R}$ dans le sens direct est l’application linéaire donnée par la matrice

\[R_\theta=\begin{bmatrix}1&0&0\\0&\cos(\theta)&-\sin(\theta)\\0&\sin(\theta)&\cos(\theta)\end{bmatrix}\] dans la base $\mathcal{B}$.

Lemme 1.2 Si $\theta$ n’est pas un multiple entier de $2\pi$ alors l’axe de $R_\theta$ est l’espace propre associée à la valeur propre 1 de $R_\theta$.

Preuve. Puisque $R_\theta e_1=e_1$, on a $\mathrm{Vect}(e_1)\subseteq E_1$, l’espace propre associé à la valeur propre 1. D’autre part, si $(x,y,z)\in E_1$ alors $y=\cos(\theta)y-\sin(\theta)z$ et $z=\sin(\theta)y+\cos(\theta)z$, ce qui donne $(1-\cos(\theta))y=-\sin(\theta)z$ et $(1-\cos(\theta))z=\sin(\theta)y$. En multipliant la première égalité par $1-\cos(\theta)$ et en remplaçant $(1-\cos(\theta))z$ par $\sin(\theta)y$, on obtient $(1-\cos(\theta))^2=-\sin(\theta)^2$. Comme un carré n’est jamais strictement négatif, si $y\neq0$, on obtient $\sin(\theta)=0$ et $\cos(\theta)=1$, c’est-à-dire $\theta$ est un multiple entier de $2\pi$.

Ainsi $y=0$ et $z=0$. Donc $E_1=\mathrm{Vect}(e_1)$.

Rappelons que la trace d’une matrice carrée est la somme de ses coefficients diagonaux et que cette trace est invariante par changement de bases. Avec cette définition, on a immédiatement le résultat suivant.

Lemme 1.3 La trace de $R_\theta$ vaut $1+2\cos(\theta)$.

Lemme 1.4 Soit $A\in\mathrm{M}_n(\mathbf{R})$ une matrice orthogonale et $\lambda$ un vecteur propre alors $|\lambda|=1$.

Preuve. Soit $v$ un vecteur propre non nul pour $\lambda$. Alors $|\lambda|^2||v||^2=||Av||^2=||v||^2$ et comme $||v||\neq 0$, on a bien $\lambda=\pm 1$.

Théorème 1.1 Soit $A\in\mathrm{M}_3(\mathbf{R})$ orthogonale avec $\det(A)=1$ alors il existe $\mathcal{B}=(e_1,e_2,e_3)$ base orthonormée de $\mathbf{R}^3$ telle que la matrice de l’application linéaire associée à $A$ dans la base $\mathcal{B}$ soit $R_\theta$.

Preuve. Le degré du polynôme caractéristique de $A$ est 3 donc ce polynôme possède une racine, c’est-à-dire que $A$ possède une valeur propre $\lambda\in\mathbf{R}$. Par le Lemme 1.4, on sait que $\lambda=\pm 1$. Si $\lambda=-1$ alors $E_{-1}$ ne peut pas être de dimension 3 à cause du déterminant égal à 1. Si $E_{-1}$ a pour dimension 2 alors $E_{-1}^\bot$ est invariant par $A$ et de dimension donc c’est forcément l’homothétie de rapport 1. Ce qui implique qu’en changeant de base, la matrice de l’application est $\begin{bmatrix}1&0&0\\0&-1&0\\0&0&-1\end{bmatrix}$, ce qui correspond à $R_\pi$.

Si $\dim(E_{-1})=1$ alors la restriction de $A$ à $E_{-1}^\bot$ est une matrice orthogonale de déterminant $-1$ et on peut montrer que cette restriction possède aussi -1 comme valeur propre ce qui donne comme contradiction $dim(E_{-1})\geq 2$.

Maintenant si $\lambda=1$ alors la restriction de $A$ à $E_1^\bot$ est une matrice orthogonale de déterminant 1, il s’agit donc d’une rotation $R_\theta$. En concaténant une base orthonormée de $E_1$ et $E_1^\bot$, on a une base orthonormée de $\mathbf{R}^3$ dans laquelle la matrice de l’application linéaire associée à $A$ est $R_\theta$.

1.1.3 Symétries

Définition 1.4 Soit $f$ une application linéaire de $\mathbf{R}^2$. On dit que $f$ est une symétrie (orthogonale) s’il existe $\mathcal{B}$ base orthonormée de $\mathbf{R}^2$ telle que

\[\mathrm{Mat}_{\mathcal{B}}(f)=\begin{bmatrix}1&0\\0&-1\end{bmatrix}.\]

C’est-à-dire que si $(u_1,u_2)$ est une telle base alors $f(u_1)=u_1$ et $f(u_2)=-u_2$.

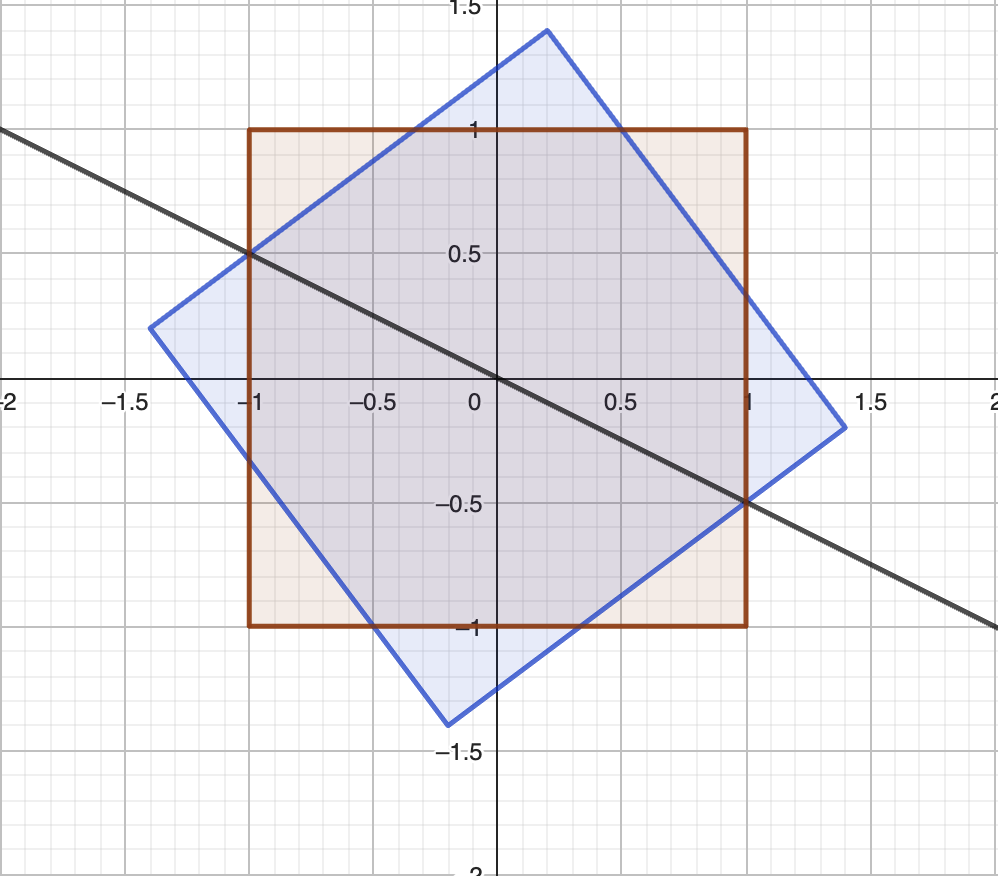
Figure 1.3: Un carré et son image par la symétrie par rapport à la droite d’équation x+2y=0

Théorème 1.2 Soit $A$ une matrice orthogonale de $\mathbf{R}^2$ telle que $\det(A)=-1$. Alors l’application linéaire associée à $A$ est une symétrie.

Preuve. Le début de la preuve est identique à celle du Théorème 1.1. Si $A=\begin{bmatrix} a&b\\c& d\end{bmatrix}$ alors on obtient l’existence de $\theta_1$ et $\theta_2$ tels que $a=\cos(\theta_1)$, $b=\sin(\theta_1)$, $d=\cos(\theta_2)$ et $c=\sin(\theta_2)$ mais maintenant, comme le déterminant vaut $-1$, on a $ad-bc=-1$, ce qui donne $\cos(\theta_1+\theta_2)=-1$ et donc $\theta_2=\pi-\theta_1$ (à un multiple de $2\pi$ près). Ainsi $d=-\cos(\theta_1)$. Ce qui impliqe que la trace de $A$ est nulle. Le calcul du polynôme caractéristique donne $(a-X)(d-X)-bc=X^2-(a+d)X+\det(A)=X^2-1$. Ce polynôme a deux racines : 1 et -1. Ainsi $-1$ et $1$ sont valeurs propres de $A$. Comme $A$ est orthogonale, on peut trouver une base orthogonale dans laquelle, la matrice de l’application linéaire associée est $\begin{bmatrix}1&0\\0&-1\end{bmatrix}.$

1.2 Transformations affines

1.2.1 Translations et transformations affines

Définition 1.5 Soit $u$ un vecteur de $\mathbf{R}^n$. La translation de vecteur $u$ est l’application $\tau_u\colon\mathbf{R}^n\to\mathbf{R}^n$ telle que pour tout $v\in \mathbf{R}^n$, $\tau_u(v)=u+v$.

Définition 1.6 Soit $f\colon\mathbf{R}^n\to\mathbf{R}^n$ une application. On dit que $f$ est affine, s’il existe $g\colon\mathbf{R}^n\to\mathbf{R}^n$ linéaire et $b\in\mathbf{R}^n$ tels que $f(v)=g(v)+b$, c’est-à-dire $f=\tau_b\circ g$.

L’application $g$ s’appelle la partie linéaire de $f$.

Remarque. Si $A$ est la matrice de l’application linéaire de $g$, avec le produit matriciel, on a $f(v)=Av+b$. On retrouve alors une expression semblable aux applications affines de dimension 1, c’est-à-dire les applications de la forme $f(x)=ax+b$.

1.2.2 homothéties rotations et symétries affines

Définition 1.7 Soit $f$ une application de $\mathbf{R}^n$ dans lui-même avec $n=2$ ou 3. On dit que $f$ est une homothétie, respectivement une rotation ou une symétrie affine si $f$ est une application affine et sa partie linéaire est une homothétie, respectivement une rotation ou une symétrie avec au moins un point fixe.

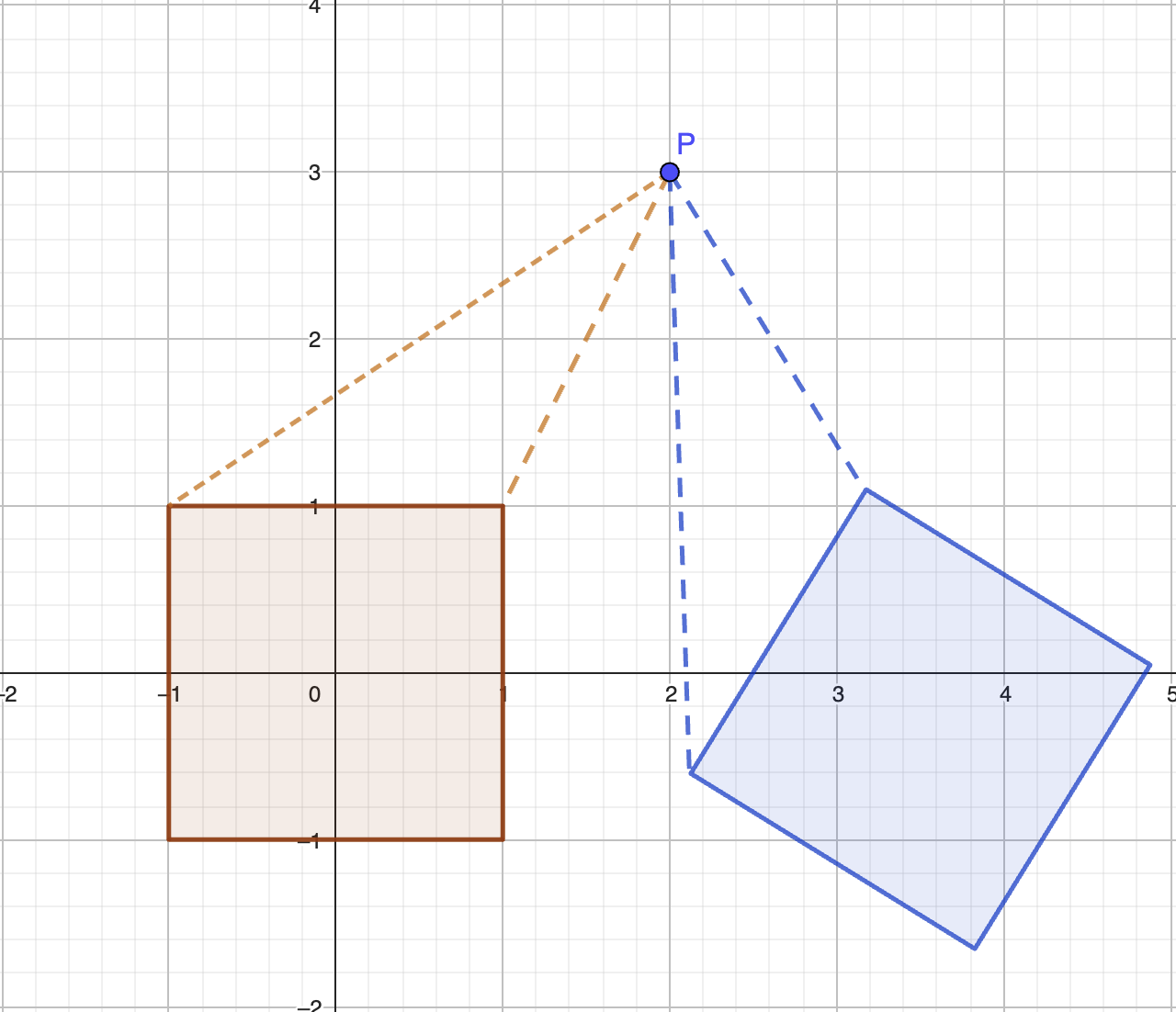
Figure 1.4: Un carré et son image par la rotation d’un huitième de tour et de centre P

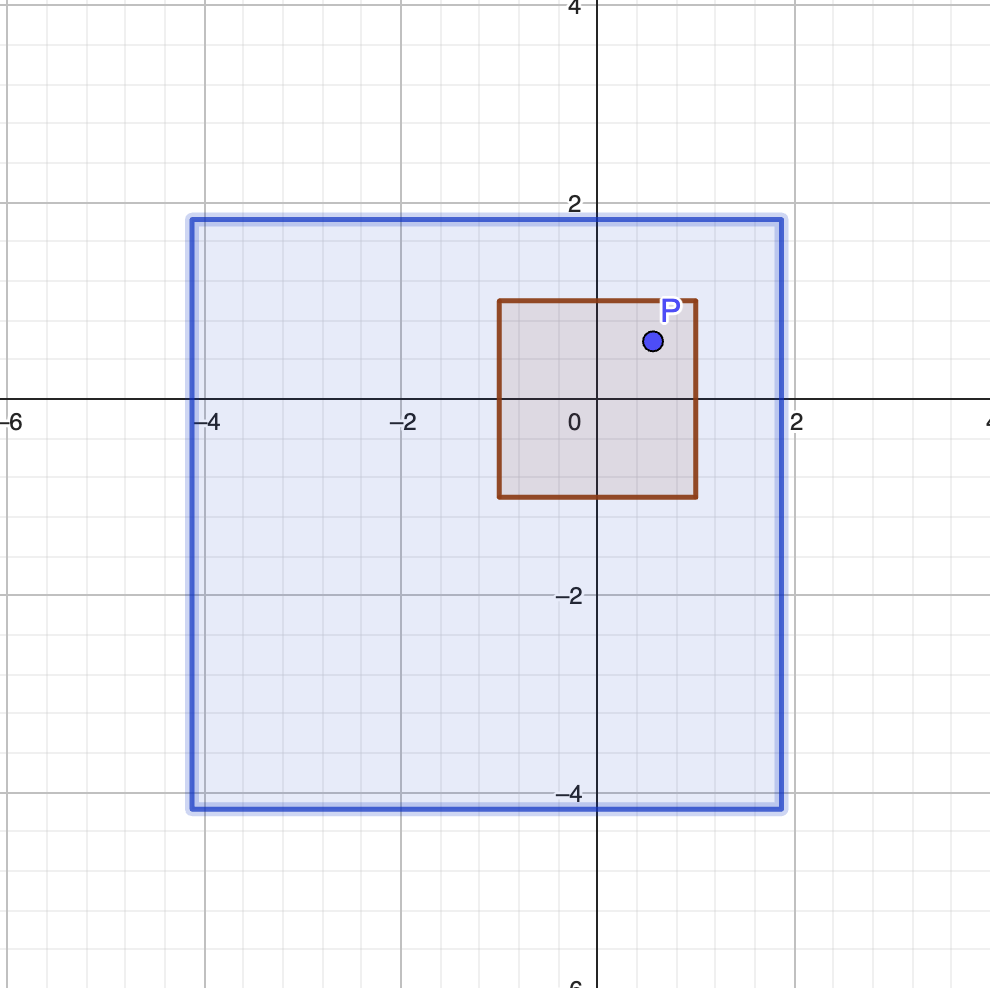
Figure 1.5: Un carré et son image par l’homothétie de rapport 3 centrée en P

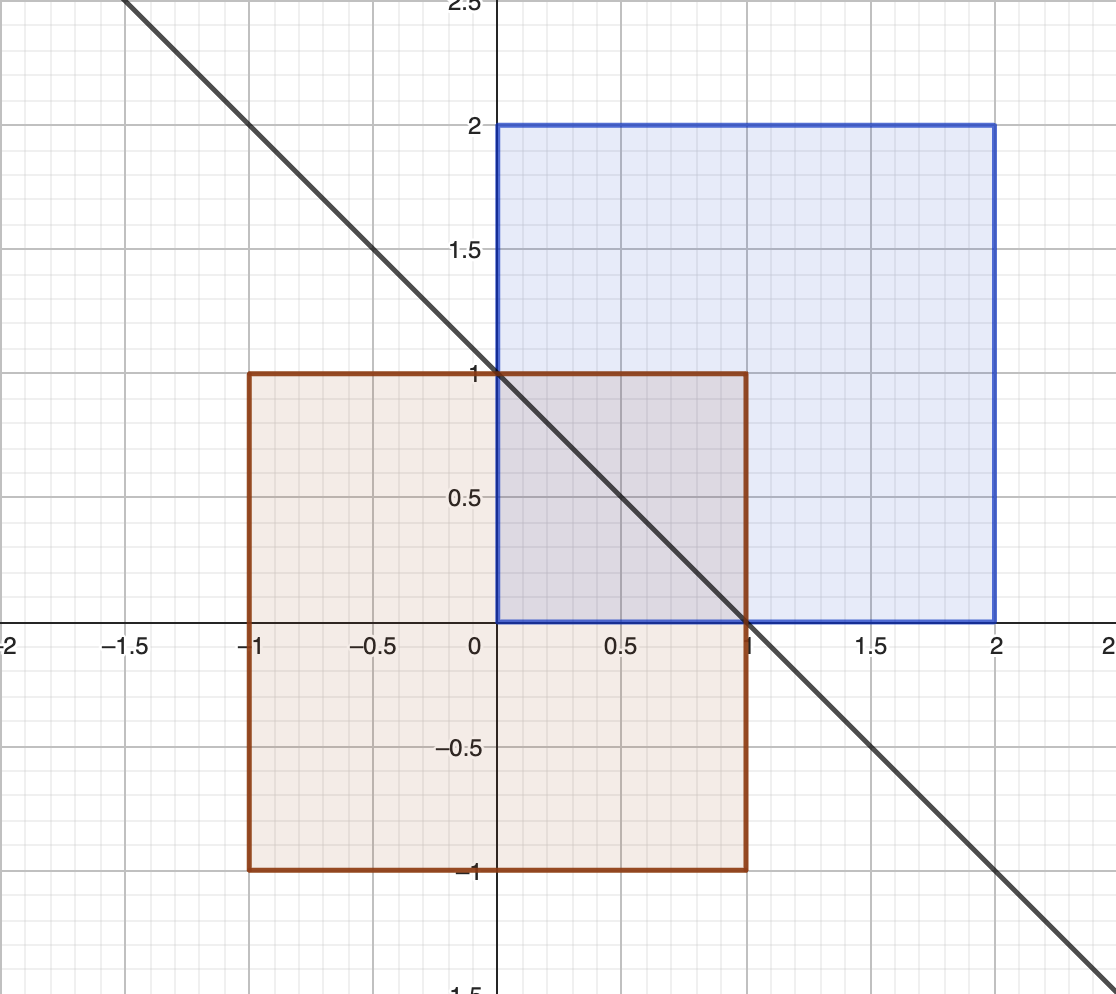
Figure 1.6: Un carré et son image par la symétrie par rapport à la droite d’équaiton x+y=1

Proposition 1.2 Toute rotation affine $R$ d’angle $\theta$ qui n’est pas un multiple de $2\pi$ possède un unique point fixe $c$ (c’est-à-dire avec $R(c)=c$). L’application $R$ est $\tau_c\circ R_0\circ \tau_{-c}$ où $R_0$ est la partie linéaire de $R$.

Remarque. Dans l’énoncé, on se permet d’identifier un point $P$ de $\mathbf{R}^2$ avec le vecteur $\overrightarrow{OP}$.

Preuve. On cherche à résoudre l’équation $R(c)=c$ or $R(c)=R_0c+u$ ce qui donne $(Id-R_0)c=u$. Or $Id-R_0$ est une application linéaire inversible car 1 n’est pas valeur propre de $R_0$. Ainsi $c=(Id-R_0)^{-1}u$ qui est l’unique point fixe.

Maintenant vérifions que $R=\tau_c\circ R_0\circ \tau_{-c}$. Calculons $\tau_c\circ R_0\circ \tau_{-c}(v)=R_0(v-c)+c=R_0v+(c-R_0c)$. C’est-à-dire que $\tau_c\circ R_0\circ \tau_{-c}= \tau_{c-R_0c}\circ R_0$ mais avec $c=R(c), on a $u=c-R_0c$ et donc on retrouve $\tau_c\circ R_0\circ \tau_{-c}=R$.

Proposition 1.3 Toute homothétie affine $h$ de rapport $\lambda\neq1,0$ possède un unique point fixe $c$ ($h(c)=c$) appelé centre et $h=\tau_c\circ h_\lambda\circ \tau_{-c}$.

Preuve. Il s’agit essentiellement d’adapter la preuve donnée pour les rotations.

Proposition 1.4 Toute symétrie affine possède une droite affine (c’est-à-dire ne passant pas forcément par 0) de points fixes appelée axe de symétrie.

Preuve. Par définition une symétrie $S$ possède au moins un point fixe $p$. Soit $S_0$ sa partie linéaire et soit $E_1$ l’espace associée à la valeur propre 1. On sait que $S$ est de la forme $S(v)=S_0(v)+u$ pour un certain $u\in\mathbf{R}^2$. Donc $p$ vérifie $u=p-S_0(p)$. Maintenant si $q\in\mathbf{R}^2$ vérifie $q-p\in E_1$ alors $S(q)=S_0(q)+u=S_0(q-p+p)+u=S_0(q-p)+S_0(p)+u=q-p+p-u+u=q$ et donc $q$ est aussi fixe. Ainsi toute la droite $p+E_1$ est une droite affine de points fixes.

Proposition 1.5 Soit $S$ une symétrie affine d’axe d’équation $ax+by=c$ alors

\[S\begin{pmatrix}x\\ y\end{pmatrix}=\begin{pmatrix}x\\ y\end{pmatrix}-2\frac{ax+by-c}{a^2+b^2}\begin{pmatrix}a\\ b\end{pmatrix}.\]

1.3 Exercices

Exercice 1.1 On considère la matrice $\begin{bmatrix}\sqrt{3}/2&-1/2\\1/2&\sqrt{3}/2\end{bmatrix}$. Justifier qu’il s’agit d’une matrice de rotation et identifier son angle.

Exercice 1.2 On considère la matrice $A=\begin{bmatrix}\sqrt{2}/2&\sqrt{2}/2\\\sqrt{2}/2&-\sqrt{2}/2\end{bmatrix}$.

Justifier qu’il s’agit d’une matrice de symétrie.
Donner une base $\mathcal{B}=(u_1,u_2)$ dans laquelle l’application linéaire associée à $A$ a pour matrice $\begin{bmatrix}1&0\\0&-1\end{bmatrix}$.
Calculer la matrice de passage $P$ de la base canonique vers $\mathcal{B}$ et son inverse puis vérifier que $P^{-1}AP=\begin{bmatrix}1&0\\0&-1\end{bmatrix}$.

Exercice 1.3 Soit $A$ la matrice $\begin{bmatrix}0&1&0\\0&0&1\\1&0&0\end{bmatrix}$. Justifier que $A$ est une rotation. Trouver son axe et son angle non-orienté, (c’est-à-dire entre 0 et 180° ) $\theta$ puis donner une base orthonormée de $\mathbf{R}^3$ dans laquelle $A=R_\theta$.

Exercice 1.4 Donner l’expression de la rotation d’angle $\pi/3$ et de centre $(1,2)$ dans les coordonnées canoniques $(x,y)$ de $\mathbf{R}^2$.

Exercice 1.5 Donner l’expression de l’homothétie de centre $(1,1)$ et de rapport 2 dans les coordonnées canoniques $(x,y)$ de $\mathbf{R}^2$.

Exercice 1.6 Donner l’expression de la symétrie d’axe la doite $x+y=2$ dans les coordonnées canoniques $(x,y)$ de $\mathbf{R}^2$.

Exercice 1.7 On considère une homothétie linéaire $h_\lambda$ avec $\lambda\neq0,1$ et $\tau_u$, la translation de vecteur $u$. Est-ce que $h_\lambda\circ \tau_u=\tau_u\circ h_\lambda$ ?

Exercice 1.8 On considère l’application suivante de $\mathbf{R}^2$ :

\[\begin{pmatrix}x\\ y\end{pmatrix}\mapsto \begin{pmatrix}\frac{\sqrt{3}}{2} x-\frac{1}{2}y+\frac{5-2\sqrt{3}}{2}\\\frac{1}{2}x+\frac{\sqrt{3}}{2} y-\frac{\sqrt{3}}{2}\end{pmatrix}.\]

Justifier qu’il s’agit d’une transformation affine.
Reconnaître la transformation dont il s’agit, donner sa partie linéaire.
Trouver son centre.

Exercice 1.9 On considère l’application suivante de $\mathbf{R}^2$ :

\[\begin{pmatrix}x\\ y\end{pmatrix}\mapsto \begin{pmatrix}\frac{\sqrt{3}}{2} x+\frac{1}{2}y+\frac{1-\sqrt{3}}{2}\\\frac{1}{2}x-\frac{\sqrt{3}}{2} y+\frac{1+\sqrt{3}}{2}\end{pmatrix}.\]

Justifier qu’il s’agit d’une transformation affine.
Reconnaître la transformation dont il s’agit, donner sa partie linéaire.
Trouver son axe et en donner l’équation cartésienne.

Exercice 1.10 Donner les inverses des transformations suivantes :

Rotation de centre $p$ et d’angle $\theta$.
Homothétie de rapport $\lambda$ et de centre $p$.
Symétrie d’axe $D$.