Chapitre 2 Géométrie projective

2.1 Introduction

La géométrie projective donne un cadre formel à la géométrie de la vision. Elle est à la base de la représentation en deux dimensions des scènes en trois dimensions. Son développement a été initié par la technique de perspective utilisée en peinture.

Figure 2.1: Gravure sur bois d’Albrecht Dürer montrant l’utilisation de la géométrie projective en dessin.

De nos jours, elle est utilisée de manière intensive dans des logiciels d’animation 3D comme Blender. Notre but est de comprendre un peu comment fonctionne la perspective et les changements de perspective.

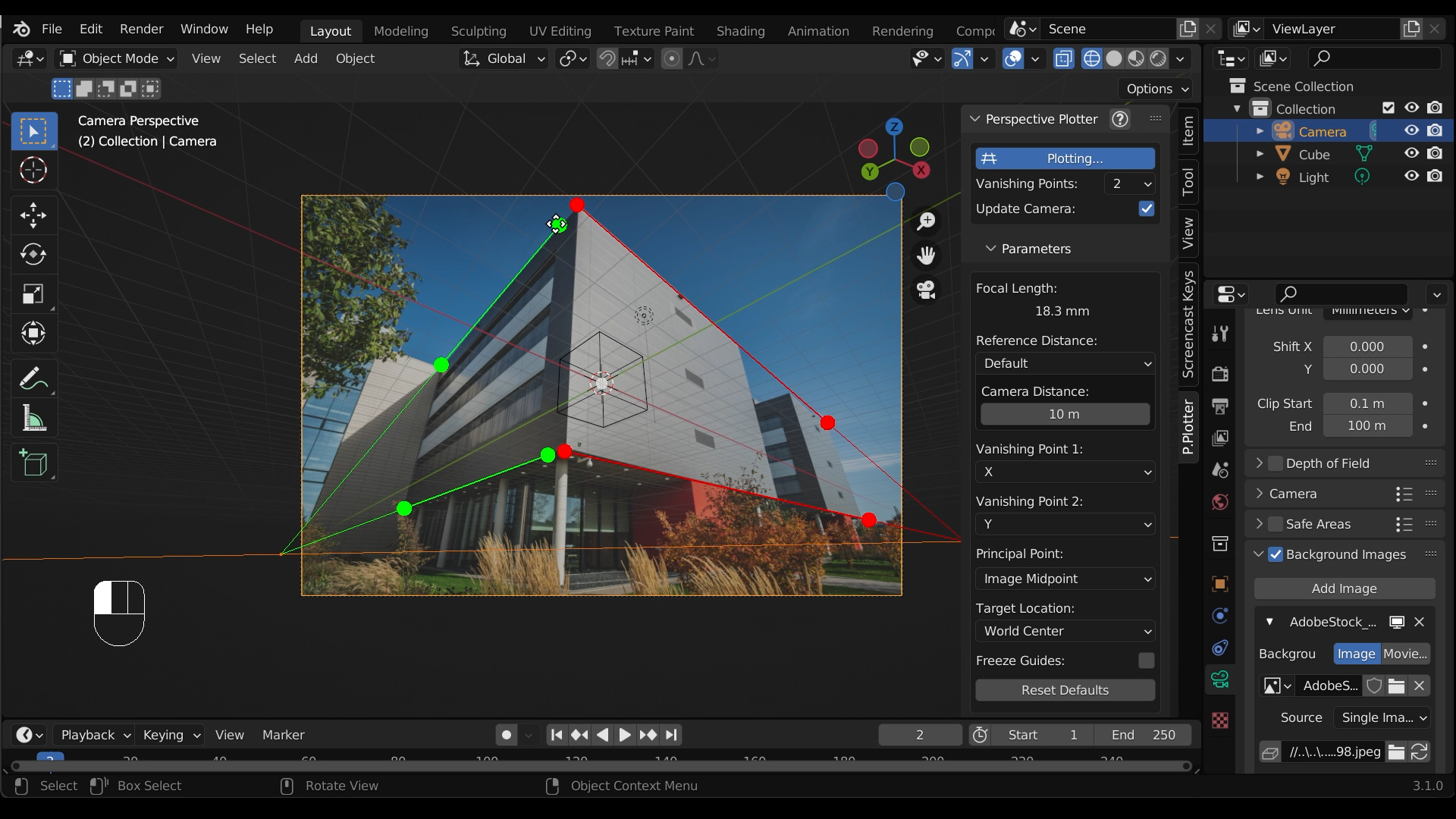
Figure 2.2: Blender et son module de perspective.

2.2 Projection et perspectives

Définition 2.1 Le plan projectif est l’ensemble des droites vectorielles de \(\mathbf{R}^3\). On le note \(\mathbf{P}_2\).

Définition 2.2 Soit \(v\in \mathbf{R}^3\setminus\{0\}\), on note \(p(v)\in\mathbf{P}_2\) la droite vectorielle engendrée par \(x\).

On rappelle que la droite vectorielle engendrée par \(x\neq0\) est la droite qui passe par \(0\) et \(x\) et que c’est l’ensemble \(\mathbf{R}x=\{\lambda x, \lambda\in\mathbf{R}\}\).

Remarque. Si \(v\in\mathbf{R}^3\) est un vecteur non nul, \(\lambda\in\mathbf{R}\setminus\{0\}\) et \(w=\lambda v\) alors \(p(v)=p(w)\). En effet, \(v\) et \(w\) appartiennent à la même droite vectorielle.

Définition 2.3 Soit \(p_1,p_2,p_3\in \mathbf{P}_2\). On dit que \(p_1,p_2\) et \(p_3\) sont alignés s’il existe \(P\) plan vectoriel de \(\mathbf{R}^3\) tel que \(p_1,p_2,p_3\in P\).

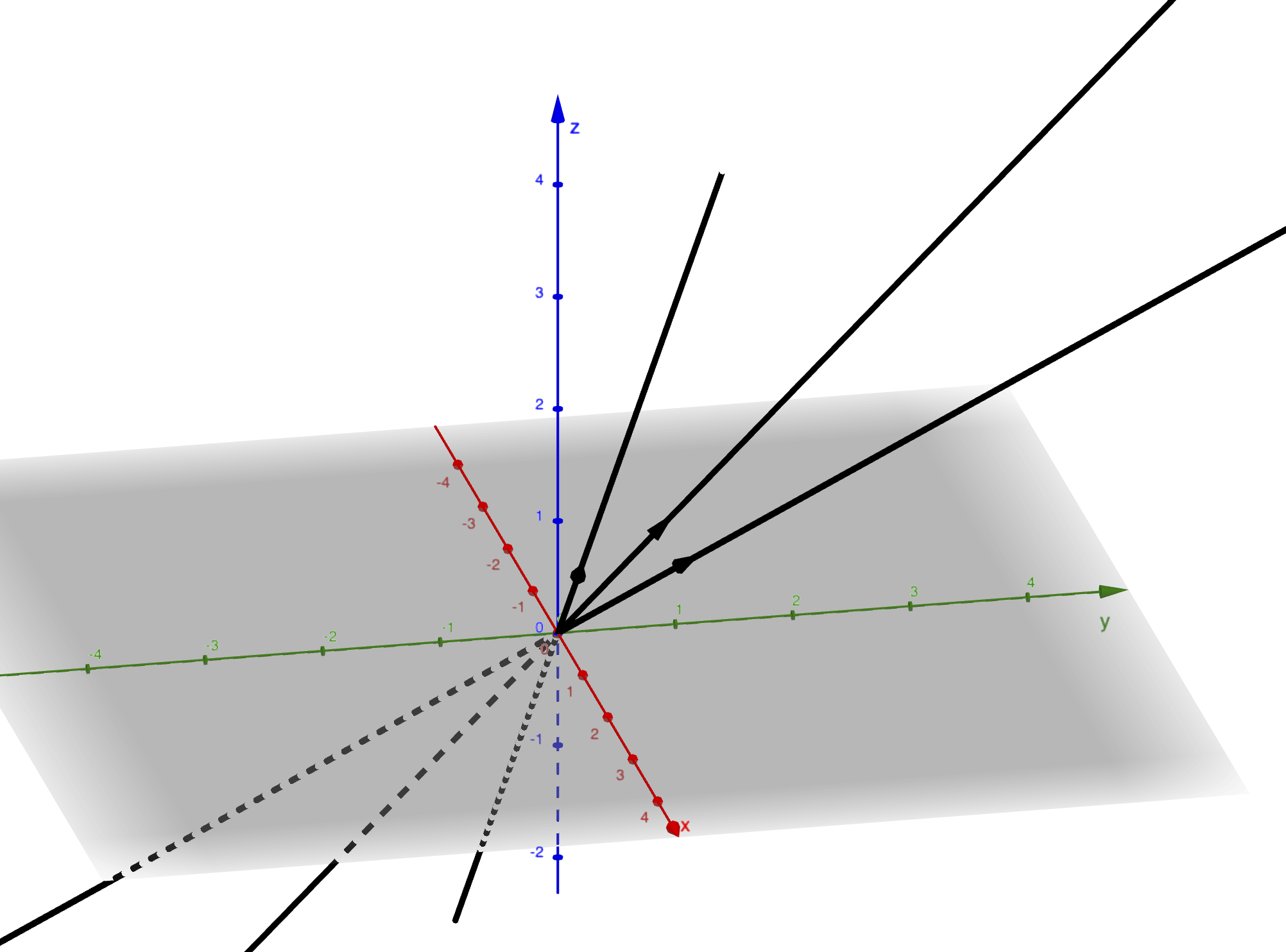
Figure 2.3: Trois points de l’espace projectif (trois droites) non alignés.

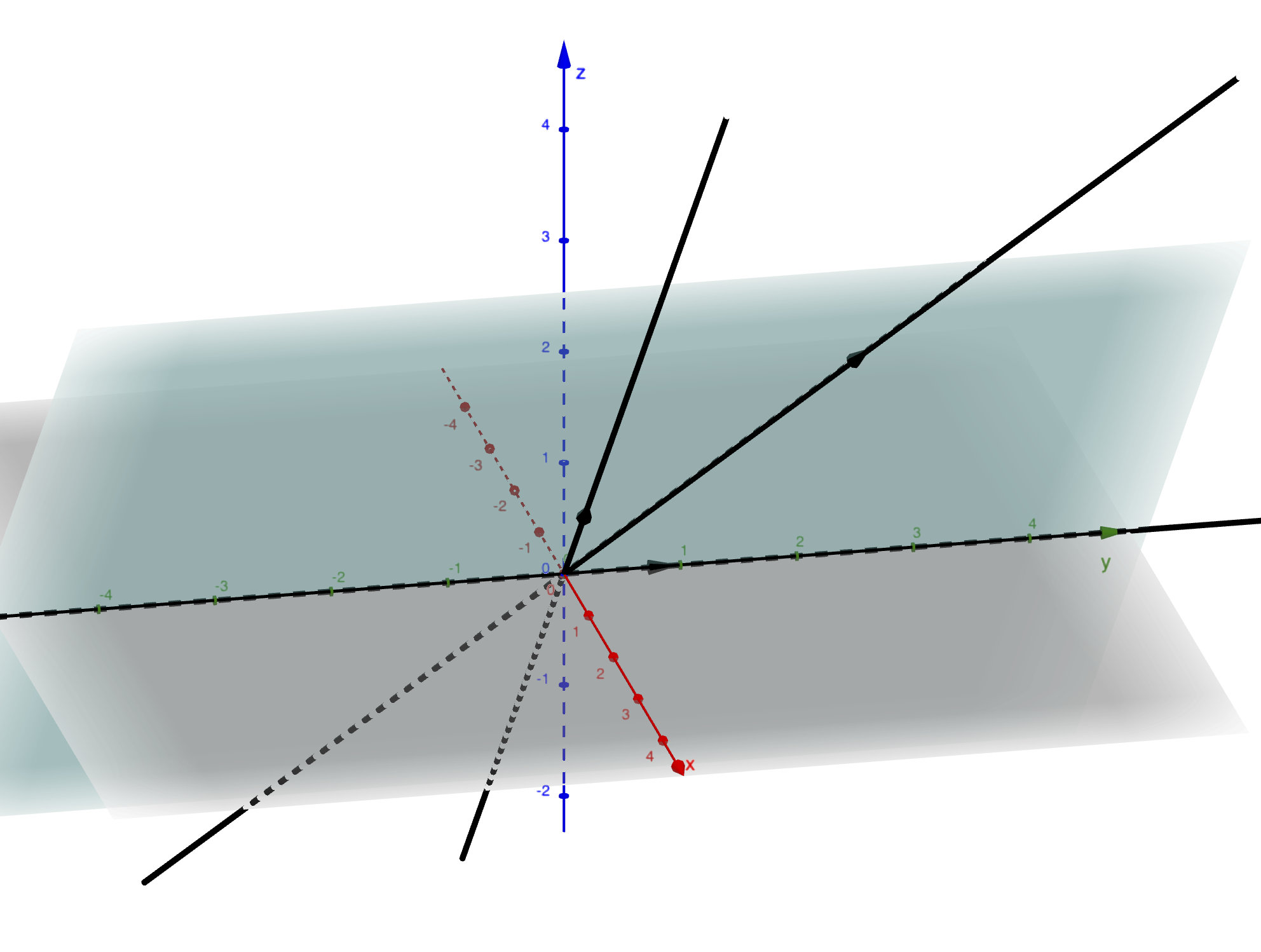
Figure 2.4: Trois points de l’espace projectif (trois droites) alignés.

Exemple 2.1 Les droites engendrées par les vecteurs \(e_1=(1,0,1)\), \(e_2=(0,1,1)\) et \(e_3=(1,1,1)\) ne sont pas alignées car ces trois vecteurs forment une base de \(\mathbf{R}^3\).

Les droites engendrées par les vecteurs \(v_1=(1,0,1)\) \(v_2=(0,1,0)\) et \(v_3=(3,2,3)\) sont alignées. Elles sont incluses dans le plan d’équation \(x=z\). On peut aussi voir que ces vecteurs sont liés car \(v_3=3v_1+2v_2\).

Lemme 2.1 Si \(p_1=p(v_1)\), \(p_2=p(v_2)\) et \(p_3=p(v_3)\) alors les points \(p_1,p_2,p_3\in \mathbf{P}_2\) sont non alignés si et seulement si \((v_1,v_2,v_3)\) est une base de \(\mathbf{R}^3\).

Preuve. En effet, si trois vecteurs dans sont un même un plan vectoriel alors ils sont liés et donc ils ne forment pas une base. Réciproquement, s’ils forment une base, ils engendrent tout \(\mathbf{R}^3\) et ne peuvent donc être contenus dans un plan vectoriel.

2.3 Correspondance affine – projectif

On peut voir le plan \(\mathbf{R}^2\) comme une partie du plan projectif de la manière suivante:

Définition 2.4 (Passage affine -> projectif) Soit \(p\) un point de \(\mathbf{R}^2\) de coordonnées \((x,y)\), on lui associe le point \(\overline{p}=p((x,y,1))\), c’est-à-dire que \(\overline{p}\) est la droite vectorielle de \(\mathbf{R}^3\) qui passe par le point \((x,y,1)\).

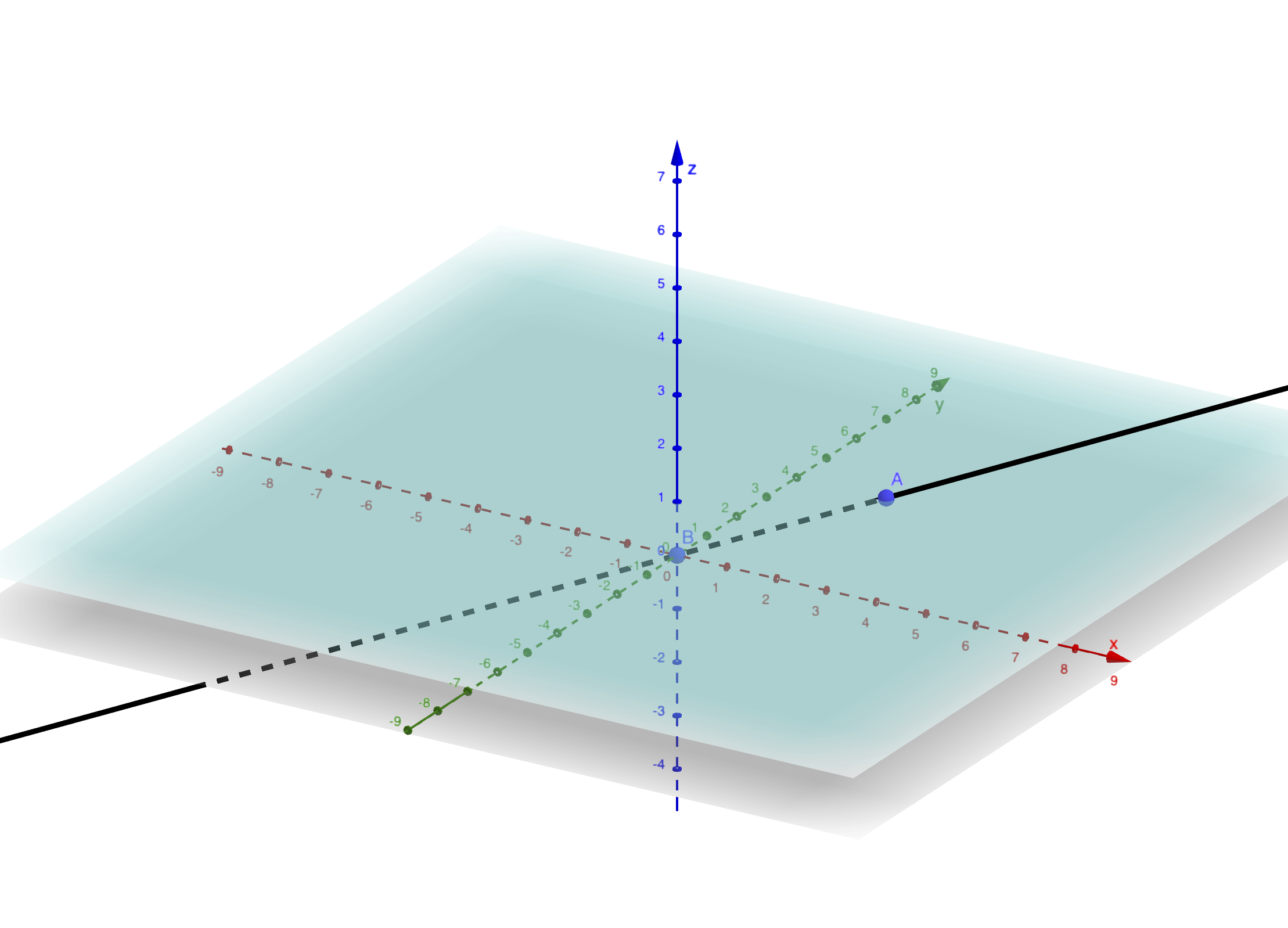
Figure 2.5: Le point A de coordonnées (x,y,1) et la droite qui passe par ce point.

Réciproquement, on a la construction inverse.

Définition 2.5 (Passage projectif -> affine) Soit \(\overline{p}\) un point de \(\mathbf{P}_2\) donné par \(\overline{p}=p(v)\) où \(v=(x,y,z)\in\mathbf{R}^3\) avec \(z\neq0\). On associe à \(\overline{p}\) le point \(p=(x/z,y/z)\in\mathbf{R}^2\).

Remarque. L’opération \(\overline{p}\mapsto p\) n’est pas définie pour tous les points \(\overline{p}\) de \(\mathbf{P}_2\), en effet, la division par 0, si \(z=0\), empêche de définir \(p\) lorsque \(z=0\). De tels points avec \(z=0\) sont dit à l’infini.

Les opérations \(p\mapsto \overline{p}\) et \(\overline{p}\mapsto p\) sont inverses l’une de l’autre et souvent on aura tendance à ne pas distinguer \(p\) de \(\overline{p}\).

Remarque. On parle de plan affine pour \(\mathbf{R}^2\) lorsqu’on considère des droites affines, c’est-à-dire des droites qui ne passent pas nécessairement par l’origine. Si on ne considère que des droites vectorielles (c’est-à-dire passant par l’origine 0), on parle d’espace vectoriel. Par exemple, dans ce chapitre, on ne parle que de l’espace vectoriel \(\mathbf{R}^3\).

Géométriquement ou visuellement, ce passage projectif-affine, se passe de la manière suivante. Si on part d’un point \((x,y)\) de \(\mathbf{R}^2\), on lui associe la droite vecotrielle qui passe par le point \((x,y,1)\) de \(\mathbf{R}^3\). Réciproquement, si on part d’une droite de \(\mathbf{R}^3\) qui rencontre le plan d’équation \(z=1\), on lui associe les deux premières coordonnées \((x,y)\) du point d’intersection de la droite avec le plan d’équation \(z=1\). Par exemple, si on considère la droite qui passe par le point de coordonnées \((x,y,z)\) avec \(z\neq0\), l’intersection avec le plan d’équation \(z=1\) est \((x/z,y/z,1)\). En effet, un point de la droite est de la forme \((\lambda x,\lambda y, \lambda z)\) avec \(\lambda\in\mathbf{R}\). Pour avoir \(\lambda z=1\), on a nécessairement \(\lambda=1/z\) d’où les coordonnées \((x/z,y/z,1)\).

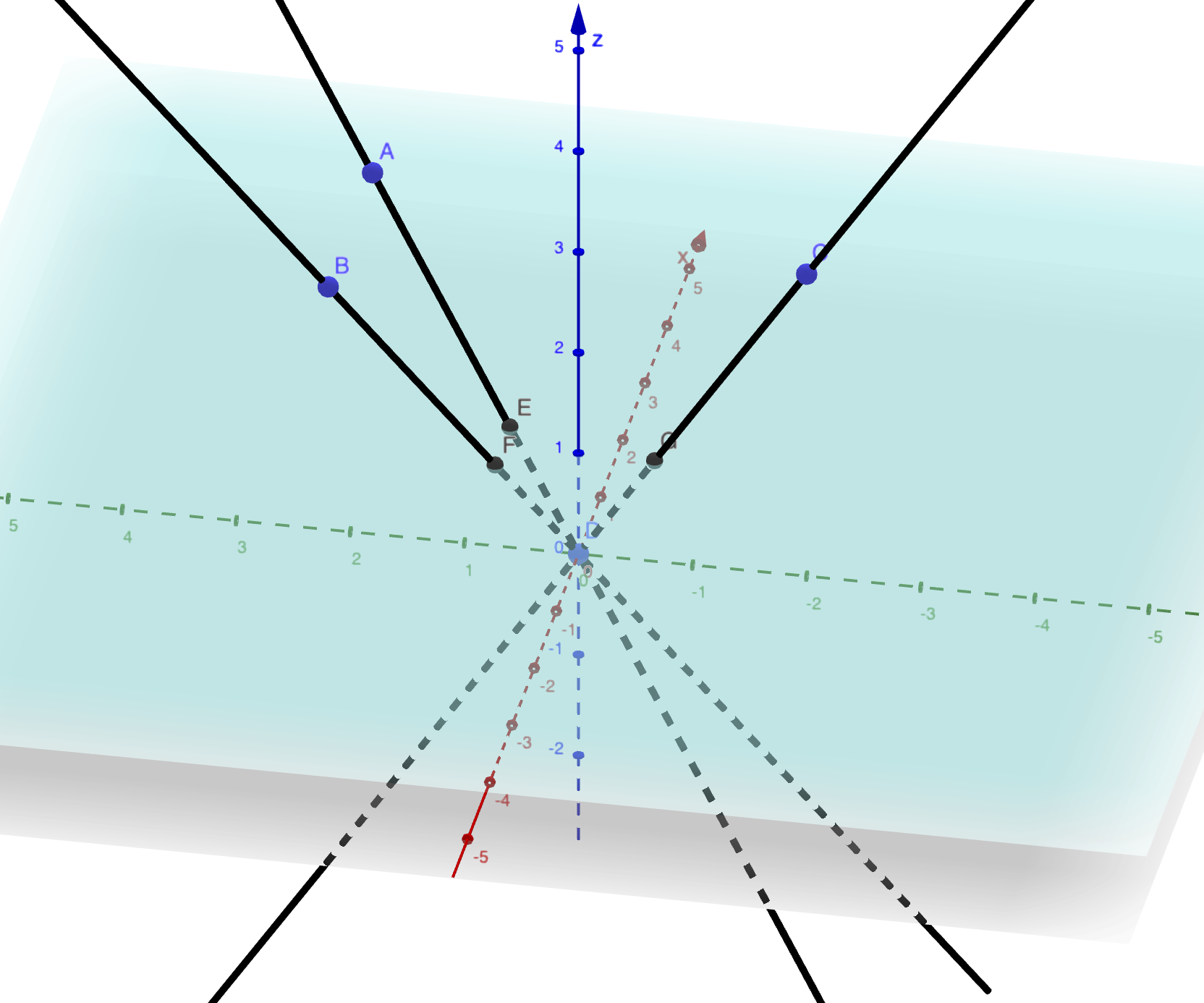
Figure 2.6: Passage de l’affine au projectif

Définition 2.6 Soit \(p_1,p_2,p_3\) trois points de l’espace \(\mathbf{R}^2\). On dit que ces points sont alignés s’il existe une droite affine qui passent par ces trois points.

Remarque. Dire que \(p_1,p_2,p_3\) sont alignés est équivalent à dire que les vecteurs \(\overrightarrow{p_1p_2}\) et \(\overrightarrow{p_1p_3}\) sont liés.

De plus si \((x_i,y_i)\), pour \(i=1,2,3\), sont les coordonnées de ces points alors dire qu’ils sont alignés signifie qu’il existe \(a,b,c,\in\mathbf{R}\) tels que les \((x_i,y_i)\) sont solutions de l’équation \(ax+by+c=0\) (qui est l’équation d’une droite affine).

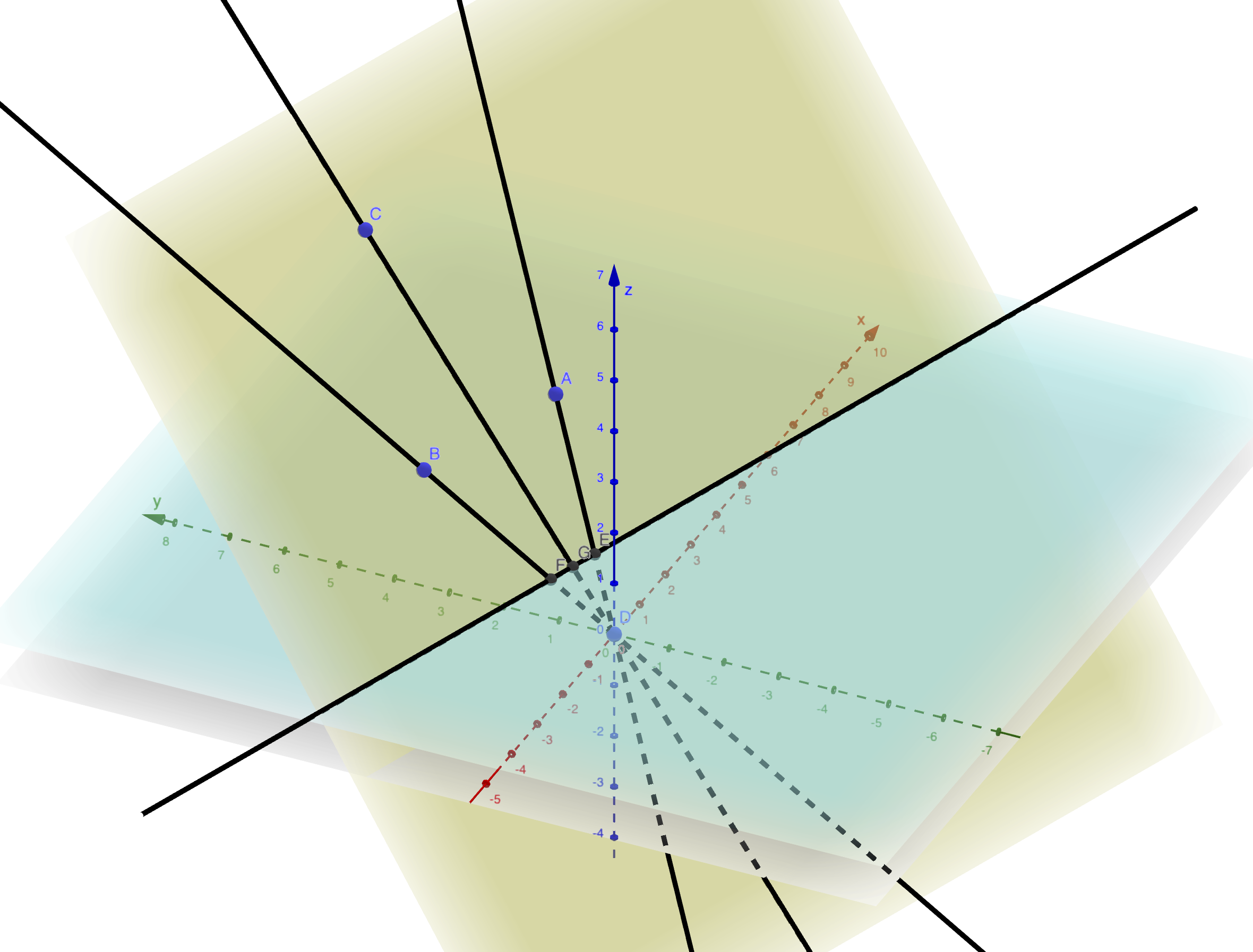
Figure 2.7: Points projectifs alignés

On image un oeil placé en \((0,0,0)\) qui regarde dans la direction de l’axe des \(z\). On considère trois points avec les coordonnées suivantes : \((-1,1.73,2)\), \((-1.5,-2.6,3)\) et \((4,0,4)\). C’est comme s’il voyait les points \((-1/2,\sqrt{3}/2,1)\), \((-1/2,-\sqrt{3}/2,1)\) et \((1,0,1)\) qui sont les trois sommets d’un triangle équilatéral dans le plan d’équation \(z=1\).

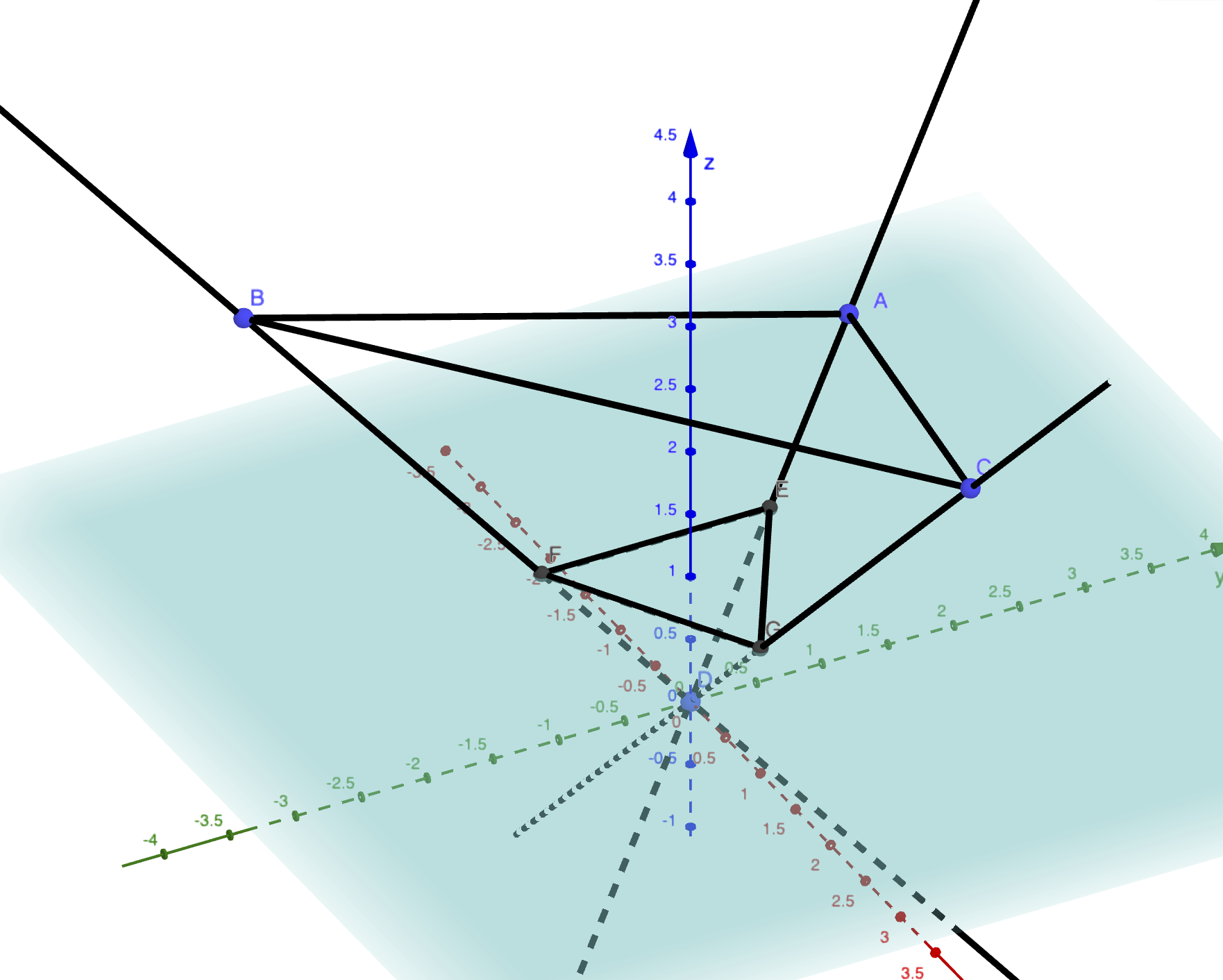
Figure 2.8: L’oeil placé en l’origine a l’impression que les point

Ce phénomène est exploité pour créer des illusions d’optique.

Figure 2.9: L’artiste Katy Ann Gilmore réalise une illusion d’optique à l’aide de perspective.

Proposition 2.1 Soit \((p_1,p_2,p_3)\) trois points de l’espace \(\mathbf{R}^2\) et \((\overline{p}_1,\overline{p}_2,\overline{p}_3)\) les trois points de l’espace projectif associés. Alors \(p_1,p_2,p_3\) sont alignés dans \(\mathbf{R}_2\) si et seulement si \(\overline{p}_1,\overline{p}_2, \overline{p}_3\) sont alignés dans \(\mathbf{P}_2\).

2.4 Transformations projectives

Rappelons qu’une application linéaire \(f\colon\mathbf{R}^3\to\mathbf{R}^3\) est inversible si \(f\) est bijective. Dans ce cas, son inverse \(f^{-1}\) est aussi une application linéaire. Matriciellement, si \(A\) est la matrice de \(f\) dans une certaine base alors \(f\) est inversible si \(A\) est inversible (\(\det(A)\neq0\)) et la matrice de \(f^{-1}\) est \(A^{-1}\).

Définition 2.7 Soit \(f\) une application linéaire inversible de \(\mathbf{R}^3\). On note \(\overline{f}\) l’application \(\mathbf{P}^2\to\mathbf{P}^2\) telle que

\[\overline{f}(p(v))=p(f(v)).\]

La définition signifie que l’image par \(\overline{f}\) de la droite engendrée par \(v\) et la droite engendrée par \(f(v)\).

La principale propriété des transformations projectives est de préserver l’alignement.

Proposition 2.2 Soit \(\overline{f}\) l’application projective \(\mathbf{P}_2\to\mathbf{P}_2\) associée à une application linéaire inversible \(f\colon\mathbf{R}^3\to\mathbf{R}^3\) alors pour trois points \(p_1,p_2,p_3\in\mathbf{P}_2\),

\(p_1,p_2,p_3\) sont alignés si et seulement si \(,\overline{f}(p_1),\overline{f}(p_2),\overline{f}(p_3)\) sont alignés.

Preuve. On choisit trois vecteurs \(v_1,v_2,v_3\in\mathbf{R}^3\) tels que \(p(v_i)=p_i\). Les \(p_i\) sont non alignés si et seulement si les vecteurs \(v_1,v_2,v_3\) forment une base de \(\mathbf{R}^3\). Maintenant, comme \(f\) est inversible, \((v_1,v_2,v_3)\) est une base si et seulement si \((f(v_1),f(v_2),f(v_3))\) est une base, c’est-à-dire si et seulement si les points \(p_1,p_2, p_3\) sont non alignés.

Remarque. On peut montrer qu’une bijection de \(\mathbf{P}_2\) qui préservent l’alignement est nécessairement une transformation projective. C’est le théorème fondamental de la géométrie projective.

2.5 Repères projectifs

Définition 2.8 (Repère projectif) Un repère projectif est un quadruplet \((p_1,p_2,p_3,p_4)\) de points de \(\mathbf{P}_2\) qui sont trois à trois non alignés.

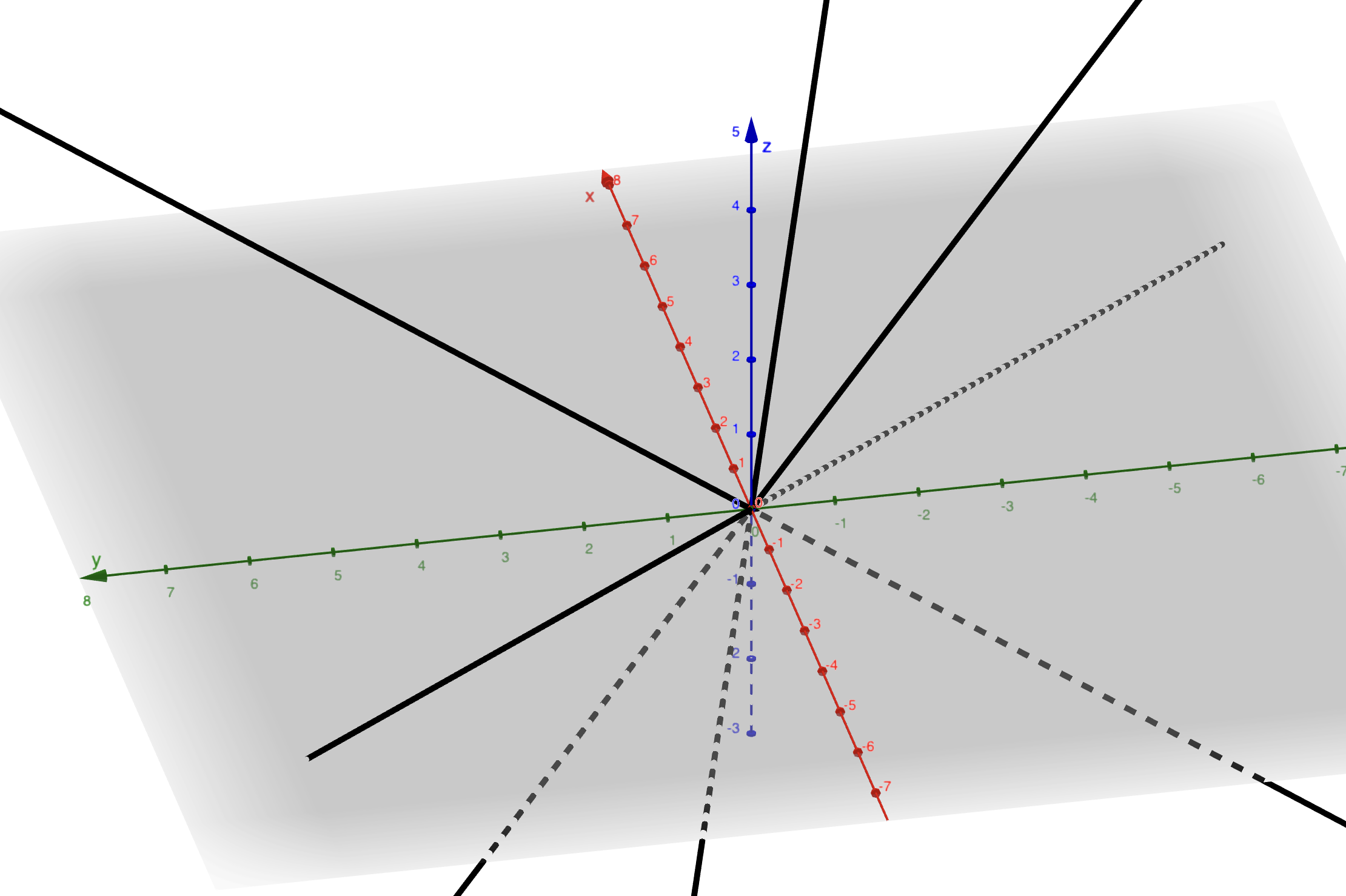
Figure 2.10: Les 4 droites noires non alignées 3 à 3 forment un repère projectif.

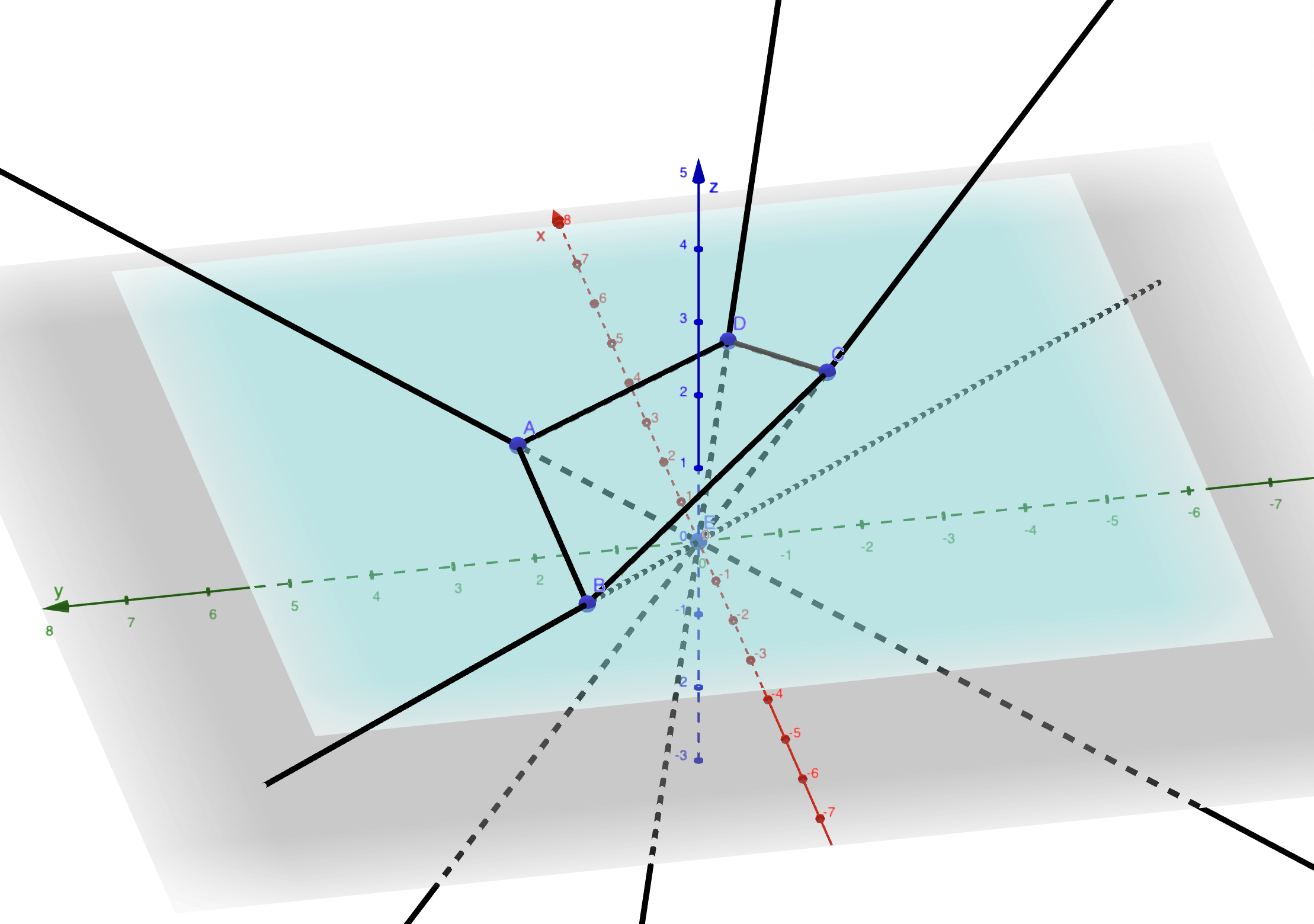
Figure 2.11: Le passage affine-projectif pour ce repère projectif.

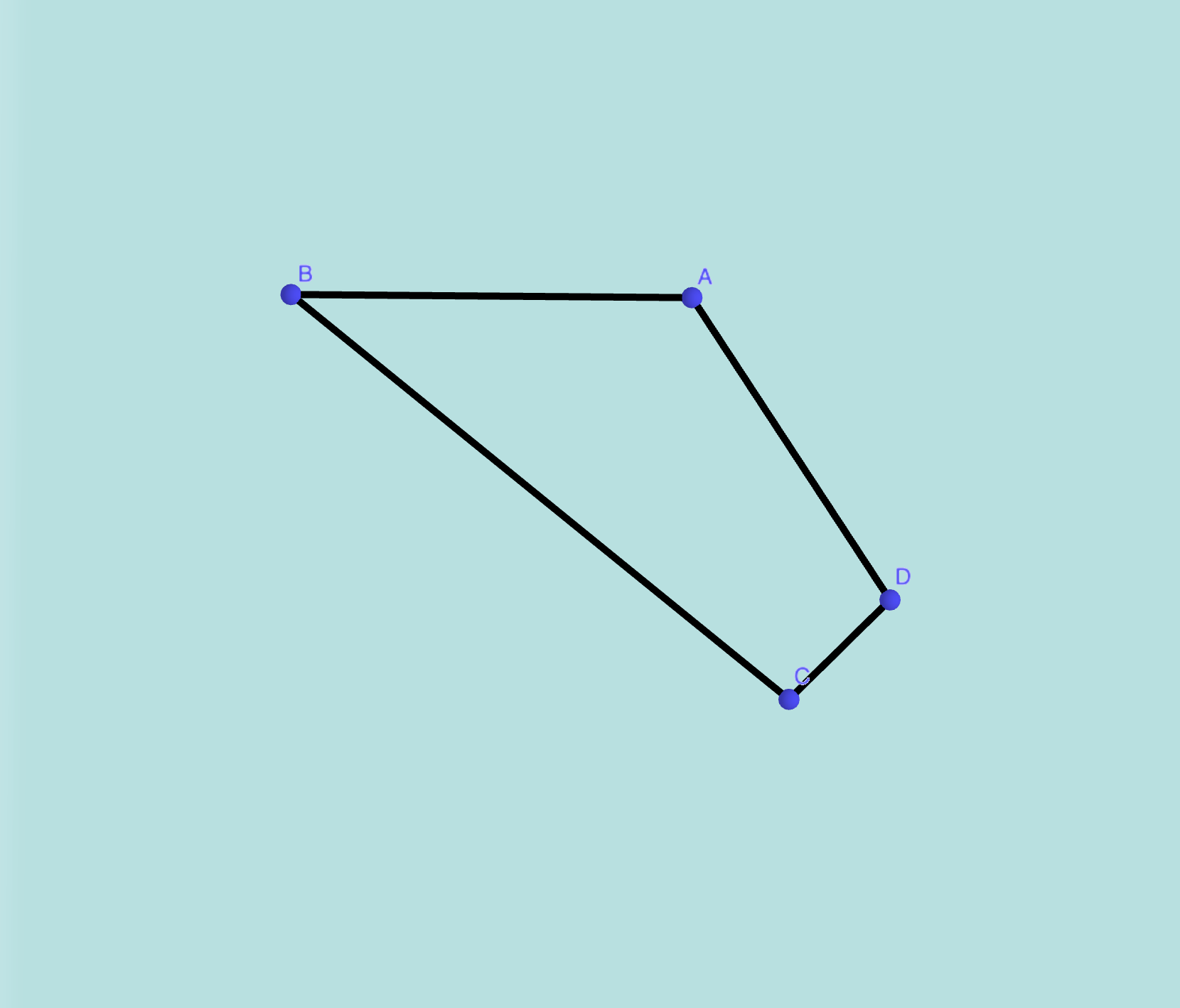
Figure 2.12: La version affine d’un repère projectif : 4 points non-alignés trois à trois.

Définition 2.9 Soit \((p_1,p_2,p_3,p_4)\) un repère projectif de \(\mathbf{P}_2\). Une base adaptée à ce repère est une base \((v_1,v_2,v_3)\) de \(\mathbf{R}^3\) telle que \(p_1=p(v_1), p_2=p(v_2), p_3=p(v_3)\) et \(p(v_1+v_2+v_3)=p_4\).

Exemple 2.2 Si on prend \(v_1=(1,0,0)\), \(v_2=(0,1,0)\) et \(v_3=(0,0,1)\) et \(v_4=(1,1,1)\) et \(p_i=(v_i)\) pour \(i=1,\dots, 4\). Alors \((p_1,p_2,p_3,p_4)\) est un repère projectif de \(\mathbf{P}_2\) et \((v_1,v_2,v_3)\) est une base adaptée.

En fait dans la définition de base adaptée, le vecteur \(v_4\) a pour coordonnées \((1,1,1)\) dans la base \((v_1,v_2,v_3)\).

Proposition 2.3 Soit \((p_1,p_2,p_3,p_4)\) un repère projectif de \(\mathbf{P}_2\). Alors il existe \((v_1,v_2,v_3)\) base adaptée à ce repère.

Preuve. Les \(p_i\) sont des droites, on choisit un vecteur non nul \(v_i\) dans chacune de ces droites, c’est-à-dire tels que \(p(v_i)=p_i\).

Comme \(p_1,p_2,p_3\) sont non alignés, \((v_1,v_2,v_3)\) est une base de \(\mathbf{R}^3\). Ainsi, il existe des nombres réels \(\lambda_1,\lambda_2,\lambda_3\in\mathbf{R}\) tels que \(v_4=\lambda_1 v_1+\lambda_2 v_2+\lambda_3 v_3\). Ces nombres sont tous non nuls sinon si \(\lambda_1=0\) par exemple, \(v_4\in \mathrm{Vect}(v_2,v_3)\) et donc \((v_2,v_3,v_4)\) est liée, ce qui contredit le fait que \((p_2,p_3,p_4)\) sont non alignés.

Posons \(v'_1=\lambda_1 v_1, v'_2=\lambda_2v_2, v'_3=\lambda_3v_3\) et \(v'_4=v_4\). La famille \((v_1', v_2',v_3')\) est libre car si \(\lambda_1'v'_1+\lambda_2'v'_2+\lambda_3'v'_3=0\) alors \((\lambda'_1\lambda_1)v_1+(\lambda'_2\lambda_2)v_2+(\lambda'_3\lambda_3)v_3=0\) et comme \((v_1,v_2,v_3)\) est libre \(\lambda_i'\lambda_i=0\) pour \(i=1,2,3\). Finalement, comme \(\lambda_i\neq 0\), \(\lambda_i'=0\).

Comme nous sommes en dimension 3, \((v_1', v_2',v_3')\) est donc une base et on a \(v'_4=v_1'+v_2'+v_3'\). De plus, on a bien \(p(v_i')=p(v_i)=p_i\) pour \(i=1,\dots,4\) donc \((v_1,v_2,v_3)\) est une base adaptée à ce repère projectif.

Remarque. La preuve du théorème nous donne une méthode pour trouver une base adaptée à un repère donné. Si \((p_1,p_2,p_3,p_4)\) est un repère projectif avec des vecteurs \(v_i\) tels que \(p_i=p(v_i)\) alors on cherche \(x,y,z\in\mathbf{R}\) tels que \(v_4=xv_1+yv_2+zv_3\) (ce sont les coordonnées de \(v_4\) dans la base \((v_1,v_2,v_3)\)). On résoud ce système et on prend \(v'_1=xv_1\), \(v_2'=yv_2\), \(v_3'=zv_3\) et \(v'_4=v_4\) alors \((v'_1,v'_2,v'_3)\) est une base adaptée à ce repère.

Exemple 2.3 On se donne les vecteurs \(v_1=(1,0,0)\), \(v_2=(0,1,0), v_3=(0,0,1)\) et \(v_4=(1,2,3)\) et \(p_i=p(v_i)\) pour \(i=1,2,3,4\). Comme \(v_4=1v_1+2v_2+3v_3\), une base adaptée au repère \((p_1,p_2,p_3,p_4)\) est \((v_1,2v_2,3v_3)\).

Théorème 2.1 Soit \((p_1,p_2,p_3,p_4)\) et \((p'_1,p'_2,p'_3,p'_4)\) deux repères projectifs. Il existe une transformation projective \(\overline{f}\) telle que \(\overline{f}(p_i)=p'_i\) pour tout \(i=1,\dots,4\).

Preuve. Grâce à la Proposition 2.3, il existe des bases adaptées \((v_1,v_2,v_3)\) et \((v'_1,v'_2,v'_3)\) aux repères projectifs \((p_1,p_2,p_3,p_4)\) et \((p'_1,p'_2,p'_3,p'_4)\). Posons \(v_4=v_1+v_2+v_3\) et \(v'_4=v'_1+v'_2+v'_3\). On a donc \(p(v_4)=p_4\) et \(p(v_4')=p'_4\).

On définit une application linéaire \(f\colon\mathbf{R}^3\to\mathbf{R}^3\) par \(f(v_i)=v_i'\), c’est-à-dire que si \(v\) est un vecteur de coordonnées \((x,y,z)\) dans la base \((v_1,v_2,v_3)\) (\(v=xv_1+yv_2+zv_3\)) alors \(f(v)=xv'_1+yv'_2+zv'_3\). En particulier \(f(v_4)=f(v_1+v_2+v_3)=f(v_1)+f(v_2)+f(v_3)=v'_1+v'_2+v'_3=v'_4\).

Ainsi \(\overline{f}(p_i)=p(f(v_i))=p(v'_i)=p'_i\). Donc l’image du repère projectif \((p_1,p_2,p_3,p_4)\) par \(\overline{f}\) est \((p'_1,p'_2,p'_3,p'_4)\).

Ce théorème se traduit de la manière suivante pour les transformations du plan \(\mathbf{R}^2\). Rappelons qu’une application \(g\colon \mathbf{R}^2\to\mathbf{R}^2\) préserve l’alignement si \(g(p_1),g(p_2),g(p_3)\) sont alignés dès que \(p_1,p_2,p_3\) sont alignés.

Théorème 2.2 Soit \((p_1,p_2,p_3,p_4)\) et \((p'_1,p'_2,p'_3,p'_4)\) deux quadruplets de points de \(\mathbf{R}^2\) vérifiant chacun que trois à trois les points ne sont pas alignés. Alors il existe une transformation \(g\colon \mathbf{R}^2\to\mathbf{R}^2\) qui préserve l’alignement telle que \(g(p_i)=p'_i\) pour \(i=1,\dots,4\).

Preuve. Soit \((x_i,y_i)\) les coordonnées du point \(p_i\) dans \(\mathbf{R}^2\) et \((x_i',y_i')\) celles des points \(p_i'\). On considère alors les vecteurs \(v_i=(x_i,y_i,1)\) et \(v'_i=(x'_i,y'_i,1)\). On définit \(\overline{p_i}=p(v_i)\) et \(\overline{p_i'}=p(v_i')\). Comme les \(p_i\) et les \(p_i'\) sont trois à trois non alignés, il en est de même pour les \(\overline{p_i}\) et les \(\overline{p_i'}\). Ainsi, \((\overline{p_1},\dots,\overline{p_4})\) et \((\overline{p_1'},\dots,\overline{p_4'})\) sont des repères projectifs et on peut leur appliquer le théorème 2.1. Ainsi, il existe \(f\colon\mathbf{R}^3\to\mathbf{R}^3\) telle que la transformation projective \(\overline{f}\colon\mathbf{P}_2\to\mathbf{P}_2\) satisfait \(\overline{f}(p_i)=p_i'\). On définit alors \(g\colon\mathbf{R}^2\to\mathbf{R}^2\) de la manière suivante :

\[g(x,y)=(x'/z',y'/z')\]

où \((x',y',z')=f(x,y,z)\), c’est-à-dire que \((x'/z',y'/z',1)\) sont les coordonnées du point d’intersection de la droite engendrée par \(f(x,y,z)\) et le plan d’équation \(z=1\).

Par construction, on a bien \(g(p_i)=p_i'\) et \(g\) préserve l’alignement.

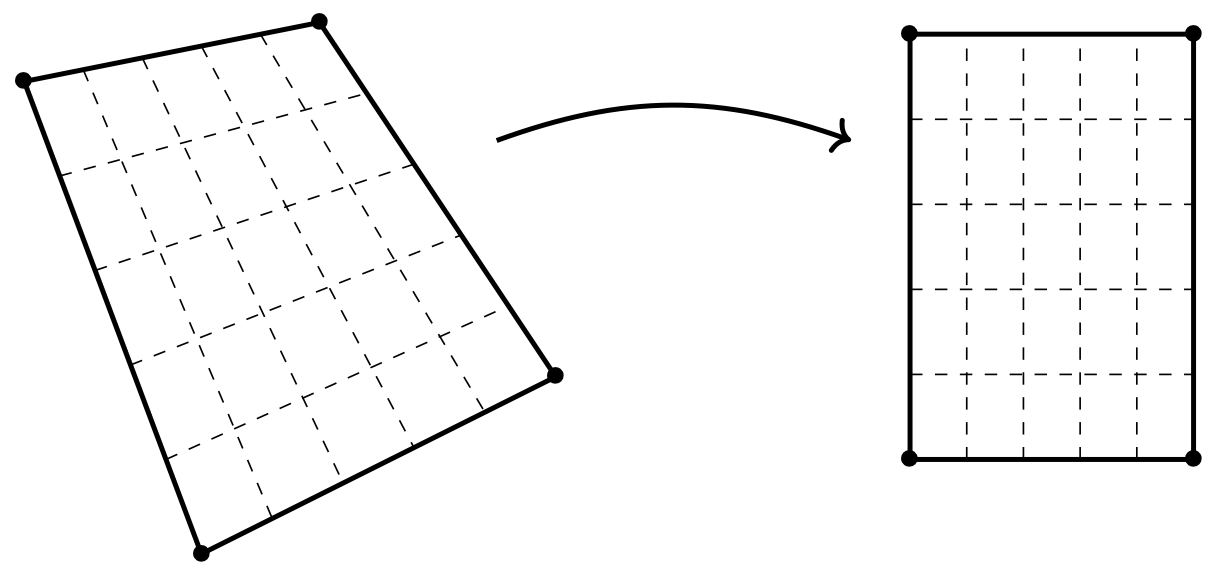
Figure 2.13: Deux repères projectifs et une application projective qui envoie l’un sur l’autre.

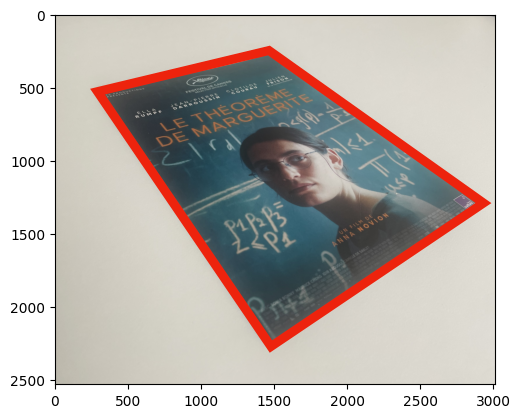
Figure 2.14: Les quatres du poster sur la table forment un repère projectif, on peut les envoyer sur les sommets d’un rectangle au format A4 à l’aide d’une transformation projective

2.6 Mise en pratique du changement de perspective

On suppose que l’on a deux quadruplets de points \((p_1,p_2,p_3,p_4)\) et \((p'_1,p'_2,p'_3,p'_4)\) dans \(\mathbf{R}^2\) avec des coordonnées \((x_i,y_i)\) et \((x_i',y_i')\). Comment mettre en pratiquement expliquement le changement de repère projectifs \((p_1,p_2,p_3,p_4)\) à \((p'_1,p'_2,p'_3,p'_4)\) et pouvoir l’appliquer à n’importe quel point \((x,y)\in\mathbf{R}^2\) ? Voici les étapes.

1. On commence par calculer des bases adaptées aux repères projectifs. On pose \[A=\begin{bmatrix}x_1&x_2&x_3\\ y_1& y_2 &y_3\\1&1&1\end{bmatrix}\] et \[A'=\begin{bmatrix}x'_1&x'_2&x'_3\\ y'_1& y'_2 &y'_3\\1&1&1\end{bmatrix}\]
2. On calcule les inverses \(B=A^{-1}\) et \(B'=(A')^{-1}\) de ces matrices.
3. On obtient les coordonnées \((\lambda_1,\lambda_2,\lambda_3)\in\mathbf{R}^3\) de \(\begin{bmatrix}x_4\\y_4\\1\end{bmatrix}\) dans la base \((v_1,v_2,v_4)\) avec

\[\begin{bmatrix}\lambda_1\\ \lambda_2\\ \lambda_3\end{bmatrix}=B\begin{bmatrix}x_4\\y_4\\1\end{bmatrix}.\] 4. On pose alors \[C=\begin{bmatrix}x_1&x_2&x_3\\ y_1& y_2 &y_3\\1&1&1\end{bmatrix}\begin{bmatrix}\lambda_1&0&0\\0&\lambda_2&0\\0&0&\lambda_3\end{bmatrix}=\begin{bmatrix}\lambda_1x_1&\lambda_2x_2&\lambda_3x_3\\ \lambda_1y_1&\lambda_2 y_2 &\lambda_3y_3\\\lambda_1&\lambda_2&\lambda_3\end{bmatrix}\] 5.On calcul de même les coordonnées \((\lambda'_1,\lambda'_2,\lambda'_3)\in\mathbf{R}^3\) de \(\begin{bmatrix}x'_4\\y'_4\\1\end{bmatrix}\) dans la base \((v'_1,v'_2,v'_4)\) avec

\[\begin{bmatrix}\lambda'_1\\ \lambda'_2\\ \lambda'_3\end{bmatrix}=B'\begin{bmatrix}x'_4\\y'_4\\1\end{bmatrix}.\] 6. Et on calcule \[C'=\begin{bmatrix}x'_1&x'_2&x'_3\\ y'_1& y'_2 &y'_3\\1&1&1\end{bmatrix}\begin{bmatrix}\lambda'_1&0&0\\0&\lambda'_2&0\\0&0&\lambda'_3\end{bmatrix}=\begin{bmatrix}\lambda'_1x'_1&\lambda'_2x'_2&\lambda'_3x'_3\\ \lambda'_1y'_1&\lambda'_2 y'_2 &\lambda'_3y'_3\\\lambda'_1&\lambda'_2&\lambda'_3\end{bmatrix}.\] 7. On pose \(P=C'C^{-1}\). On peut calculer facilement \(C^{-1}\) avec la formule \[C^{-1}=\begin{bmatrix}1/\lambda_1&0&0\\0&1/\lambda_2&0\\0&0&1/\lambda_3\end{bmatrix}B.\] Le changement de repères est alors

\[g\colon(x,y)\mapsto(x'/z',y'/z')\]

où \[\begin{bmatrix}x'\\y'\\z'\end{bmatrix}=P\begin{bmatrix}x\\y\\1\end{bmatrix}.\]

2.7 Exercices

Exercice 2.1 On considère les points \(u_1=(1,2,3)\), \(u_2=(1,1,1)\), \(u_3=(1.5,3,4.5)\) et \(u_4=(3,2,4)\). On pose \(p_i=p(u_i)\in\mathbf{P}_2\).

Quels sont les \(i\) et \(j\) tels que \(p_i=p_j\) ?

Exercice 2.2 On considère les points \((2,0,2)\), \((0,\sqrt{2},\sqrt{2})\), \((3,3,3)\) et \((0,0,1.5)\). Un observateur se place en \((0,0,0)\) et regarde dans la direction de l’axe des \(z\).

1. Quelle figure voit-il ?
2. Représenter la situation avec Geogebra.

Exercice 2.3 On considère les vecteurs \(v_1=(1,2,3)\), \(v_2=(0,1,2)\) et \(v_3=(2,2,3)\) et \(u_1=(1,0,2)\), \(u_2=(0,2,3)\) et \(u_3=(2,2,7)\) de \(\mathbf{R}^3\). On pose \(p_i=p(v_i)\) et \(q_i=p(u_i)\in\mathbf{P}_2\) pour \(i=1,2,3\).

1. Les points \(p_1,p_2,p_3\) sont-ils alignés ?
2. Les points \(q_1,q_2,q_3\) sont-ils alignés ?

Exercice 2.4 Démontrer la Proposition 2.1.

Exercice 2.5 On pose \(v_1=(1,0,0)\), \(v_2=(1,1,0)\), \(v_3=(1,1,1)\) et \(v_4=(3,2,1)\) et on pose \(p_i=p(v_i)\).

1. Montrer que \((p_1,p_2,p_3,p_4)\) est un repère projectif.
2. Montrer que \((v_1,v_2,v_3)\) est une base adaptée à ce repère

Exercice 2.6 On pose \(v_1=(0,1,1)\), \(v_2=(1,0,1)\), \(v_3=(1,1,0)\) et \(v_4=(1,0,0)\) et \(p_i=p(v_i)\).

1. Montrer que \((p_1,p_2,p_3,p_4)\) est un repère projectif.
2. Trouver une base adaptée à ce repère projectif.

Exercice 2.7 On considère les points \(p_1=(0,0),p_2=(1,0),p_3=(0,1)\) et \(p_4=(1,1)\) dans \(\mathbf{R}^2\) et les points \(p'_1=(0,0), p'_2=(3,1), p'_3=(2,1)\) et \(p'_4=(5,3/2)\).

On souhaite mettre en place le changement de perspective de \((p_1,p_2,p_3,p_4)\) à \((p'_1,p'_2,p'_3,p'_4)\) comme dans la section “Mise en pratique du changement de perspective”.

1. Donner les matrices \(A\) et \(A'\).
2. Calculer les matrices \(B\) et \(B'\).
3. Calculer les coefficients \((\lambda_1,\lambda_2,\lambda_3)\) et les coefficients \((\lambda'_1,\lambda'_2,\lambda'_3)\).
4. En déduire les matrices \(C\) et \(C'\).
5. Calculer la matrice \(P\).
6. Donner l’expression du changement de perspective \(g\).
7. Vérifier que \(g(p_i)=p'_i\) pour \(i=1,\dots,4\).
8. Calculer l’image de \((1/2,1/2)\) par \(g\).
9. Bonus : Avec Geogebra donner l’image des droites d’équation \(y=1/5\), \(y=2/5\) \(y=3/5\) et \(y=4/5\) puis \(x=1/5\), \(x=2/5\), \(x=3/5\), \(x=4/5\) et représenter toute la situation.