
Objectif
Réduire la dimension des données,
en conservant le plus d'information possible.
...
Données
En lignes : $n$ "individus"
En colonnes : $m$ "variables" numériques
| Temps de réaction | Distance de freinage | |
|---|---|---|
| Conducteur 1 | 1.3s | 40m |
| Conducteur 2 | 1.8s | 70m |
| Conducteur 3 | 2s | 50m |
| ... | ... | ... |
Format d'un jeu de données
Première ligne = en-tête, "header"
Name, 100m, Long.jump, ...
Lignes suivantes : individus
Sebrle, 11.04, 7.58, ... Clay, 10.76, 7.4, ...
En R :
data = read.csv("decathlon.csv")Prétraitement
Données toujours centrées.
Données "standardisées" si échelles différentes.
FactoMineR le fait par défaut.
$\Rightarrow$ Pas de calculs à faire.
Questions
Ressemblances / différences entre individus ?
Corrélations entre variables ?
Objectif de l'ACP
Résumer les variables par un petit nombre de "variables synthétiques"
Intuition

Méthode
- Recherche d'un axe $v_1$ minimisant $I(v_1)$
- Recherche d'un axe $v_2$ minimisant $I(v_2)$
- ...
Sous contrainte : $v_i$ orthogonal à $v_1, \dots, v_{i-1}$.
$I(v_i)$ = somme des carrés des distances à l'axe (projeté orthogonal).
Méthode équivalente
- Recherche d'un axe $v_1$ maximisant $I(v_1)$
- Recherche d'un axe $v_2$ maximisant $I(v_2)$
- ...
Sous contrainte : $v_i$ orthogonal à $v_1, \dots, v_{i-1}$.
$I(v_i)$ = "inertie projetée" = somme des carrés des distances (à 0) projetées sur l'axe.
Concernant les détails mathématiques (résumés), voir par exemple la section 3.1 de cet article.
Avec R
# Noms des variables
> names(data)
[1] "Name" "X100m" "Long.jump" "Shot.put" "High.jump"
[6] "X400m" "X110m.hurdle" "Discus" "Pole.vault" "Javeline"
[11] "X1500m" "Rank" "Points" "Competition"
# Chargement du package FactoMineR
# install.packages("FactoMineR")
> library(FactoMineR)
# Calcul de l'ACP
> res.pca = PCA(data[,-1], quanti.sup=11:12, quali.sup=13)Les colonnes 1, 12, 13 et 14 sont exclues : on ne regarde que les performances par discipline.
Visualisation
Individus projetés sur les premiers axes $v_1$, $v_2$.
Parfois aussi $v_3$ et $v_4$, voire au-delà.
# Affichage du nuage des individus, colorés
# selon leur performance au lancer de disque.
plot(res.pca, choix="ind", habillage=7)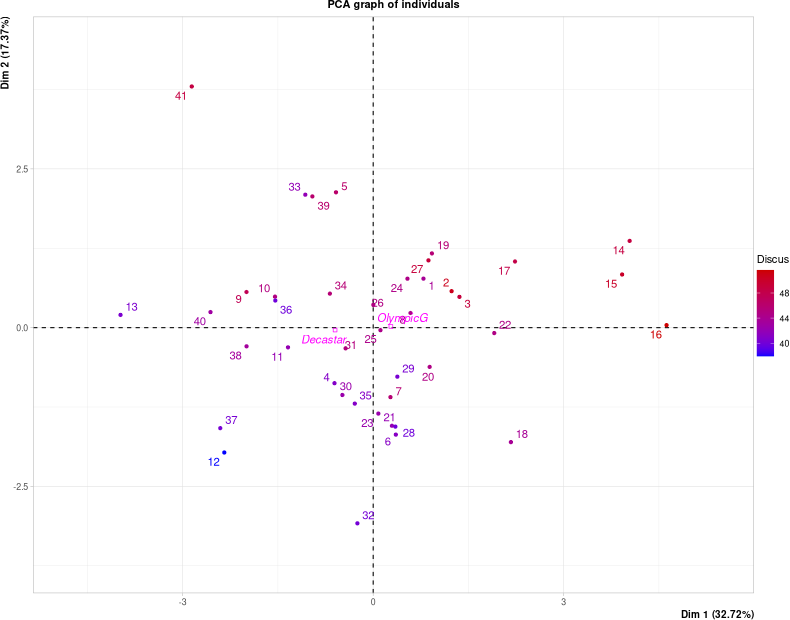
Qualité de représentation
res.pca$ind$cos2 # Limitation aux 10 individus les mieux représentés.
plot(res.pca, choix="ind", select="cos2 10")En général les individus extrêmes dans un plan donné sont les mieux représentés. En effet ce sont les points ayant le plus contribué à la construction des axes.
Variables synthétiques
On considère les coordonnées des individus sur les axes comme des variables :
# Vecteurs colonnes de dimension n :
> res.pca$ind$coord[1:3,]
Dim.1 Dim.2 Dim.3 Dim.4 Dim.5
1 0.7916277 0.7716112 0.8268412 1.1746274 0.7071590
2 1.2349906 0.5745781 2.1412470 -0.3548448 -1.9745714
3 1.3582149 0.4840209 1.9562580 -1.8565241 0.7952147
4 ... ... ... ... ...Le cosinus de l'angle formé par les variables initiales et ces variables synthétiques donne la corrélation.
Cercle des corrélations
Corrélations inter-variables.
Flèche proche du bord $\Rightarrow$ bonne représentation.
# Affichage du cercle des corrélations.
# On y voit aussi les variables supplémentaires.
> plot(res.pca, choix="var")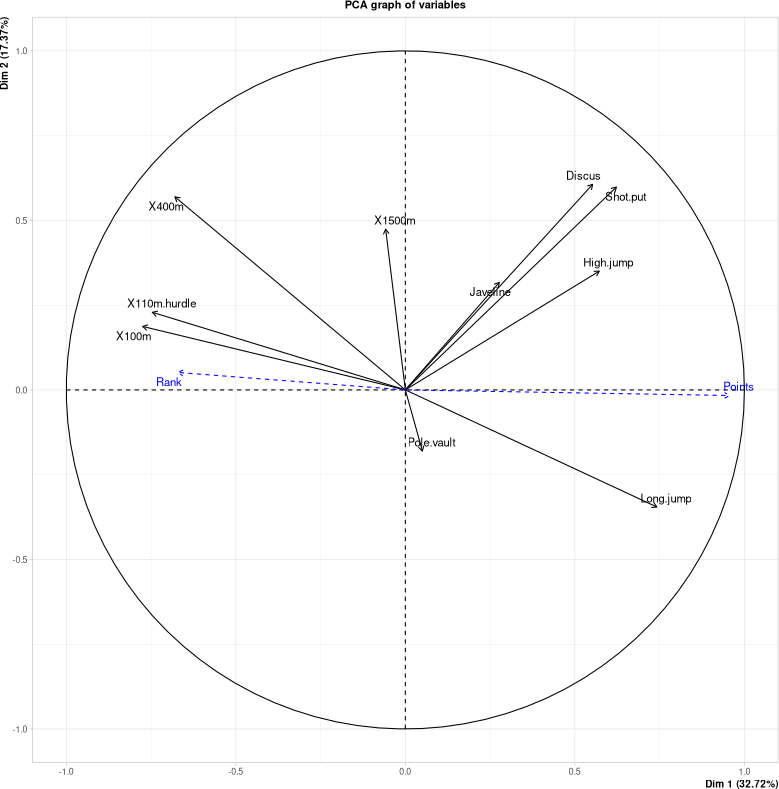
Vérification de l'interprétation
La visualisation aide mais ne suffit pas toujours.
> correlations = cor(data[,-c(1,12:14)]) ; correlations
X100m Long.jump Shot.put High.jump X400m
X100m 1.00000000 -0.59867767 -0.35648227 -0.24625292 0.520298155
Long.jump -0.59867767 1.00000000 0.18330436 0.29464444 -0.602062618
... ... ... ... ... ...
> library(corrplot) ; corrplot(correlations)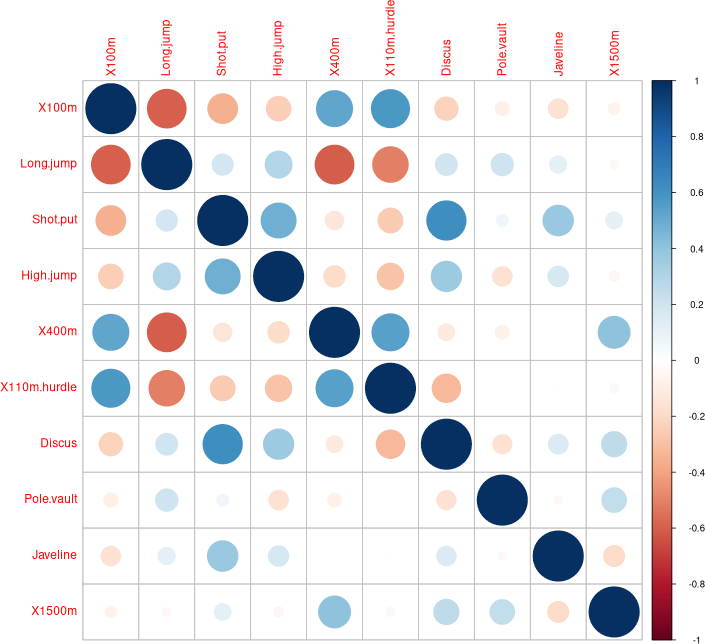
Individus extrêmes
Autre façon de vérifier l'interprétation : observer les caractéristiques des individus loin de l'origine.
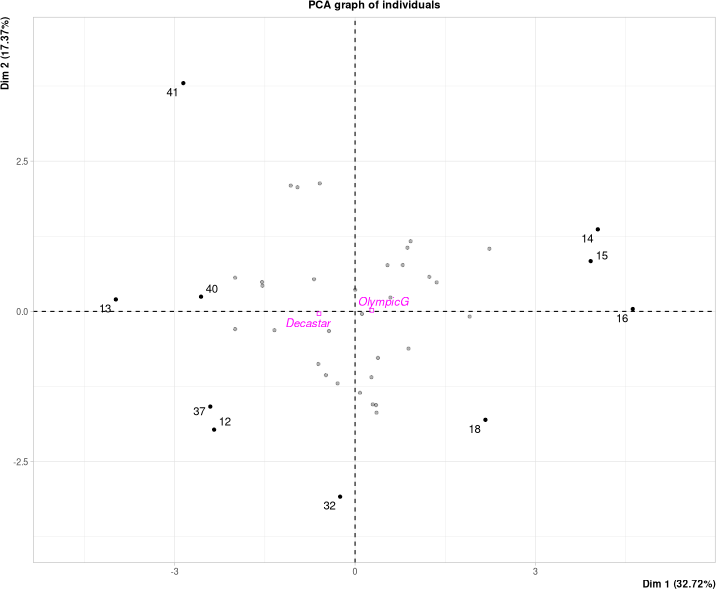
> data[c(13:16,40),
c("Name","Rank","Points")]
Name Rank Points
13 BOURGUIGNON 13 7313
14 Sebrle 1 8893
15 Clay 2 8820
16 Karpov 3 8725
40 Uldal 27 7495Combien d'axes retenir ?
# Pourcentage d'information cumulée :
> res.pca$eig[,3]
comp 1 comp 2 comp 3 comp 4 comp 5 comp 6 comp 7
32.71906 50.09037 64.13953 74.70804 81.55577 87.54846 ...Pour disposer de +85% de l'information totale,
il faut garder au moins 6 axes ici.
# Pour tracer dans le plan 3-4 :
plot(res.pca, axes=c(3, 4))
# Et pour avoir 6 axes :
res.pca = PCA(data, ncp=6, ...)Exercice 0
Lancez R, installez FactoMineR, puis chargez decathlon.csv
Regardez l'aide des fonctions : "?plot.PCA" par exemple.
Changez un peu les arguments,
observez $-$ et comprenez ! $-$ les effets.
Exercice 1
Récupérez le jeu de données "pizzas"
Effectuez une ACP et analysez le résultat.
Exercice 2
Récupérez le jeu de données "jeux vidéos"
Effectuez une ACP et analysez le résultat.
Suggestion de "corrigé"
Exercice 3.1
Cf. feuille exercices ACP.
Exercice 3.2
Téléchargez le jeu de données "covid".
- Conservez uniquement les lignes correspondant au 1er mars 2023.
- Que représentent les variables ?
- Certaines lignes semblent-elles ne pas correspondre à un pays ? Supprimez-les.
- Supprimez toutes les lignes comportant des valeurs manquantes. Qu'observez-vous ?
- Sélectionnez un nombre raisonnable de colonnes.
Exercice 3 - suite
- Effectuez une ACP sur le jeu de données réduit, sans valeurs manquantes. Alternative possible : utiliser le package missMDA
- Certains individus semblent-ils "extrêmes" ? (Très loin des autres sur le nuage). Expliquez en quoi ils sont uniques, puis relancez l'analyse sans eux.
- Certaines variables paraissent-elles très corrélées ? Vérifiez numériquement, expliquez, et, relancez l'analyse après suppression des redondances.
- Interprétez les graphes finalement obtenus. (Imaginez que vous êtes journaliste :) ).
Suggestion de "corrigé"
Pour aller plus loin
Allez voir le cours de François Husson à cette adresse. Écouter les vidéos est une bonne idée.
N'hésitez pas à faire les exercices aussi.