Thèmes de recherche
Sylvie Ruette

Mon domaine de recherche est la dynamique en temps discret. Un système dynamique topologique (X,T) est la donnée d'une transformation continue T de X dans X, l'espace X étant le plus souvent métrique compact. L'évolution du système est donnée par les itérations successives de la transformation, Tn désignant la transformation T composée n fois (Tn = T o T o ... o T ). On cherche à étudier le comportement du système pour des temps n tendant vers l'infini. La plupart de mes travaux concerne la dynamique en dimension 1 (transformations de l'intervalle ou de graphes topologiques) ; je m'intéresse également à la dynamique topologique abstraite, aux systèmes symboliques et aux rapports entre dynamique topologique et théorie ergodique.

Une des motivations pour étudier la dynamique en dimension 1, outre son intérêt propre, est d'essayer de comprendre certaines dynamiques en dimension supérieure. Dans un certain nombre de cas, on peut se ramener à étudier un système dynamique de dimension plus petite, notamment en considérant la section d'un flot ou l'action sur des fibres, ou en se restreignant à la partie « la plus intéressante » de la dynamique (par exemple, attracteur ou « squelette » représentant la dynamique).

Je présente ci-dessous un résumé de mes recherches, en présentant d'abord mes travaux récents. Les numéros entre crochets font référence à ma liste de publications.

Chaos Li-Yorke pour des transformations de graphes topologiques

Soit (X,T) un système dynamique topologique et d la distance sur X. Si x,y sont des points de X, (x,y) est un couple de Li-Yorke si

\begin{displaymath} \limsup_{n\to+\infty}d(T^n x, T^n y)>0\quad\mbox{et}\quad \liminf_{n\to+\infty}d(T^n x, T^n y)=0. \end{displaymath}

et un sous-ensemble S de X est brouillé si tout couple de points distincts dans S est un couple de Li-Yorke. Le système (X,T) est chaotique au sens de Li-Yorke s'il existe un ensemble brouillé non dénombrable. On sait que, si X est un intervalle compact ou un cercle, la présence d'un couple de Li-Yorke implique l'existence d'un ensemble de Cantor brouillé, et donc le chaos au sens de Li-Yorke. J'ai montré avec L'ubomír Snoha que le même résultat est valide pour les transformations de graphes topologiques [12] (un graphe topologique est obtenu en recollant un nombre fini de segments par certaines de leurs extrémités). Cette propriété n'est pas vraie en général : il existe des systèmes dynamiques symboliques admettant des couples de Li-Yorke mais dont le cardinal des ensembles brouillés est borné, ou dont les ensembles brouillés sont au plus dénombrables. Nous avons également montré que, quand X est dénombrable, un couple de Li-Yorke implique l'existence d'un ensemble brouillé infini.

Ensemble de rotation pour des transformations de graphes topologiques

Un graphe topologique est un espace compact connexe G dans lequel il existe un sous-ensemble fini E tel que chaque composante connexe de G\E est homéomorphe à un intervalle ouvert. Une boucle dans G est un sous-espace homéomorphe à un cercle. Les points périodiques occupent une place importante dans l'étude de la dynamique en dimension 1. Le théorème de Sharkovskii décrit les ensembles de périodes possibles pour une transformation de l'intervalle. Cette caractérisation des ensembles de périodes a été généralisée par étapes aux arbres, c'est-à-dire aux graphes topologiques sans boucle. Les transformations du cercle présentent un comportement différent : l'ensemble des périodes dépend du degré de la transformation et, dans le cas du degré 1, de l'intervalle de rotation. Ces résultats constituent la motivation de l'étude des points périodiques et de l'ensemble de rotation pour les graphes topologiques.

On considère un graphe topologique G ayant une unique boucle S et une transformation continue f de G dans G. Comme pour les transformations du cercle, on peut définir le degré de f et, si son degré est 1, le nombre de rotation d'un point. Pour cela, on considère T le revêtement universel de G (qui est un arbre infini), p la projection canonique de T dans G et F un relèvement continu de f (c'est-à-dire p o F = f o p), qui est une application de T dans T ; pour simplifier, on suppose dans la suite que T est inclus dans le plan complexe et que p-1(S) coïncide avec la droite réelle IR, pour que les opérations arithmétiques ci-dessous n'aient pas besoin d'être définies. Le degré de f, ou de F, est l'entier relatif d tel que, pour tout x dans T, F(x+1) = F(x) + d. Si F est de degré 1, on définit le nombre de rotation (quand il existe) d'un point x de T par

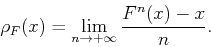
\begin{displaymath}\rho_F(x)=\lim_{n\to+\infty}\frac{F^n(x)-x}{n}. \end{displaymath}

On travaille au niveau du relèvement F. Les points périodiques de f correspondent aux points périodiques (mod 1) de F. On peut ensuite projeter les résultats afin de les exprimer pour f.

Signalons que le cas de degré d avec |d|>1 a été traité récemment par Alba Málaga et donne des résultats analogues au cas du cercle : l'ensemble des périodes contient tous les entiers si d>1 et tous les entiers sauf un nombre fini si d < -1.

Résultats généraux

Je collabore avec Lluís Alsedà depuis plusieurs années. Nous avons étudié l'ensemble des nombres de rotation d'une transformation F de T dans T continue de degré 1, où T est le revêtement universel d'un graphe contenant une unique boucle [9]. Nous avons montré que l'ensemble RotIR(F) des nombres de rotation des points de la droite réelle a des propriétés similaires à l'intervalle de rotation d'une transformation du cercle. En particulier, RotIR(F) est un intervalle compact non vide et, s'il est d'intérieur non vide, alors F a des points périodiques (mod 1) de période n pour tout entier n sauf un un nombre fini. De plus, si p/q est un rationnel dans l'intérieur de cet intervalle, alors il existe un point périodique (mod 1) appartenant à la droite réelle de nombre de rotation p/q et de période nq pour tout entier n assez grand, et si p/q est égal au minimum ou au maximum de cet intervalle, alors il existe un point périodique (mod 1) dans T de nombre de rotation p/q. La question des extrémités de l'intervalle RotIR(F), plus délicate, a nécessité l'introduction d'outils spécifiques. Quand p/q est égal au minimum ou au maximum de l'intervalle, on n'a pas d'information sur les périodes possibles du point périodique (qui dépendent de la topologie du graphe). Notons que ces résultats ont en fait été prouvés pour une classe d'espaces plus large que celle des graphes topologiques avec une unique boucle.

Nous avons également défini une famille de transformations F, appelées transformations peignées, dont l'ensemble de rotation a exactement les mêmes propriétés que celui d'une transformation du cercle de degré 1, notamment en ce qui concerne l'ensemble des périodes correspondant à un nombre de rotation donné et l'existence d'orbites bien ordonnées. Pour cela, nous utilisons la technique des « fonctions d'eau » introduite pour les transformations du cercle.

L'ensemble de rotation est-il fermé ?

L'intervalle RotIR(F) est un sous-ensemble de l'ensemble Rot(F), qui est l'ensemble des nombres de rotation de tous les points de T. En général, l'ensemble de rotation Rot(F) n'est pas nécessairement connexe, et on ne sait pas s'il est fermé. On conjecture que l'ensemble de rotation est une union finie d'intervalles compacts. J'ai d'abord montré ce résultat quand G est le graphe en forme de sigma (un segment recollé à un cercle) ; dans ce cas, on a de plus que tout rationnel dans l'ensemble de rotation est le nombre de rotation d'un point périodique [11]. Dans un deuxième temps, j'ai prouvé la conjecture ci-dessus pour les revêtements universels des graphes en forme de soleil (plusieurs segments disjoints recollés à un cercle) [16]. Pour étudier ces graphes, j'ai construit un graphe symbolique infini permettant de coder les trajectoires de façon appropriée ; cette construction s'inspire des diagrammes de Markov initialement introduits par Hofbauer pour étudier les mesures d'entropie maximale des transformations de l'intervalle monotones par morceaux. Cette voie semble prometteuse pour étudier par la suite l'ensemble de rotation pour des graphes plus généraux.

Ensemble de périodes pour le graphe sigma

Pour tenter de comprendre quels ensembles de période peuvent apparaître pour les transformations de degré 1 sur des graphes ayant une unique boucle, Lluís Alsedà et moi nous sommes attaqués à l'étude des transformations de degré 1 sur le graphe sigma ; les difficultés propres aux graphes apparaissant déjà pour ce graphe. Soit T le revêtement universel du graphe sigma et F une application continue de degré 1 de T dans T. La théorie de rotation développée dans [9] ne concernant que les orbites rencontrant la droite réelle, nous avons étudié séparément les orbites périodiques disjointes de la droite réelle. Soit P une orbite périodique (mod 1) de période p, telle que P n'ait aucun point dans la droite réelle. Nous avons montré, d'une part que l'ensemble des périodes (mod 1) de F contient tous les entiers plus grands que p dans l'ordre de Sharkovskii ; et d'autre part que, si le nombre de rotation de P est 0 et que le diamètre de P est supérieur ou égal à 1, alors pour tout entier strictement positif n, il existe un point périodique de période n et de nombre de rotation 0.

Pour étudier l'ensemble des périodes des orbites périodiques rencontrant la droite réelle, l'idée naturelle est d'essayer de suivre la même démarche que dans le cas du cercle, qui consiste à étudier l'ensemble des périodes pour un nombre de rotation p/q fixé, en se ramenant au cas du nombre de rotation 0. Mais cette démarche se heurte à plusieurs obstacles. Selon le cas général étudié dans [9], si p/q appartient à l'intérieur de RotIR(F), alors il existe N tel que, pour tout n>N, il existe un point périodique de période nq de nombre de rotation p/q. Mais N n'est pas borné, même dans le cas du graphe sigma : pour tout entier naturel N, il existe F avec 0 dans Int(RotIR(F)) et telle que l'ensemble des périodes de nombre de rotation 0 vaut {n > N}. Cependant, nous avons montré que, si 0 est dans Int(RotIR(F)), alors l'ensemble des périodes (mod 1) vaut IN* ou IN*\{1} ou IN*\{2} ; les trois cas sont réalisés. Le fait qu'il s'agisse des périodes (mod 1), et non des périodes de nombre de rotation 0, empêche d'en déduire un résultat pour un nombre de rotation p/q non entier. Concernant les extrémités de l'intervalle de rotation, on trouve, comme on s'y attend, que tout ensemble de périodes d'une transformation de l'étoile à 3 branches peut être réalisé comme ensemble de périodes de nombre de rotation 0 quand min RotIR(F) ou max RotIR(F) vaut 0. Cependant, deux phénomènes se produisent : d'une part, l'ensemble de périodes de nombre de rotation 0 peut être plus compliqué (des exemples montrent notamment qu'il peut correspondre à l'ensemble de périodes d'une transformation d'étoile à n branches avec n arbitrairement grand) ; d'autre part, des obstructions apparaissent pour passer à un nombre de rotation p/q non entier. La situation se révélant bien plus compliquée qu'escomptée, nous n'avons pas obtenu de caractérisation complète de l'ensemble des périodes. Ces travaux sont en cours de rédaction.

Orbites périodiques de grand diamètre

On considère une transformation continue f du cercle dans lui-même, de degré d supérieur ou égal à 1, et F de la droite réelle dans elle-même un relèvement de f. J'ai montré avec Lluís Alsedà que si F a une orbite périodique de diamètre supérieur à 1 (ce qui, pour f, signifie que l'orbite périodique s'étale sur plus d'un tour sur le cercle), alors F a des points périodiques de toutes les périodes, et donc f aussi [10]. Des exemples montrent que ce résultat n'est pas vrai en degré négatif. Cette étude, en plus de son intérêt propre, est surtout motivée par le cas d = 1, qui éclairera peut-être le comportement des transformations de degré 1 sur des graphes. En particulier, pour les relèvements de transformations du graphe sigma, il semble que les orbites de « grand » diamètre forcent l'existence de toutes les périodes supérieures ou égales à 2.

Optimisation

J'ai collaboré à deux reprises avec Olivier Teytaud (Laboratoire de Recherche en Informatique, Orsay) sur des problèmes d'optimisation, sujet assez éloigné de mes thématiques habituelles. Le récent travail [13] est un problème d'extremum dans un cadre matriciel. Le papier [8] concerne l'aspect théorique des algorithmes d'optimisation, les outils mathématiques utilisés sont de l'analyse élémentaire et des probabilités conditionnelles.

Jeu matriciel et équilibre de Nash

Soit M=(mij)i,j une matrice de taille K×K à coefficients dans {0,1} modélisant le jeu à deux joueurs suivant : le joueur « ligne » choisit i dans {1,..., K}, le joueur « colonne » choisit simultanément j dans {1,...,K} ; le joueur « ligne » gagne (et l'autre perd) ssi mij = 1. Soit D l'ensemble des vecteurs de probabilité dans IRK. Une stratégie est un vecteur x dans D (le joueur suivant cette stratégie choisit i avec probabilité xi). Un équilibre de Nash est un couple (x*, y*) dans D2 tel que

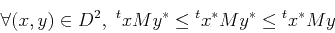
\begin{displaymath}\forall (x,y)\in D^2,\ {}^txMy^*\le {}^tx^*My^*\le {}^tx^*My \end{displaymath}

(autrement dit, aucun des deux joueurs ne peut espérer un meilleur gain moyen en changeant unilatéralement sa stratégie). Il existe toujours au moins un équilibre de Nash. Dans [13], nous nous intéressons au cas où l'équilibre de Nash (x*, y*) est unique et les supports de x* et y* sont de taille k<<K, et on cherche à approximer (x*, y*). Le coeur de l'analyse mathématique consiste à étudier la fonction V(y)= ||My || (la norme est la norme infinie) pour y dans D, dont le minimum est atteint en y*, et à montrer que

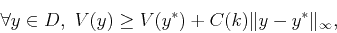
\begin{displaymath}\forall y\in D,\ V(y)\ge V(y^*)+C(k)\Vert y-y^*\Vert _\infty, \end{displaymath}

où C(k) est une constante explicite dépendant uniquement de k. Il existe des algorithmes permettant de trouver un vecteur y tel que V(y) est proche de V(y*). Ce qui précède prouve alors que y est une bonne approximation de y*. De plus, si y est assez proche de y*, on montre que le support de y* est inclus dans {i | yi > d(k)}, pour une constante d(k) explicite. La connaissance du support de y* permet alors une détermination exacte de y*, avec probabilité 1- epsilon, en temps raisonnable par rapport à K (plus précisément, en O(K log(K).k2k)).

Algorithmes d'optimisation à base de comparaisons

Soit D un domaine fixé et F une famille de fonctions f de D dans IR ayant chacune un unique minimum au point x*(f). On cherche à approximer x*(f) par une suite (A(f)_n)n>0 définie par un algorithme déterministe A. Un algorithme à base de comparaisons agit de façon identique sur les fonctions f et g o f quelle que soit la fonction g de IR dans IR strictement croissante. Dans [8], nous avons montré que, quel que soit l'algorithme d'optimisation A, il existe un algorithme A' à base de comparaisons ayant une performance aussi bonne que A par rapport au pire cas dans une famille de fonctions F stable par composition à droite par les fonctions g strictement croissantes. Nous avons également étudié le cas où F est une famille fw dépendant d'un paramètre w dans un espace de probabilité. Dans ce cadre, on peut considérer comme critère de qualité d'un algorithme A, non le pire cas, mais l'espérance E(||A(fw)n - x*(fw)||). O. Teytaud et S. Gelly se sont chargés de la partie expérimentale.

Le chaos pour les transformations de l'intervalle

Une transformation de l'intervalle est un système dynamique défini par une transformation continue d'un intervalle compact dans lui-même. J'ai fait une synthèse des résultats connus concernant le chaos pour les transformations de l'intervalle [livre]. La situation est essentiellement différente du cas général car les diverses notions de chaos coïncident dans une large mesure. Par exemple, la transitivité, qui est considérée comme une hypothèse de base pour obtenir de l'uniformité, engendre un comportement fortement chaotique sur l'intervalle. En effet, elle implique la sensibilité aux conditions initiales et la densité des points périodiques, donc le chaos au sens de Devaney, de même que le chaos générique et une entropie topologique non nulle. De plus, elle est presque équivalente au mélange topologique, qui entraîne à son tour d'autres propriétés (spécification, entropie uniformément positive).

La question qui se pose alors est la suivante : qu'impliquent les différentes propriétés si on ne suppose pas la transitivité ? Pour certaines, comme la sensibilité, le chaos générique ou la densité des points périodiques, on a une réciproque partielle, à savoir qu'il existe une composante transitive composée d'un ou plusieurs sous-intervalles. D'autre part, les diverses périodes des points périodiques pouvant coexister sont régies précisément par l'ordre de Sharkovskii, et le type de points périodiques est lié à l'entropie topologique ; elle est non nulle si et seulement s'il existe un point périodique dont la période n'est pas une puissance de 2. De plus, une entropie non nulle est équivalente à l'existence d'un sous-système chaotique au sens de Devaney et implique le chaos au sens de Li-Yorke. Quant au chaos dense (densité des couples de Li-Yorke dans l'espace produit), j'ai montré qu'il implique une entropie supérieure ou égale à log 2/2 et l'existence d'un point périodique de période 6 [6].

Je me suis également intéressée à l'existence de sous-systèmes transitifs et sensibles aux conditions initiales [5]. Il est connu qu'une transformation de l'intervalle d'entropie non nulle a un sous-système transitif et sensible ; j'ai montré que la réciproque n'est pas vraie. De plus, j'ai démontré que pour une transformation de l'intervalle l'existence d'un tel sous-système entraîne le chaos au sens de Li-Yorke et j'ai construit un contre-exemple montrant que la réciproque est fausse.

Chaînes de Markov topologiques et classification des graphes

Une chaîne de Markov topologique (ou shift de Markov) est un système symbolique défini par l'ensemble des chemins bi-infinis sur un graphe orienté dénombrable, muni de la transformation shift (décalage vers la gauche). Contrairement aux chaînes de Markov probabilistes, il n'y a pas de probabilité a priori. Outre leur intérêt propre, ces systèmes servent d'outil pour l'étude des mesure de probabilité d'entropie maximale (ou mesures maximales) car on connaît des conditions nécessaires et suffisantes pour l'existence et l'unicité de telles mesures ; nous en reparlerons dans la section suivante, dédiée aux mesures maximales pour les transformations de l'intervalle. Quand le graphe est fini, la situation est simple ; en particulier il existe toujours une mesure maximale, qui peut se calculer à partir d'une matrice. Nous ne nous intéressons qu'aux graphes infinis, plus complexes.

Vere-Jones a classé les graphes orientés connexes en trois catégories (transients, récurrents nuls, récurrents positifs) en fonction de critères combinatoires liés au nombre de chemins. En 1970 Gurevich a montré que cette classification est intimement liée à l'existence de mesures d'entropie maximale : si le graphe est connexe, la chaîne de Markov sur ce graphe admet une mesure maximale si et seulement si celui-ci est récurrent positif, et dans ce cas cette mesure est unique et c'est une mesure de Markov ergodique. Il est à noter que pour les graphes récurrents nuls, il existe une mesure infinie jouant le rôle de mesure d'entropie maximale mais dans cette situation l'entropie doit être définie différemment.

J'ai montré que si l'entropie d'une chaîne de Markov topologique sur un graphe connexe est strictement supérieure à son entropie locale alors le graphe est récurrent positif, si bien qu'il existe une mesure d'entropie maximale [3]. Étant donné les liens entre chaînes de Markov topologiques et transformations de l'intervalle, ce résultat conforte la conjecture de Buzzi énonçant que le même résultat est vrai pour les transformations de l'intervalle, mais cette question est toujours ouverte. Signalons que pour les systèmes dynamiques sur un espace métrique compact on sait qu'une entropie locale nulle entraîne l'existence d'une mesure maximale.

Salama a donné une approche géométrique de la classification transient/récurrent nul/récurrent positif en termes d'existence de sous-graphes ou de surgraphes de même entropie : un graphe connexe sans sous-graphe propre de même entropie est récurrent positif, et un graphe connexe est transient si et seulement s'il est strictement inclus dans un graphe transient de même entropie. J'ai complété ces travaux en montrant qu'un graphe transient G peut toujours être inclus dans un graphe récurrent de même entropie, qui est soit récurrent nul soit récurrent positif selon les propriétés de G [3].

Mesures d'entropie maximale pour les transformations de l'intervalle

Une mesure maximale est une mesure de probabilité invariante dont l'entropie réalise le supremum des entropies métriques ; par le principe variationnel son entropie est égale à l'entropie topologique. Les mesures maximales sont particulièrement intéressantes car elles reflètent la totalité de la complexité topologique et permettent de voir où se concentre cette complexité. Elles ont un sens physique moins évident que les mesures absolument continues, par contre elles sont préservées par les conjugaisons par homéomorphisme.

Si f est une transformation de l'intervalle, on peut lui associer un graphe orienté, généralement infini, appelé diagramme de Markov. Cette construction, basée sur la dynamique des sous-intervalles de monotonie, a d'abord été faite par Hofbauer pour les transformations monotones par morceaux, puis généralisée par Buzzi. Sous certaines conditions, la chaîne de Markov topologique sur ce graphe représente l'essentiel de la dynamique de f. En particulier, Buzzi a montré que si f est C 1 et si son entropie est strictement supérieure à l'entropie topologique des points critiques (c'est-à-dire les points au voisinage desquels f n'est pas monotone), alors il y a une bijection entre les mesures maximales ergodiques de f et celles de son diagramme de Markov. Le problème de l'existence de telles mesures pour f se transpose alors sur le graphe.

Une transformation de l'intervalle f qui est soit monotone par morceaux soit $C^{\infty}$ admet au moins une mesure maximale, et cette mesure est unique si f est transitive (résultats de Hofbauer pour le cas monotone par morceaux, Newhouse et Buzzi pour le cas $C^{\infty}$). Ce résultat n'est pas vrai si on suppose seulement f continue, comme l'ont montré Gurevich et Zargaryan. La condition $C^{\infty}$ ne peut pas non plus être affaiblie : pour tout entier n, j'ai construit des transformations de l'intervalle Cn, transitives, mais sans mesure maximale [1]. Pour cela, j'ai utilisé l'approche géométrique de Salama présentée dans la section précédente pour montrer que le graphe de Markov associé à ces transformations est transient ; l'absence de mesure maximale pour le graphe se transporte alors sur l'intervalle.

J'ai déduit des résultats précédents que pour tout entier n il existe des transformations de l'intervalle Cn, transitives, qui ne sont boréliennement conjuguées à aucune transformation $C^{\infty}$ [4].

D'un autre côté, Jérôme Buzzi et moi-même avons montré que la régularité de la transformation permet de donner une condition suffisante d'existence [7], en combinant des résultats liés à la dérivabilité et des propriétés des chaînes de Markov topologiques. On considère f une transformation C 1 de l'intervalle ; on note C l'ensemble des points critiques, htop(C,f) l'entropie de l'ensemble C et hloc(f) l'entropie locale de f. Si l'inégalité htop(f) > htop(C,f) + hloc(f) est vérifiée, alors f a un nombre fini non nul de mesures maximales ergodiques, avec unicité si f est transitive. En utilisant une majoration de l'entropie des zéros de la dérivée et de l'entropie locale, nous obtenons une condition plus facile à vérifier pour les transformations Cr : si

\begin{displaymath} h_{top}(f)> \frac{2}{r} \log \Vert f'\Vert _{\infty}, \end{displaymath}

alors le nombre de mesures maximales ergodiques est fini et non nul.

Couples asymptotiques dans les systèmes d'entropie non nulle

Historiquement, le terme de chaos a été introduit par Li et Yorke pour qualifier le comportement de certains systèmes sur l'intervalle. Par la suite, d'autres définitions du chaos ont été proposées ; elles ne coïncident pas en général, sans qu'aucune puisse figurer comme l'unique « bonne » définition. Il apparaît que la notion de chaos repose plutôt sur un faisceau de propriétés. Il importe d'étudier les relations entre ces propriétés, mais également de savoir dans quelle mesure certains comportements réguliers sont compatibles avec une propriété chaotique donnée.

Soit T une transformation continue de X dans X, où X est un espace métrique compact ; d désigne la distance. Si x et y sont deux points de X, (x,y) est appelé un couple de Li-Yorke si

\begin{displaymath} \limsup_{n\to+\infty}d(T^n x, T^n y)>0\quad\mbox{et}\quad \liminf_{n\to+\infty}d(T^n x, T^n y)=0. \end{displaymath}

Le système (X,T) est dit chaotique au sens de Li-Yorke s'il existe un sous-ensemble non dénombrable S tel que tout couple de points distincts de S est un couple de Li-Yorke. Par ailleurs, (x,y) est un couple asymptotique si

$\displaystyle\lim_{n\to +\infty} d(T^n x,T^n y)=0$;

le couple est propre si x n'est pas égal à y.

J'ai montré avec François Blanchard et Bernard Host qu'un système dynamique (X,T) d'entropie topologique non nulle possède nécessairement des couples asymptotiques propres [2]. Ce résultat répond par la négative à une question de Huang et Ye qui ont étudié les systèmes dont tous les couples de points distincts sont des couples de Li-Yorke et qui se demandaient si de tels systèmes pouvaient avoir une entropie topologique non nulle. Presque au même moment, Blanchard, Glasner, Kolyada et Maass ont montré qu'une entropie non nulle implique le chaos au sens de Li-Yorke. Par conséquent, dans un système d'entropie non nulle il y a cohabitation de couples «chaotiques» (Li-Yorke) et «non chaotiques» (asymptotiques).

Plus précisément, nous avons montré que, pour toute mesure ergodique d'entropie non nulle, presque tout point appartient à un couple asymptotique propre. Si de plus la transformation est inversible, pour presque tout point x il existe un ensemble non dénombrable de points y tels que (x,y) est un couple asymptotique pour T et un couple de Li-Yorke pour T -1, ce qui rappelle les feuilletages stables et instables des Anosov. Les preuves de ces résultats reposent presque exclusivement sur des arguments ergodiques.

Dernière révision : 3 avril 2013.