Questions of algebraic topology in numerical analysis: algorithmics and
applications
conference AMAM du 10 au 13 Février 2003 à Nice
-
Abstract
-
Divergence-free vector fields and their description through stream functions
are difficult to be discretized by means of conforming or non-conforming
finite elements. A spanning-tree technique is then exploited to build up a basis
of the finite-dimensional space of gradient fields and
the edges of the associated co-tree are used to span the space of curl fields.
This strategy is frequently adopted in computational electromagnetics
to state a well-posed vector potential problem.
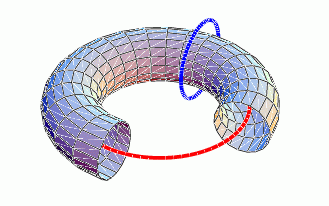
In non-trivial domains (e.g., a torus), the space of gradient fields does not coincide with
the space of curl-free fields. We can span the gradient fields in the torus by means of the
edges of the tree but we have to add the curl-free fields with non-zero circulations
over suitable ``non-bounding loops''.
But how many non-bounding loops are there ? How to find out a set of generators for them ?
Can we do it automatically for non-trivial domains ?
These are typical questions to set for an automated topological solver.
In this minisymposium we aim at discussing on some elementary computational techniques for the
automatic treatment of topological problems arising from potential theory.
The approach is based on computing Smith normal form of the suitable boundary operator matrices.
Other strategies rely on the introduction of suitable ``cuts'' into the domain.
Some applications are then presented.
- Coordinators :
Alain Bossavit
(LGEP),
Francois Dubois
(CNAM),
Francesca Rapetti
(UNSA)
- Speakers
-
- Alain Bossavit
Laboratoire de Génie Electrique de Paris, France.
bossavit@lgep.supelec.fr
- Annalisa Buffa
Istituto di Matematica Applicata e Tecnologie Informatiche, Pavia, Italy.
buffa@ian.pv.cnr.it
-
Patrick Dular
Université de Liège, Belgium.
Patrick.Dular@ulg.ac.be
-
Francesca Rapetti
Laboratoire J.-A. Dieudonné, Université de Nice et Sophia-Antipolis, France.
frapetti@math.unice.fr
-
Isabelle Terrasse
(represented by Axel Tillquin)
European Aeronautic Defence and Space Company, Paris, France.
isabelle.terrasse@eads.net

