TP2 : Étude de pendules.

Exercice 1.- Pendule simple sans frottements.

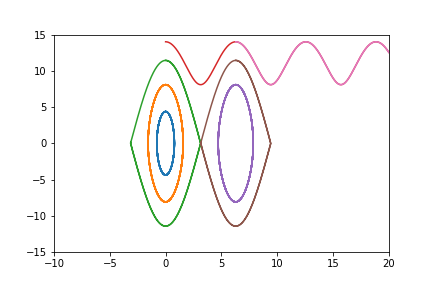
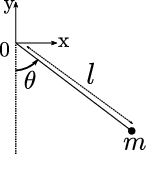
Une masse ponctuelle $m$ est accrochée au bout d'une tige rigide de longueur $l$ (et de masse considérée nulle). On place l'origine du repère au point d'attache de la tige et on note $\theta$ l'angle orienté entre l'axe vertical et la tige. On rappelle que le mouvement du pendule est décrit par l'équation différentielle $$ \tag{E} \theta''(t) + \frac{g}{l} \sin ( \theta(t) ) = 0 \: , $$ où $g = 9.80665$ est l'accélération de la pesanteur à la surface de la Terre. On prendra $l = 0.3$ ($30$ cm). On pose $\omega_0 = \sqrt{\frac{g}{l}}$.

1. En posant $v = \theta^\prime$, mettre l'équation différentielle $(E)$ sous la forme d'un système différentiel $(E_1)$ d'ordre $1$ portant sur $\displaystyle \left( \begin{array}{c} \theta \\ v \end{array} \right)$.

2. Modifier la fonction pointMilieu1D implémentée dans le précédent TP en une fonction pointMilieuMultiD afin de traiter le cas multidimensionnel $y \in \mathbb{R}^d$, $d \in \mathbb{N}^\ast$. La fonction pointMilieuMultiD aura les mêmes arguments et la même structure que dans le cas $1D$, sauf que y0 sera maintant un numpy array. On retrouvera ainsi la dimension $d$ par d = y0.size. La fonction renverra une liste [tps, sol] où tps est toujours le vecteur $[t_0, \ldots, t_N]$ et sol est un numpy ndarray de taille (tps.size, y0.size).

En faisant attention, il suffit de modifier légèrement deux lignes ...

import numpy as np
import matplotlib.pyplot as plt

1. Résoudre numériquement $(E)$ en utilisant le schéma du Point Milieu sur l'intervalle $[0, T]$, avec T = 10 et un pas de temps h = 0.001 et en prenant comme condition initiale $\theta(0) = \pi/4$ et $v(0) = \theta'(0) = 0$. Représenter $\theta$ et $v = \theta^\prime$ en fonction du temps sur une première fenêtre graphique. Recommencer pour différentes valeurs de $\theta(0)$ et $v(0)$.

Lorsque vous définissez secondMembre(t,y), faites attention : y est un numpy.array([theta, v]) de taille $2$ et secondMembre renvoie un numpy array de taille $2$.

1. On veut à présent représenter la solution approchée dans le plan $(\theta, v)$ (aussi appelé plan de phase...). Dans une nouvelle fenêtre graphique, tracer la courbe $(\theta(t), v(t))$, $t \in [0,T]$ ou plus exactement, $t \in $ tps (pour $\theta(0) = \pi/4$ et $v(0) = \theta'(0) = 0$ par exemple). Ajouter sur la même figure les courbes correspondant aux conditions initiales $\theta(0) \in \{ 0, 2\pi \}$ et $v(0) \in \left\lbrace \sqrt{\frac{2g}{l}}, \sqrt{\frac{4g}{l}}, \sqrt{\frac{6g}{l}} \right\rbrace$.

C'est assez simple : si on veut représenter une courbe paramétrée $(x(t), y(t))$ sur un intervalle $t \in [0,T]$ et qu'on connaît $x$ et $y$ sur un vecteur de temps tps qui discrétise régulièrement $[0,T]$, il suffit de tracer y[tps] en fonction de x[tps]. Vous devriez obtenir le tracé suivant, en utilisant la commande plt.axis([-10, 20, -15, 15]) afin d'ajuster la fenêtre :

1. On introduit l'énergie mécanique du pendule $E_m$ qui doit être constante en l'absence de frottements, comme vous l'avez peut-être vu en mécanique un jour ... $$ E_m = \underbrace{\frac{1}{2} m (l \theta^\prime)^2}_{\text{énergie cinétique}} \underbrace{- mg l \cos \theta}_{\text{énergie potentielle}} = m l^2 E(\theta,v) \: . $$ Sur une même figure, représenter l'énergie mécanique du système en fonction du temps pour chacune des solutions calculées à la question précédente.

Pour chaque solution $(\theta, v)$, on demande de représenter $t \in$ tps $\mapsto E(\theta(t), v(t))$.

1. Vérifier que $\displaystyle E(\theta,v) = \frac{1}{2} v^2 - \frac{g}{l} \cos \theta$ est constante le long des solutions $(\theta(t), v(t))_{t \in [0,T]}$ (par un calcul théorique cette fois).

Indication : calculer $\displaystyle \dfrac{d}{dt} E (\theta(t),v(t))$.

1. On appellera orbite $\mathcal{O}_{(\theta_0, v_0)}$ passant par $(\theta_0, v_0)$ l'image de la solution maximale $(\theta, v)$ définie sur un intervalle $J$ et telle que $(\theta(0), v(0)) = (\theta_0, v_0)$, c'est-à-dire $$ \mathcal{O}_{(\theta_0, v_0)} = \{ (\theta(t), v(t)) \in \mathbb{R}^2 \: : \: t \in J \} \: . $$ Utiliser la question précédente pour montrer qu'une orbite de $(E_1)$ est toujours incluse dans une ligne de niveau de $E$ i.e. dans un ensemble de la forme $$ \mathcal{E}_c := \{ (x_1,x_2) \in \mathbb{R}^2 \: : \: E(x_1,x_2) = c \} \quad \text{pour } c \in \mathbb{R} \: . $$ Relier $c$ et $(\theta_0, v_0)$.

1. Représenter sur une première figure quelques lignes de niveaux de $E$ grâce à la fonction plt.contour. Afin de comparer au portrait de phase obtenu à la question $4$, sur une nouvelle figure, représenter les lignes de niveaux correspondant aux orbites représentées à la question $4$ : pour cela, aidez-vous de la relation établie entre $c$ et $(\theta_0, v_0)$ à la question précédente.

Lisez attentivement la section Aide à la fin du notebook concernant plt.contour et np.meshgrid ou utilisez l'aide en ligne de matplotlib.

Exercice 2.- Un pendule double

Le pendule double étudié ici consiste en un pendule (c'est-à-dire une tige de masse nulle et de longueur $l_1$ à laquelle est accrochée une masse $m_1$) à l'extrémité duquel on accroche un autre pendule (tige de longueur $l_2$ à laquelle est accrochée une masse $m_2$). On note $\theta_1$ l'angle que la première tige fait avec l'axe vertical, et $\theta_2$ l'angle que fait la deuxième tige avec l'axe vertical. On placera par la suite l'origine du repère au point d'attache de la première tige.

On admettra que le mouvement du pendule est régi par le système d'équations différentielles $(E_2)$ :

$$ \begin{align*} \theta_1^{''} & = \frac{( - m_2)l_1 \sin( \theta_1 - \theta_2) \cos (\theta_1 - \theta_2) (\theta_1^\prime )^2 - m_2 l_2 \sin (\theta_1 - \theta_2) (\theta_2^\prime )^2 - m_1 g \sin \theta_1 - m_2 g \sin (\theta_1 - \theta_2) \cos (\theta_2)}{l_1 \left(m_1 + m_2 \sin^2 (\theta_1 - \theta_2)\right)} \\ \theta_2^{''} & = \frac{(m_1 + m_2)l_1 \sin( \theta_1 - \theta_2) (\theta_1^\prime )^2 + m_2 l_2 \sin (\theta_1 - \theta_2) \cos (\theta_1 - \theta_2) (\theta_2^\prime )^2 + (m_1 + m_2) g \sin (\theta_1-\theta_2) \cos (\theta_1) }{l_2 \left(m_1 + m_2 \sin^2 (\theta_1 - \theta_2)\right)} \end{align*} $$

1. En posant $v_1 = \theta_1^\prime$ et $v_2 = \theta_2^\prime$, ramener le système $(E_2)$ à un système différentiel $(E_4)$ non linéaire d'ordre $1$ à $4$ équations.

1. On fixe les valeurs des paramètres à l1=1; m1=2; l2=1; m2=1; g=9.80665, définir une fonction penduleDouble qui prend en argument une vecteur de taille $4$ et renvoie un vecteur de taille $4$ définissant le second membre de $(E_4)$. Afin d'éviter les erreurs de saisie on pourra utiliser les lignes suivantes :

# parametres
g = 9.80665
l1 = 1.
l2 = 1.
m1 = 2.
m2 =1.
    
""" En posant y1 = theta1 et y2 = theta2 on donne
theta1'' = ( (-m2)*l1*np.sin(y1-y2)*np.cos(y1-y2)*y3**2 - m2*l2*np.sin(y1-y2)*y4**2 - m1*g*np.sin(y1) - m2*g*np.sin(y1-y2)*np.cos(y2) )/(l1*(m1+m2*np.sin(y1-y2)**2 ))
theta2'' = ( (m1+m2)*l1*np.sin(y1-y2)*y3**2 + m2*l2*np.sin(y1-y2)*np.cos(y1-y2)*y4**2 + (m1+m2)*g*np.sin(y1-y2)*np.cos(y1) )/(l2*( m1+m2*np.sin(y1-y2)**2 ))
"""

" En posant y1 = theta1 et y2 = theta2 on donne\ntheta1'' = ( (-m2)*l1*np.sin(y1-y2)*np.cos(y1-y2)*y3**2 - m2*l2*np.sin(y1-y2)*y4**2 - m1*g*np.sin(y1) - m2*g*np.sin(y1-y2)*np.cos(y2) )/(l1*(m1+m2*np.sin(y1-y2)**2 ))\ntheta2'' = ( (m1+m2)*l1*np.sin(y1-y2)*y3**2 + m2*l2*np.sin(y1-y2)*np.cos(y1-y2)*y4**2 + (m1+m2)*g*np.sin(y1-y2)*np.cos(y1) )/(l2*( m1+m2*np.sin(y1-y2)**2 ))\n"

1. Calculer les coordonnées $(x_1,y_1)$ et $(x_2,y_2)$ de la masse $m_1$ et de la masse $m_2$ dans le repère dont l'origine est le point d'attache du premier pendule. Écrire une fonction coord1 qui prend en argument l'angle $\theta_1$ et renvoie les coordonnées $(x_1,y_1)$ et une fonction coord2 qui prend en argument les angles $\theta_1$ et $\theta_2$ et renvoie les coordonnées $(x_2,y_2)$. Vérifier que vous obtenez bien les coordonnées attendues pour des valeurs de $(\theta_1,\theta_2)$ particulières ($\theta_1=\theta_2=0$ ou $\theta_1=0$ et $\theta_2=\pi/2$ par exemple).

1. On lâche le pendule tendu avec un angle de $60^\circ$ ($\theta_1 (0) = \theta_2(0) = 2\pi/3$) et sans vitesse initiale ($\theta_1^\prime(0)=\theta_2^\prime(0)=0$). Calculer une approximation de l'évolution de $\theta_1$ et $\theta_2$ en utilisant le schéma du Point Milieu, sur un intervalle de temps $[0,20]$ uniformément discrétisé avec un pas de temps $h=0.005$. Représenter les trajectoires $(x_i(t), y_i(t))_{t \in [0,T]}$, $i=1,2$ des masses $m_1$ et $m_2$ obtenues.

1. Pour ceux qui ont le temps. Réaliser une animation montrant le mouvement de l'ensemble du pendule.

Exercice 3.- Pendule amorti

Reprendre l'étude effectuée dans le premier exercice en ajoutant une force de frottement d'intensité proportionnelle (coefficient $k>0$) à la vitesse du pendule : $$ \theta''(t) + k \theta^\prime(t) + \frac{g}{l} \sin ( \theta(t) ) = 0 \:. $$

Aide

Exemples d'utilisation des fonctions np.meshgrid, plt.contour.

• np.meshgrid : la fonction np.meshgridpermet de créer une grille de la fenêtre dans laquelle on souhaite tracer les lignes de niveaux. Étant donnés un np.array x discrétisant les abscisses et un np.array x discrétisant les ordonnées, on va former tous les couples possibles $(x_i, y_j)_{i,j}$ et renvoyer la matrice np.ndarray gx des abscisses ainsi que la matrice np.ndarray gy des ordonnées. Testons sur un exemple :

x = np.linspace(0,5,6)
y = np.linspace(-5,0,6)
gx,gy = np.meshgrid(x,y)

# Voyons ce que ça donne ...
print("x = "+str(x)+"   et   y = "+str(y)+"\n")
print("gx = "+str(gx)+"\n")
print("gy = "+str(gy))

x = [0. 1. 2. 3. 4. 5.]   et   y = [-5. -4. -3. -2. -1.  0.]

gx = [[0. 1. 2. 3. 4. 5.]
 [0. 1. 2. 3. 4. 5.]
 [0. 1. 2. 3. 4. 5.]
 [0. 1. 2. 3. 4. 5.]
 [0. 1. 2. 3. 4. 5.]
 [0. 1. 2. 3. 4. 5.]]

gy = [[-5. -5. -5. -5. -5. -5.]
 [-4. -4. -4. -4. -4. -4.]
 [-3. -3. -3. -3. -3. -3.]
 [-2. -2. -2. -2. -2. -2.]
 [-1. -1. -1. -1. -1. -1.]
 [ 0.  0.  0.  0.  0.  0.]]

On représente ci-dessous les points d'abscisses gx et d'ordonnées gy :

plt.plot(gx,gy,'.r')

[<matplotlib.lines.Line2D at 0x7fbe59c7e070>,
 <matplotlib.lines.Line2D at 0x7fbe59c7e190>,
 <matplotlib.lines.Line2D at 0x7fbe59c7e0a0>,
 <matplotlib.lines.Line2D at 0x7fbe59c7e220>,
 <matplotlib.lines.Line2D at 0x7fbe59c7e2e0>,
 <matplotlib.lines.Line2D at 0x7fbe59c7e3a0>]

• plt.contour : voici un exemple d'utilisation de plt.contour pour représenter des niveaux de la fonction $(x,y) \mapsto x^2 + 2y^2$. On commence par discrétiser la fenêtre dans laquelle on veux tracer les lignes de niveaux à l'aide de meshgrid. Plus on souhaite une précision fine sur les contours, plus il faut choisir une précision fine dans la discrétisation de cette fenêtre : ici concrètement, il faut assez de points dans les vecteurs x et y. Ensuite on évalue la fonction f en tous les points de la grille gx,gy, cela donne une grille de valeurs gz et la fonction plt.contour détermine les lignes de niveaux à partir de ces valeurs. On peut choisir de représenter les niveaux $\{ f(x,y) = c_i \}$, $i = 1, \ldots , m$ en l'indiquant en argument optionnel.

def f(x,y):
    return x**2 + 2*y**2

# Pas assez de points 10 par 10
x = np.linspace(-3,3,10)
y = np.linspace(-5,5,10)
gx, gy = np.meshgrid(x, y)
gz = f(gx, gy)
plt.subplot(1,2,1)
plt.contour(gx, gy, gz)
plt.title("10 par 10 points")

# Plus de points 100 par 100
x = np.linspace(-3,3,100)
y = np.linspace(-5,5,100)
gx, gy = np.meshgrid(x, y)
gz = f(gx, gy)
plt.subplot(1,2,2)
plt.contour(gx, gy, gz)
plt.title("100 par 100 points")

Text(0.5, 1.0, '100 par 100 points')

# On choisit les niveaux 
c = [1, 2, 2*np.pi, 10]
x  = np.linspace(-3,3,100)
y = np.linspace(-5,5,100)
gx, gy = np.meshgrid(x, y)
gz = f(gx, gy)
plt.contour(gx, gy, gz, c)
plt.title('on choisit les niveaux $c_i$')

Text(0.5, 1.0, 'on choisit les niveaux $c_i$')

# On ajoute des labels ...
fig, ax = plt.subplots()
CS = ax.contour(gx, gy, gz, c)
ax.clabel(CS, inline=1, fontsize=10)
ax.set_title('Avec des labels')

Text(0.5, 1.0, 'Avec des labels')