SUJET D'EXAMEN - 27 mai 2022¶

L2 MATHS-INFO - PROGRAMMATION ANALYSE NUMÉRIQUE¶

Durée de l'épreuve 1h30.
Les téléphones portables sont interdits.
Le sujet est constitué de 3 exercices indépendants.

In [1]:
%matplotlib inline
%config InlineBackend.figure_format = 'retina'

import numpy as np
from scipy.integrate import quad
import matplotlib.pyplot as plt

color_bleu = 'xkcd:dusky blue'
color_vert = 'xkcd:grassy green'
color_orange = 'xkcd:orangish'
color_rouge = 'xkcd:blood orange'
color_bleuclair = 'xkcd:sky blue'
color_vertclair = 'xkcd:grass green'
color_marron = 'xkcd:burnt sienna'
color_violet = 'xkcd:blue violet'

liste_color = [
    color_bleu,
    color_vert,
    color_orange,
    color_rouge,
    color_bleuclair,
    color_vertclair,
    color_marron,
    color_violet
]

Exercice 1 : interpolation polynomiale¶

Dans cet exercice, nous cherchons à interpoler une fonction régulière sur l'intervalle $[-2, 10]$. Nous testerons deux fonctions $f$ et $g$ dont les expressions sont $$ f(x) = \cos(x), \qquad g(x) = \frac{\cos(x)}{1+x^2}. $$

Question 1

  1. Définissez les fonctions $f$ et $g$ dans des fonctions python.
  2. Tracez les fonctions dans une fenêtre graphique sur l'intervalle $[-2, 10]$.
In [38]:
def f(x):
    return np.cos(x)

def g(x):
    return np.cos(x)/(1+x**2)

a, b = -2, 10
In [44]:
x = np.linspace(a, b, 1000)
fig = plt.figure(figsize=(6, 6))
ax = fig.add_subplot(1, 1, 1)
for phi in [f, g]:
    ax.plot(x, phi(x), label=f'${phi.__name__}$')
ax.set_title("Les fonctions à interpoler", fontsize=18)
ax.legend();

Question 2 (interpolation de la fonction $f$)

Dans une fenêtre graphique découpée en $4$ axes, un axe pour chaque valeur de $N\in\lbrace 5, 10, 15, 20\rbrace$,

  • tracez le graphe de la fonction $f$ sur l'intervalle $[-2, 10]$ ;
  • ajoutez le nuage de points $(x_i,f(x_i))$, $1\leq i\leq N$, où les $x_i$ sont $N$ points équirépartis sur l'intervalle $[-2, 10]$ ;
  • ajoutez le graphe du polynôme interpolateur de Lagrange aux points $(x_i,f(x_i))$, $1\leq i\leq N$, où les $x_i$ sont $N$ points équirépartis sur l'intervalle $[-2, 10]$ ;
  • ajoutez un titre et une légende.

Que pouvez-vous conclure ? En particulier, la notion d'interpolation coïncident-elle avec la notion d'approximation pour cette fonction ?

In [33]:
def equirepartis(a, b, N):
    """
    retourne les N points équirépartis entre a et b
    
    Parameters
    ----------
    
    a: float
        le bord gauche de l'intervalle
    b: float
        le bord droit de l'intervalle
    N: int
        le nombre de points
        
    Returns
    -------
    
    out: ndarray
        les N valeurs des points équi-répartis
    """
    i = np.arange(1, N+1)
    return a + (b-a)/(N-1) * (i-1)
In [34]:
def interp_Lagrange(x, y, xx):
    """
    calcule et évalue le polynôme interpolateur de Lagrange
    en utilisant la base duale des polynôme de Lagrange
    
    Parameters
    ----------
    
    x: ndarray
        abscisses des points d'interpolation
        
    y: ndarray
        ordonnées des points d'interpolation
        
    xx: ndarray
        abscisses des points d'évaluation
        
    Returns
    -------
    
    yy: ndarray
        ordonnées des points d'évaluation
    """
    if x.size != y.size:
        msg = "Erreur dans interp_Lagrange : x et y doivent avoir la même taille\n"
        msg += f"taille de x : {x.size}\n"
        msg += f"taille de y : {y.size}\n"
        raise ValueError(msg)
    n = x.size
    yy = 0.
    for i in range(n):
        li = 1.
        for j in range(i):
            li *= (xx-x[j]) / (x[i] - x[j])
        for j in range(i+1, n):
            li *= (xx-x[j]) / (x[i] - x[j])
        yy += y[i] * li
    return yy
In [42]:
phi = f
xx = np.linspace(a, b, 1000)

fig = plt.figure(figsize=(12, 12))
fig.suptitle(f"Interpolation de {phi.__name__}", fontsize=20)

for k, N in enumerate([5, 10, 15, 50]):
    ax = fig.add_subplot(2, 2, k+1)
    ax.plot(xx, phi(xx), color=color_vert, linewidth=2, label='fonction')
    ax.set_title(f"$N={N}$", fontsize=18)
    
    x = equirepartis(a, b, N)
    yy = interp_Lagrange(x, phi(x), xx)
    ax.plot(xx, yy, color=color_bleu, label='équirépartis')
    ax.scatter(x, phi(x), color=color_bleu)
    
    ax.set_ylim(-2, 2)
    ax.legend()

Question 3 (interpolation de la fonction $g$)

Recommencez la question précédente avec la fonction $g$. Prenez soin de répondre également à la dernière partie sur le lien entre interpolation et approximation

In [41]:
phi = g
xx = np.linspace(a, b, 1000)

fig = plt.figure(figsize=(12, 12))
fig.suptitle(f"Interpolation de {phi.__name__}", fontsize=20)

for k, N in enumerate([5, 10, 15, 50]):
    ax = fig.add_subplot(2, 2, k+1)
    ax.plot(xx, phi(xx), color=color_vert, linewidth=2, label='fonction')
    ax.set_title(f"$N={N}$", fontsize=18)
    
    x = equirepartis(a, b, N)
    yy = interp_Lagrange(x, phi(x), xx)
    ax.plot(xx, yy, color=color_bleu, label='équirépartis')
    ax.scatter(x, phi(x), color=color_bleu)
    
    ax.set_ylim(-2, 2)
    ax.legend()

Réponse aux questions théoriques :

Dans le premier cas, $f(x)=\cos(x)$, l'interpolation de la fonction par des points équi-répartis semble être une réponse au problème de l'approximation. La raison fondamentale (évoquée en cours) est la régularité de la fonction qui est analytique.

Dans le second cas, $g(x)=\cos(x)/(1+x^2)$, l'interpolation ne répond pas correctement au problème de l'approximation. On observe de grandes oscillations aux bords du domaine dont l'amplitude augmente lorsque le nombre de points augmente. C'est le classique "phénomène de Runge" qui peut apparaitre même pour des fonctions de classe $\mathcal{C}^{\infty}$.

Exercice 2 : intégration numérique¶

Dans cet exercice, nous nous proposons d'implémenter une méthode d'intégration numérique qui utilise les valeurs de la fonction mais aussi celles de sa dérivées.

Nous la testerons sur les fonctions suivantes : $$ f_0(x) = |\sin(\pi x/2)|, \qquad f_1(x) = x |\sin(\pi x/2)|. $$

Question 1 (les fonctions tests)

Les fonctions $f_0$ et $f_1$ ainsi que leur dérivée ont déjà été implantées dans la cellule suivante.

Pour chaque fonction $f\in\lbrace f_0, f_1\rbrace$, tracez dans un graphique

  • la fonction $f$ sur l'intervalle $[-1/2, 1]$,
  • sa dérivée sur le même intervalle
  • ajoutez un titre et des labels
In [2]:
def f_0(x):  # fonction C^0
    return abs(np.sin(.5*np.pi*x))

def df_0(x):
    return (1.*(x>0) - 1.*(x<0)) * .5*np.pi*np.cos(.5*np.pi*x)

def f_1(x):  # fonction C^1
    return x*f_0(x)

def df_1(x):
    return f_0(x) + x*df_0(x)

liste_f = [f_0, f_1]
liste_df = [df_0, df_1]

a, b = -.5, 1
In [3]:
size = 4
x = np.linspace(a, b, 200)
fig = plt.figure(figsize=(size*len(liste_f), size))
fig.suptitle("Les fonctions que l'on va utiliser", fontsize=18)
for k in range(len(liste_f)):
    f, df = liste_f[k], liste_df[k]
    ax = fig.add_subplot(1, len(liste_f), k+1)
    ax.plot(x, f(x), color=color_bleu, linewidth=2, label="fonction")
    ax.plot(x, df(x), color=color_vert, linewidth=2, label="dérivée")
    ax.set_title(f"${f.__name__}\in\mathcal{{C}}^{{{k}}}$", fontsize=16)
    ax.axhline(0, linestyle='dotted', color='black', linewidth=0.5)
    ax.legend()
fig.tight_layout()

Etant donnée une fonction régulière $f:[a, b]\to\mathbb{R}$ (au moins dérivable), nous souhaitons approcher la valeur de $$ I(f) = \int_a^b f(x) \operatorname{d}\!x. $$ Nous définissons un entier $m\in\mathbb{N}^*$, le pas d'espace $h=(b-a)/m$ et les points de discrétisation $$ a_j = a + jh, \qquad 0\leq j \leq m. $$

Une méthode vue en cours consiste à calculer la valeur $I_h$ définie par \begin{equation} I_h = \frac{h}{2} \sum_{j=0}^{m-1} \Bigl( f(a_j)+f(a_{j+1}) \Bigr) . \end{equation}

La méthode proposée consiste à calculer une valeur modifiée notée $\tilde I_h$ définie par \begin{equation} \tilde I_h = I_h + \frac{h^2}{12} \Bigl( f'(a) - f'(b) \Bigr) = \frac{h^2}{12} \Bigl( f'(a) - f'(b) \Bigr) + \frac{h}{2} \sum_{j=0}^{m-1} \Bigl( f(a_j)+f(a_{j+1}) \Bigr) . \end{equation}

Question 2 (implémentation)

  1. Rappelez le nom de la méthode consistant à calculer $I_h$ et donnez (sans démonstration) l'ordre de cette méthode dans le cas où $f$ est une fonction suffisamment régulière.
  2. Proposez une fonction quad_base(f,x) qui prend en argument une fonction f et un tableau x qui contient une subdivision $a_0 < \ldots <a_m$ d'un intervalle $[a,b]$, et retourne la valeur approchée de $I$ obtenue par la formule du cours $I_h$.
  3. Proposez une fonction quad_mod(f,x) qui prend en argument une fonction f et un tableau x qui contient une subdivision $a_0 < \ldots <a_m$ d'un intervalle $[a,b]$, et retourne la valeur approchée de $I$ obtenue par la nouvelle formule proposée $\tilde I_h$.
In [4]:
def quad_base(f, df, x):
    """
    méthode des trapèzes
    
    Parameters
    ----------
    
    f: function
        la fonction que l'on doit intégrer
    x: ndarray
        la discrétisation choisie
        
    Returns
    -------
    
    Ia: float
        la valeur approchée de l'intégrale
        
    Remarks
    -------
    
    Ia = \sum_{i=1}^{x.size-1} .5*(x_i-x_{i-1}) (f(x_{i-1})+f(x_i))
    """
    xp, xm = x[1:], x[:-1]
    return .5*np.sum((xp-xm)*(f(xm)+f(xp)))

def quad_mod(f, df, x):
    """
    méthode des trapèzes modifiée
    
    Parameters
    ----------
    
    f: function
        la fonction que l'on doit intégrer
    df: function
        la dérivée de la fonction que l'on doit intégrer
    x: ndarray
        la discrétisation choisie
        
    Returns
    -------
    
    Ia: float
        la valeur approchée de l'intégrale
        
    Remarks
    -------
    
    Ia = \sum_{i=1}^{x.size-1} .5*(x_i-x_{i-1}) (f(x_{i-1})+f(x_i))
    """
    h = x[1] - x[0]
    return quad_base(f, df, x) + h**2/12*(df(x[0]) - df(x[-1]))

Question 3 (test des méthodes)

  • Calculez et affichez la valeur exacte $I$ pour chaque fonction $f_0$ et $f_1$ donnée par la fonction quad de scipy.integrate (en choissisant une erreur absolue epsabs = 1e-14).
  • Calculez et affichez la valeur approchée $I_h$ et $\tilde I_h$ pour chaque fonction $f_0$ et $f_1$, avec un paramètre $h=0.1$ ($I_h$ pour la méthode quad_base et $\tilde I_h$ pour la méthode quad_mod).
In [8]:
h = 0.1
x = np.arange(a, b+h, h)
for k in range(len(liste_f)):
    f, df = liste_f[k], liste_df[k]
    print("*"*50)
    print(f"Fonction f{k:1d}")
    print("-"*50)
    I = quad(f, a, b, epsabs=1.e-14)[0]
    print(f"Valeur exacte donnée par quad : {I:10.7f}")
    for methode in [quad_base, quad_mod]:
        Ih = methode(f, df, x)
        print(f"Valeur donnée par {methode.__name__:^9s}   : {Ih:10.7f}")
print("*"*50)

**************************************************
Fonction f0
--------------------------------------------------
Valeur exacte donnée par quad :  0.8230814
Valeur donnée par quad_base   :  0.8213883
Valeur donnée par quad_mod    :  0.8204627
**************************************************
Fonction f1
--------------------------------------------------
Valeur exacte donnée par quad :  0.3437842
Valeur donnée par quad_base   :  0.3435656
Valeur donnée par quad_mod    :  0.3437843
**************************************************

Question 4 (courbes d'erreur)

Nous allons à présent tracer une courbe d'erreur pour les deux méthodes pour les comparer.

Répétez les questions suivantes pour chaque fonction $f\in\lbrace f_0, f_1\rbrace$.

  1. Créez un vecteur de taille $8$ noté vh contenant les valeurs $2^{-1}, 2^{-2}, \ldots, 2^{-8}$.

  2. Créez deux vecteurs de taille $8$ notés ehbase et ehmod contenant les erreurs pour chaque méthode, c'est-à-dire tels que $$ \texttt{ehbase[i]} = \lvert I - I_{\texttt{vh[i]}} \rvert, \qquad \texttt{ehmod[i]} = \lvert I - \tilde I_{\texttt{vh[i]}} \rvert. $$ L'intégrale exacte $I$ sera calculée par la fonction quad du module scipy.integrate.

  3. Dans une fenêtre graphique tracez les deux nuages de points d'abscisse vh et d'ordonnées ehbase puis ehmod en échelle logarithmique.

  4. Ajoutez des droites de pente $2$ et $4$.
  5. Ajoutez un titre et une légende.

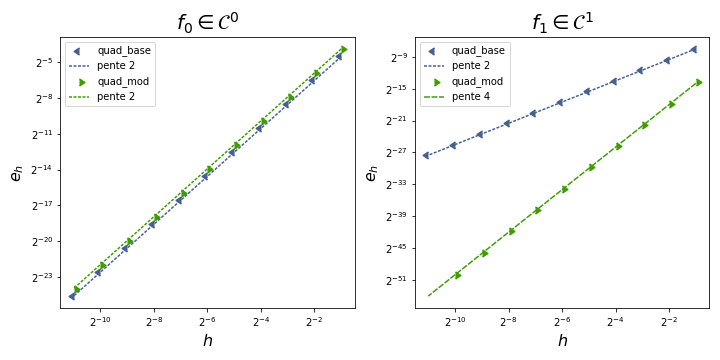
Indication : vous pourrez essayer d'obtenir une figure ressemblant à celle-ci : integration

In [9]:
savename = "ER_integration"
liste_methodes = [quad_base, quad_mod] #, quad_mod2]
liste_p = [[2, 2, 2], [2, 4, 4]]
liste_symb = [8, 9, 10]

taille = 5
fig = plt.figure(figsize=(taille*len(liste_f), taille))
vh = np.array([2**k for k in range(-1, -12, -1)])

for numf in range(len(liste_f)):
    f = liste_f[numf]
    df = liste_df[numf]
    Iex = quad(f, a, b, epsabs=1.e-14)[0]
    ax = fig.add_subplot(1, len(liste_f), numf+1)
    ax.set_xscale('log', base=2)
    ax.set_yscale('log', base=2)

    for k, methode in enumerate(liste_methodes):
        Iap = np.empty(vh.shape)
        for i, h in enumerate(vh):
            x = np.arange(a, b+.5*h, h)
            Iap[i] = methode(f, df, x)
        ve = abs(Iex - Iap)
        ax.scatter(
            vh, ve, c=liste_color[k], s=50,
            label=f"{methode.__name__}",
            marker=liste_symb[k]
        )
        indices = np.logical_and(ve > 1.e-14, ve<2.**-20)
        p = liste_p[numf][k]
        ax.plot(vh, ve[-2]*(vh/vh[-2])**p, label=f'pente {p:1d}', color=liste_color[k], linestyle=(0, (p, 1)))

    ax.set_title(f"${f.__name__}\in\mathcal{{C}}^{{{numf}}}$", fontsize=20)
    ax.set_xlabel(r'$h$', fontsize=16)
    ax.set_ylabel(r'$e_h$', fontsize=16)
    ax.legend()

fig.tight_layout()
if savename is not None:
    fig.savefig(savename + ".png")

Question 5 (Analyse d'ordre)

Analysez les courbes obtenues à la question précédente :

  • Donnez l'ordre de convergence (obtenu numériquement) pour chaque méthode lorsque la fonction est régulière et lorsque la fonction est seulement continue.
  • Précisez les avantages et les inconvénients de la méthode modifiée.
  • La méthode des trapèzes est d'ordre 2 dès que la fonction est continue. Lorsque la fonction est plus régulière, l'ordre est inchangé.
  • La méthode des trapèzes modifiée est d'ordre 4 pour les fonctions de classe $C^1$ et seulement d'ordre 2 si la fonction est seulement continue.
  • L'avantage de la méthode modifiée est qu'une petite correction (ajoute de deux termes supplémentaires par rapport à la méthode des trapèzes) permet d'améliorer grandement l'ordre pour les fonctions régulières.
  • L'inconvénient est qu'il est nécessaire de calculer la dérivée au bord du domaine d'intégration.

Exercice 3 : Recherche d'un zéro d'une fonction¶

Pour cet exercice on fera les tests avec la fonction suivante sur l'intervalle $[-3,3]$ : $$ f(x) = x^3 - x^2/2 + 2x $$

Question 1

  1. Commencez par implémenter cette fonction.
  2. Tracez la afin de vérifier qu'elles possèdent bien un unique 0 dans l'intervalle $[-3,3]$.
  3. Ajoutez un point à la position de ce zéro : sa valeur est évidemment $0$.

Indication : vous pourrez penser à utiliser la commande set_ylim pour bien visualiser la zone autour de l'axe des ordonnées.

In [265]:
def f(x):
    #return x**5 - 5*x**3 + 10*x
    return x**3-.5*x**2+2*x

solution = 0
a = -3
b = 3
In [266]:
size = 6
fig = plt.figure(figsize=(size, size))
x = np.linspace(a, b, 1000)

ax = fig.add_subplot(1, 1, 1)
ax.plot(x, f(x), color=color_rouge, linewidth=2)
ax.scatter([solution], [f(solution)], s=50, color=color_bleu)
ax.set_title(f'${f.__name__}$', fontsize=20, color=color_bleu)
ax.axhline(0, color='black', linestyle='dotted')
ax.set_ylim(-20, 20)
Out[266]:
(-20.0, 20.0)

Nous rappelons que la méthode de la sécante consiste à construire 3 suites $(a_n)$, $(b_n)$ et $(c_n)$ de la manière suivante : nous choisissons $a_0$ et $b_0$ tels que $f(a_0)f(b_0)<0$ (encadrement du zéro recherché). Puis nous définissons $$ c_n = \frac{a_nf(b_n)-b_nf(a_n)}{f(b_n)-f(a_n)}, \quad a_{n+1} = \left\lbrace\begin{aligned} a_n&\text{ si }f(a_n)f(c_n)<0,\\ c_n&\text{ si }f(a_n)f(c_n)\geq0, \end{aligned}\right. \quad b_{n+1} = \left\lbrace\begin{aligned} b_n&\text{ si }f(b_n)f(c_n)<0,\\ c_n&\text{ si }f(b_n)f(c_n)\geq0, \end{aligned}\right. $$

Question 2

Implémentez la méthode de la sécante à travers une fonction x, niter, aL, bL, cL = secante(f, a, b, tol, itermax) qui prend en arguments

  • la fonction $f$ dont on cherche la racine,
  • l'intervalle $[a, b]$ avec $f(a) f(b) < 0$,
  • le paramètre $tol$ du test d'arrêt : on arrête si $|f(x)| < tol$
  • et le nombre $iterMax$ maximum d'itérations autorisées.

et qui retourne :

  • $x$ la solution approchée,
  • $niter$ le nombre d'itérations réalisées,
  • $aL$, $bL$ et $cL$ des ndarray contenant les termes des suites $(a_n)$, $(b_n)$ et $(c_n)$.
In [ ]:
def secante(f, a, b, tol=1e-6, itermax=500):
    """
    Approximation du zeros d'une fonction f passée en argument

    Parameters
    ----------

    f: function
        la fonction
    a: float
        bord gauche de l'intervalle
    b: float
        bord droit de l'intervalle
    tol: float (default 1.e-6)
        paramètre du test d'arrêt : arrêt si |f(x)| < tol
    itermax: int (default 1000)
        nombre maximal d'itération
        
    Returns
    -------
    
    x: float
        la solution approchée trouvée
    niter: int
        le nombre d'itérations
    an: ndarray
        les valeurs de la suite an
    bn: ndarray
    """
    # METTRE LE CODE ICI
    an, bn = (a, b) if a < b else (b, a)
    fan, fbn = f(an), f(bn)
    la, lb, lc = [an], [bn], []
    if fan * fbn > 0:
        raise ValueError(f"Probleme dans fausse position: {a}, {b}")
    niter, fcn = 0, 2*tol
    while abs(fcn) > tol and niter < itermax:
        cn = (an*fbn - bn*fan) / (fbn - fan)
        fcn = f(cn)
        if fan*fcn <= 0:
            bn, fbn = cn, fcn
        if fbn*fcn <= 0:
            an, fan = cn, fcn
        la.append(an)
        lb.append(bn)
        lc.append(cn)
        niter += 1
    cn = (an*fbn - bn*fan) / (fbn - fan)
    lc.append(cn)
    return cn, niter, np.asanyarray(la), np.asanyarray(lb), np.asanyarray(lc)

Question 3

  1. Reprenez les graphiques de la question 1.
  2. Calculez la solution approchée $x^\star$ donnée par la méthode de la sécante et représentez la à l'aide d'un scatter sur la figure.
  3. Sur une autre figure, tracez le nuage de points $(|c_n|, |c_{n+1}|)$. Vous pouvez utiliser une échelle logarithmique ! Les courbes sont-elles cohérentes avec la théorie ? Quelle est l'ordre de la méthode ?

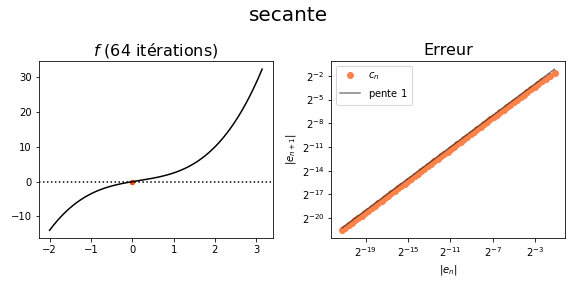
Indication : vous pouvez essayer d'obtenir une figure ressemblant à celle-ci : secante

In [277]:
## METTRE LE CODE ICI

solution = 0
tol = 1.e-6
itermax = 5000
methode = secante

size = 4
fig = plt.figure(figsize=(size*2, size))
fig.suptitle(f"{methode.__name__}", fontsize=20)
x = np.linspace(a, b, 1000)

ax = fig.add_subplot(1, 2, 1)
ax.plot(x, f(x), color='black')
ax.axhline(0, color='black', linestyle='dotted')
title = f'${f.__name__}$'
xstar, niter, aL, bL, cL = methode(f, a, b, tol=tol, itermax=itermax)
title += f" (${niter}$ itérations)"
ax.set_title(title, fontsize=16, color='black')
ax_e = fig.add_subplot(1, 2, 2)
ax_e.set_xscale('log', base=2)
ax_e.set_yscale('log', base=2)
ax.scatter(xstar, f(xstar), s=20, color=color_rouge)
ax_e.scatter(abs(cL[:-1]-solution), abs(cL[1:]-solution), color=color_orange, label=r'$c_n$')
ax_e.plot(abs(cL[:-1]-solution), abs(cL[:-1]-solution), color='black', alpha=0.5, label=r'pente $1$')
ax_e.legend()
ax_e.set_title("Erreur", fontsize=16, color='black')
ax_e.set_xlabel(r"$|e_{n}|$", color='black')
ax_e.set_ylabel(r"$|e_{n+1}|$", color='black')
        
fig.tight_layout()
fig.savefig("ER_secante.png")

Nous proposons alors d'implémenter une méthode inventée en 1979 qui est une amélioration de la méthode de la sécante. Elle consiste à modifier le calcul de la suite $(c_n)$ de la manière suivante. Etant données les valeurs de $a_n$ et de $b_n$, on définit $$ x = \frac{a_n+b_n}{2}, \quad c_n = x + (x-a_n)\frac{f(x)/f(a_n)}{\sqrt{(f(x)/f(a_n))^2-f(b_n)/f(a_n)}}. $$ La suite de l'algorithme est exactement identique.

Question 4

  1. Implémentez cette méthode de la sécante modifiée.
  2. Reprenez la question précédente pour tester cette nouvelle méthode.
  3. Comparez les deux méthodes : quelle est la plus efficace ? Pouvez-vous comparer l'ordre de cette méthode avec une autre méthode vue en cours ? Quel est l'intérêt de cette méthode par rapport à celle vue en cours ?

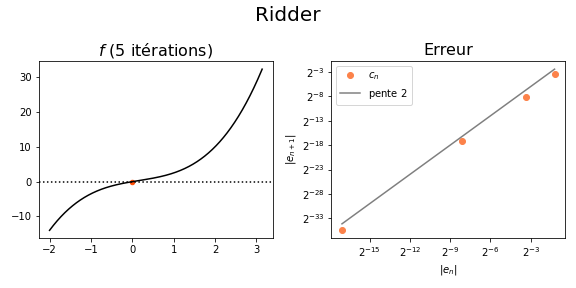
Indication : vous pouvez essayer d'obtenir une figure ressemblant à celle-ci : Ridder

In [275]:
def Ridder(f, a, b, tol=1e-6, itermax=500):
    """
    Approximation du zeros d'une fonction f passée en argument

    Parameters
    ----------

    f: function
        la fonction
    a: float
        bord gauche de l'intervalle
    b: float
        bord droit de l'intervalle
    tol: float (default 1.e-6)
        paramètre du test d'arrêt : arrêt si |f(x)| < tol
    itermax: int (default 1000)
        nombre maximal d'itération
        
    Returns
    -------
    
    x: float
        la solution approchée trouvée
    niter: int
        le nombre d'itérations
    an: ndarray
        les valeurs de la suite an
    bn: ndarray
    """
    # METTRE LE CODE ICI
    an, bn = (a, b) if a < b else (b, a)
    fan, fbn = f(an), f(bn)
    la, lb, lc = [an], [bn], []
    if fan * fbn > 0:
        raise ValueError(f"Probleme dans la méthode de Ridder: {a}, {b}")
    niter, fcn = 0, 2*tol
    while abs(fcn) > tol and niter < itermax:
        x = .5*(an+bn)
        fx = f(x)
        cn = x + (x-an)*fx/fan/np.sqrt((fx/fan)**2-fbn/fan)
        fcn = f(cn)
        #if fcn*fx <= 0:
        #    if x <= cn:
        #        an, fan = x, fx
        #        bn, fbn = cn, fcn
        #    else:
        #        an, fab = cn, fcn
        #        bn, fbn = x, fx
        #else:
        if fan*fcn <= 0:
            bn, fbn = cn, fcn
        if fbn*fcn <= 0:
            an, fan = cn, fcn
        la.append(an)
        lb.append(bn)
        lc.append(cn)
        niter += 1
    return cn, niter, np.asanyarray(la), np.asanyarray(lb), np.asanyarray(lc)
In [278]:
## METTRE LE CODE ICI

solution = 0
tol = 1.e-6
itermax = 5000
methode = Ridder

size = 4
fig = plt.figure(figsize=(size*2, size))
fig.suptitle(f"{methode.__name__}", fontsize=20)
x = np.linspace(a, b, 1000)

ax = fig.add_subplot(1, 2, 1)
ax.plot(x, f(x), color='black')
ax.axhline(0, color='black', linestyle='dotted')
title = f'${f.__name__}$'
xstar, niter, aL, bL, cL = methode(f, a, b, tol=tol, itermax=itermax)
title += f" (${niter}$ itérations)"
ax.set_title(title, fontsize=16, color='black')
ax_e = fig.add_subplot(1, 2, 2)
ax_e.set_xscale('log', base=2)
ax_e.set_yscale('log', base=2)
ax.scatter(xstar, f(xstar), s=20, color=color_rouge)
ax_e.scatter(abs(cL[:-1]-solution), abs(cL[1:]-solution), color=color_orange, label=r'$c_n$')
ax_e.plot(abs(cL[:-1]-solution), abs(cL[:-1]-solution)**2, color='black', alpha=0.5, label=r'pente $2$')
ax_e.legend()
ax_e.set_title("Erreur", fontsize=16, color='black')
ax_e.set_xlabel(r"$|e_{n}|$", color='black')
ax_e.set_ylabel(r"$|e_{n+1}|$", color='black')
        
fig.tight_layout()
fig.savefig("ER_ridder.png")
In [ ]: