SUJET D'EXAMEN - 12 mai 2022

L2 MATHS - PROGRAMMATION ANALYSE NUMÉRIQUE

---

Durée de l'épreuve 1h30.
Les téléphones portables sont interdits.
Le sujet est constitué de 2 exercices indépendants.

---

%matplotlib inline
%config InlineBackend.figure_format = 'retina'

import numpy as np
from scipy.special import j0
import matplotlib.pyplot as plt

color_bleu = 'xkcd:dusky blue'
color_vert = 'xkcd:grassy green'
color_orange = 'xkcd:orangish'
color_rouge = 'xkcd:blood orange'
color_bleuclair = 'xkcd:sky blue'
color_vertclair = 'xkcd:grass green'
color_marron = 'xkcd:burnt sienna'
color_violet = 'xkcd:blue violet'

liste_color = [
    color_bleu,
    color_vert,
    color_orange,
    color_rouge,
    color_bleuclair,
    color_vertclair,
    color_marron,
    color_violet
]

EXERCICE 1 : Intégration Numérique

Dans cet exercice, nous calculons des valeurs approchées de $\pi$ en utilisant la formule $$ 2 \int_0^{+\infty} \frac{1}{1+x^2} \operatorname{d}\!x = \pi. $$

Afin de nous ramener à un intervalle fini (pour appliquer les méthodes du cours), nous définissons $I_N$ comme l'intégrale approchée par la méthode du point milieu à $N^2$ points sur l'intervalle $[0,N]$. C'est-à-dire $$ I_N = \frac{1}{N^2-1} \sum_{k=0}^{N^2-2} f\bigl(\frac{x_{k,N}+x_{k+1,N}}{2}\bigr), $$ avec $$ x_{k,N} = \frac{k}{N^2-1}, \qquad 0\leq k < N^2. $$

• Programmez le calcul de l'intégrale approchée $I_N$ dans une fonction pi_app(N) de paramètre N un entier.
• Dans une fenêtre graphique,
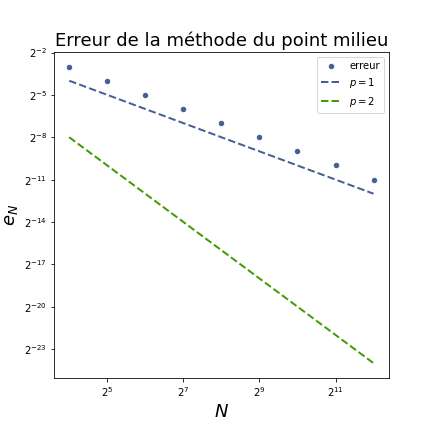
  1. tracez en échelle logarithmique le nuage de points $(N, e_N)$, où $e_N=\lvert I_N-\pi\rvert$, pour $N\in\lbrace 2^4,2^5,\ldots, 2^13\rbrace$ ;
  2. ajoutez des droites de pente $-1$, $-2$ et $-3$ ;
• La convergence vers 0 vous semble-t-elle rapide ? La méthode choisie est-elle efficace ?

Vous pourrez essayer d'obtenir une figure ressemblant à celle-ci :

def quad_milieu(f, x):
    """
    méthode de Simpson
    
    Parameters
    ----------
    
    f: function
        la fonction que l'on doit intégrer
    x: ndarray
        la discrétisation choisie
        
    Returns
    -------
    
    Ia: float
        la valeur approchée de l'intégrale
        
    """
    xp, xm = x[1:], x[:-1]
    return np.sum((xp-xm)*f(.5*(xm+xp)))

def f(x):
    return 1/(1+x**2)

def pi_app(N):
    methode = quad_milieu
    x = np.linspace(0, N, N**2)
    return 2*methode(f, x)

vN, vE = [], []
for n in range(4, 13):
    N = 2**n
    IN = pi_app(N)
    EN = abs(IN-np.pi)
    #print(f"N = 2^{n:02d} : N^2 = 2^{2*n:02d}, I_N = {IN:10.7f}, E_N = {EN:9.3e}")
    vN.append(N)
    vE.append(EN)
vN = np.array(vN)
vE = np.array(vE)

fig = plt.figure(figsize=(6, 6))
ax = fig.add_subplot(1, 1, 1)
ax.set_xscale('log', base=2)
ax.set_yscale('log', base=2)
ax.scatter(vN, vE, s=20, color=color_bleu, label="erreur")
for k, p in enumerate([1, 2]):
    ax.plot(vN, 1/vN**p, linewidth=2, color=liste_color[k], label=f"$p={p}$", linestyle='dashed')
ax.set_title("Erreur de la méthode du point milieu", fontsize=18)
ax.set_xlabel(r"$N$", fontsize=18)
ax.set_ylabel(r"$e_N$", fontsize=18)
ax.legend()
fig.savefig("ES2_int_Q2.png")

EXERCICE 2 : Recherche de 0

Dans cet exercice, nous allons étudier la robustesse de la méthode de Newton en cherchant à déterminer l'unique zéro $x^\star=0$ des fonctions suivantes $$ \begin{aligned} f_0 &= e^x - 1,\\ f_1 &= e^x - 1 + \sin(10\pi x)/100,\\ f_2 &= e^x - 1 + \sin(10\pi x)/20. \end{aligned} $$

Question 1

• Définissez les fonctions $f_0$, $f_1$ et $f_2$, ainsi que leurs dérivés $f'_0$, $f'_1$ et $f'_2$.
• Tracez-les sur l'intervalle $[-1, 1]$.
• Ajoutez un titre, une légende et un point en position $(0,0)$ qui symbolise le zéro cherché.

Vous pourrez essayer de produire une image ressemblant à celle-ci :

def f_0(x):
    return np.exp(x)-1

def f_1(x):
    return np.exp(x)-1+.01*np.sin(10*np.pi*x)

def f_2(x):
    return np.exp(x)-1+.05*np.sin(10*np.pi*x)

def df_0(x):
    return np.exp(x)

def df_1(x):
    return np.exp(x)+.1*np.pi*np.cos(10*np.pi*x)

def df_2(x):
    return np.exp(x)+.5*np.pi*np.cos(10*np.pi*x)

liste_f = [f_0, f_1, f_2]
liste_df = [df_0, df_1, df_2]

taille = 4
a, b = -1, 1
x = np.linspace(a, b, 1024)
fig = plt.figure(figsize=(taille*len(liste_f), taille))
k = 1
for f, df in zip(liste_f, liste_df):
    ax = fig.add_subplot(1, len(liste_f), k)
    ax.plot(x, f(x), color=color_bleu, linewidth=2, label="fonction")
    ax.plot(x, df(x), color=color_orange, linewidth=1, label="dérivée")
    ax.axhline(0, color=color_vert, linestyle='dotted')
    ax.scatter([0], [0], s=20, c=color_rouge)
    ax.set_title(f"${f.__name__}$", fontsize=16)
    ax.set_ylim(-1.5, 4.5)
    ax.legend()
    k += 1
    
fig.savefig("ES2_zero_Q1.png")

Question 2

Avant d'implémenter la méthode de Newton (1) on a besoin de choisir un critère d’arrêt: à chaque itération $k$ de la méthode ce critère nous permet de décider s'il faut caluler l'approximation suivante ou arrêter l'algorithme.

On choisira d’implémenter ici un critère d’arrêt donné par:

\begin{equation} |f(x_k)|< \epsilon \quad \text{ OU } \quad k> N_{max} \end{equation}

où $\epsilon>0$ est un réel fixé et $N_{max} \in \mathbb{N}$ est le nombre maximal d'itérations.

Proposez une fonction newton prenant en arguments

• une fonction $f$
• sa dérivée $f'$
• une condition initiale $x_0$
• une tolérance $\epsilon>0$ pour le critère d’arrêt
• un nombre d'itération maximal $N_{max}$ pour le critère d’arrêt

et qui donne en sortie

• le nombre d'itérations nécessaires pour vérifier le critère d'arrêt,
• la solution approchée $x^*$ calculée avec la méthode de Newton,
• xL un ndarray contenant tous les termes de la suite $(x_n)$ construite par la méthode de Newton.

def newton(f, df, x0, epsilon, Nmax):
    """
    Algorithme de Newton pour résoudre f(x) = 0 
    
    Parameters
    ----------
    f: function
        fonction f
    df: function
        dérivé de f
    x0: float 
        approximation initiale  
    epsilon: float
        tolerance dans le critere d'arret
    Nmax: int
        nombre d'iterations maximal

    Returns
    -------
    niter: float
        nombre d'iteration
    xstar: float
        solution approchée
    xL: ndarray
        la liste des itérés de la méthode
    """
    x = x0
    fx, dfx = f(x), df(x)
    niter = 0
    xL = [x0]
    while abs(fx) >= epsilon and niter < Nmax:
        x -= fx / dfx
        fx, dfx = f(x), df(x)
        niter += 1
        xL.append(x)
    return niter, x, np.asanyarray(xL)

Question 3

1. Reprenez les graphiques de la question 1.
2. Calculez la solution approchée $x^\star$ donnée par la méthode de Newton pour chacun des cas et représentez la à l'aide d'un scatter sur la figure. Pour l'initialisation, vous prendrez $x_0=0.99$.
3. Ajoutez sur chaque figure la ligne brisée $(x_0, 0)$, $(x_0, f(x_0))$, $(x_1, 0)$, $(x_1, f(x_1))$, $\ldots$.
4. Ajoutez un titre contenant le nombre d'itérations obtenus.
5. Que pouvez-vous conclure quant aux liens entre l'efficacité de la méthode de Newton et la convexité ou la monotonie de la fonction ?

Vous pourrez essayer de produire une image ressemblant à celle-ci :

x0 = 0.99
taille = 4
a, b = -1, 1
xx = np.linspace(a, b, 1024)
fig = plt.figure(figsize=(taille*len(liste_f), taille))
k = 1
for f, df in zip(liste_f, liste_df):
    ax = fig.add_subplot(1, len(liste_f), k)
    ax.plot(xx, f(xx), color=color_bleu, linewidth=1, linestyle='dashed', label="fonction")
    ax.plot(xx, df(xx), color=color_orange, linewidth=1, label="dérivée")
    ax.axhline(0, color=color_vert, linestyle='dotted')
    n, x, xL = newton(f, df, x0, 1.e-14, 200)
    ax.scatter([x], [f(x)], s=20, c=color_rouge)
    abscisse = xL.repeat(2)
    ordonnee = f(abscisse)
    ordonnee[::2] = 0
    ax.plot(abscisse, ordonnee, linewidth=1, color=color_violet)
    ax.set_title(f"${f.__name__}$ ({n} itérations)", fontsize=16)
    ax.set_xlim(-1., 1.)
    ax.set_ylim(-1.5, 4.5)
    ax.legend()
    k += 1
    
fig.savefig("ES2_zero_Q3.png")