SUJET D'EXAMEN - 12 mai 2022

L2 INFO - PROGRAMMATION ANALYSE NUMÉRIQUE

---

Durée de l'épreuve 1h30.
Les téléphones portables sont interdits.
Le sujet est constitué de 2 exercices indépendants.

---

%matplotlib inline
%config InlineBackend.figure_format = 'retina'

import numpy as np
from scipy.special import j0
import matplotlib.pyplot as plt

color_bleu = 'xkcd:dusky blue'
color_vert = 'xkcd:grassy green'
color_orange = 'xkcd:orangish'
color_rouge = 'xkcd:blood orange'
color_bleuclair = 'xkcd:sky blue'
color_vertclair = 'xkcd:grass green'
color_marron = 'xkcd:burnt sienna'
color_violet = 'xkcd:blue violet'

liste_color = [
    color_bleu,
    color_vert,
    color_orange,
    color_rouge,
    color_bleuclair,
    color_vertclair,
    color_marron,
    color_violet
]

EXERCICE 1 : Intégration numérique

Dans cet exercice, nous calculons des valeurs approchées de $\pi$ en utilisant la formule $$ \int_{-1}^1 \frac{\operatorname{d}\!x}{\sqrt{1-x^2}} = \pi. $$

Question 1

1. Expliquez pourquoi les formules de Newton-Cotes fermées ne peuvent pas être utilisées.
2. Programmez une fonction quad_milieu(f,x) qui prends un argument une fonction f et un ndarray x qui contient une subdivision $a_0 < \ldots <a_m$ d'un intervalle $[a,b]$, et retourne la valeur approchée de l'intégrale obtenue par la formule du point milieu.
3. Affichez la valeur approchée de $\pi$ trouvée en prenant pour x une subdivision régulière de l'intervalle $[-1,1]$ avec $10$ point.

def quad_milieu(f, x):
    """
    méthode des points milieux
    
    Parameters
    ----------
    
    f: function
        la fonction que l'on doit intégrer
    x: ndarray
        la discrétisation choisie
        
    Returns
    -------
    
    Ia: float
        la valeur approchée de l'intégrale
        
    Remarks
    -------
    
    Ia = \sum_{i=1}^{x.size-1} (x_i-x_{i-1}) f(.5*(x_{i-1}+x_i))
    """
    xp, xm = x[1:], x[:-1]
    return np.sum((xp-xm)*f(.5*(xm+xp)))

f = lambda x: 1/np.sqrt(1-x**2)
Iap = quad_milieu(f, np.linspace(-1, 1, 10))
print(f"La valeur approchée de pi est {Iap:10.7f}")

La valeur approchée de pi est  2.7406308

Question 2

• Créez un tableau vH contenant les valeurs $2^{-3}, 2^{-4}, \ldots, 2^{-19}$.
• Créez un tableau vE de la même taille que celle de vH contenant les valeurs de l'erreur $e_h=\lvert I_h-\pi\rvert$ pour $h$ dans vH. La valeur de $I_h$ est définie comme l'intégrale approchée par la méthode du point milieu avec un vecteur $x$ dont les points sont $x_h=(-1, -1+h, \ldots, 1-h, 1)$.
• Dans une fenêtre graphique,
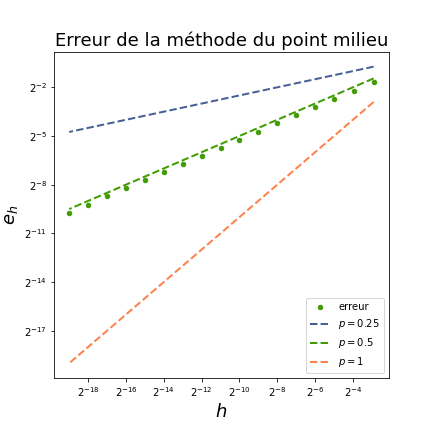
  1. tracez le nuage de points $(h, e_h)$ en échelle logairthmique où $e_h = \lvert I_h-\pi\rvert$ pour $h$ dans vH et $e_h$ dans vE ;
  2. ajoutez des droites de pente $0.25$, $0.5$ et $1$ ;
  3. La convergence vers 0 vous semble-t-elle rapide ? Comparez avec la valeur théorique vue en cours et proposez une explication.

Vous pourrez essayer d'obtenir une figure ressemblant à celle-ci :

vH, vE = [], []
for n in range(4, 21):
    N = 2**n
    x, h = np.linspace(-1, 1, N, retstep=True)
    IN = quad_milieu(f, x)
    EN = abs(IN-np.pi)
    # print(f"N = 2^{n:02d} : I_N = {IN:10.7f}, E_N = {EN:10.3e}")
    vH.append(h)
    vE.append(EN)
vH = np.array(vH)
vE = np.array(vE)
    
fig = plt.figure(figsize=(6, 6))
ax = fig.add_subplot(1, 1, 1)
ax.set_xscale('log', base=2)
ax.set_yscale('log', base=2)
ax.scatter(vH, vE, s=20, color=color_vert, label="erreur")
for k, p in enumerate([.25, .5, 1]):
    ax.plot(vH, vH**p, linewidth=2, color=liste_color[k], label=f"$p={p}$", linestyle='dashed')
ax.set_title("Erreur de la méthode du point milieu", fontsize=18)
ax.set_xlabel(r"$h$", fontsize=18)
ax.set_ylabel(r"$e_h$", fontsize=18)
ax.legend()
fig.savefig("ES1_int_Q2.png")

EXERCICE 2 : Recherche de 0

Les modes propres d'un tambour circulaire sont reliés aux zéros de la fonction de Bessel de première espèce notée $J_0$. Il n'existe pas d'expression simple de cette fonction, seulement une écriture comme une série entière ou encore comme une intégrale.

Dans cet exercice, nous allons chercher à déterminer les premiers zéros de cette fonction. Heureusement pour nous, le module scipy.special est capable de calculer une valeur approchée très précise de $J_0(x)$ quelle que soit la valeur de $x$, même pour $x$ un ndarray. Il faut pour cela taper les commandes

from scipy.special import j0
print(j0(0))

Question 1

Visualisation du graphe de la fonction $J_0$. Dans une fenêtre graphique,

• tracez le graphe de la fonction $J_0$ sur l'intervalle $[0, 20]$
• ajoutez la droite d'équation $y=0$,
• ajoutez un titre

Vous pourrez essayer de produire une figure ressemblant à celle-ci

x = np.linspace(0, 20, 1000)
y = j0(x)

fig = plt.figure(figsize=(5, 5))
ax = fig.add_subplot(1, 1, 1)
ax.plot(x, j0(x), color=color_bleu, linewidth=2)
ax.axhline(0, color=color_vert, linestyle='dotted')
ax.set_title(r"Fonction $J_0$", fontsize=16)
fig.savefig("ES1_zero_Q1.png")

Question 2

Dans un premier temps, nous allons chercher à encadrer les 4 premiers zéros de la fonction $J_0$.

• En regardant la figure de la question précédente, proposez un encadrement grossier (de longueur 3 par exemple) des 4 premiers zéros de la fonction $J_0$.

• Implémentez la méthode de Dichotomie à travers une fonction dichotomie(f, a, b, tol) qui prend en arguments

  • la fonction $f$ dont on cherche la racine,
  • l'intervalle $[a, b]$ avec $f(a) f(b) < 0$,
  • le paramètre $tol$ du test d'arrêt

  et qui retourne deux réels an et bn qui encadrent le zéro de f avec bn-an < tol.

• Déterminez à l'aide de la fonction dichotomie un encadrement des 4 premiers zéros de $J_0$ avec tol=0.25.

def dichotomie(f, a, b, tol=1e-6):
    """
    Approximation du zeros d'une fonction f passée en argument

    Parameters
    ----------

    f: function
        la fonction
    a: float
        bord gauche de l'intervalle
    b: float
        bord droit de l'intervalle
    tol: float (default 1.e-6)
        paramètre du test d'arrêt : arrêt si |f(x)| < tol ou si longueur de l'intervalle < tol
    itermax: int (default 1000)
        nombre maximal d'itération
        
    Returns
    -------
    
    a: float
        bord gauche de l'intervalle
    b: float
        bord droit de l'intervalle
    """
    # METTRE LE CODE ICI
    an, bn = (a, b) if a < b else (b, a)
    fan, fbn = f(an), f(bn)
    if fan * fbn > 0:
        raise ValueError(f"Probleme dans dichotomie: {a}, {b}")
    niter, fcn = 0, 2*tol
    itermax = 1000
    while bn-an > tol and niter < itermax:
        cn = .5*(an+bn)
        fcn = f(cn)
        if fan*fcn <= 0:
            bn, fbn = cn, fcn
        if fbn*fcn <= 0:
            an, fan = cn, fcn
        niter += 1
    return an, bn

liste_0 = [[0, 4], [4, 7], [7, 10], [10, 13]]
liste_1 = []

for bornes in liste_0:
    a, b = bornes
    a, b = dichotomie(j0, a, b, tol=0.25)
    liste_1.append([a, b])

print(liste_1)

[[2.25, 2.5], [5.5, 5.6875], [8.5, 8.6875], [11.6875, 11.875]]

Nous allons ensuite améliorer l'estimation des différents zéros de la fonction $J_0$, nous allons utiliser une seconde méthode.

Afin de ne pas utiliser l'expression de la dérivée de la fonction $J_0$, on peut penser utiliser la méthode de la corde. On se donne $a$ et $b$ qui encadre un zéro de $J_0$ et on pose $q=\frac{J_0(b)-J_0(a)}{b-a}$. A partir de $x_0=a$, on construit la suite définie par $$ x_{n+1} = \phi(x_n) = x_n - J_0(x_n) / q. $$ Cette méthode ressemble à la méthode de Newton mais sans utiliser la dérivée.

Question 3

Avant d'implémenter la méthode de la corde on a besoin de choisir un critère d’arrêt: à chaque itération $k$ de la méthode ce critère nous permet de décider s'il faut calculer l'approximation suivante ou arrêter l'algorithme.

On choisira d’implémenter ici un critère d’arrêt donné par:

\begin{equation} |f(x_k)|< \epsilon \quad \text{ OU } \quad k> N_{max} \end{equation}

où $\epsilon>0$ est un réel fixé et $N_{max} \in \mathbb{N}$ est le nombre maximal d'itérations.

Proposez une fonction corde prenant en arguments

• une fonction $f$
• la pente de la première corde $q$
• une condition initiale $x_0$
• une tolérance $\epsilon>0$ pour le critère d’arrêt
• un nombre d'itération maximal $N_{max}$ pour le critère d’arrêt

et qui donne en sortie

• le nombre d'itérations nécessaires pour vérifier le critère d'arrêt,
• la solution approchée $x^*$ calculée avec la méthode de la corde,
• xL un ndarray contenant tous les termes de la suite $(x_n)$ construite par la méthode de la corde.

def corde(f, q, x0, epsilon, Nmax):
    """
    Algorithme de la corde pour résoudre f(x) = 0 
    
    Parameters
    ----------
    f: function
        fonction f
    q: float
        pente de la première corde
    x0: float 
        approximation initiale  
    epsilon: float
        tolerance dans le critere d'arret
    Nmax: int
        nombre d'iterations maximal

    Returns
    -------
    xstar: float
        solution approchée
    """
    x = x0
    fx = f(x)
    niter = 0
    xL = [x]
    while abs(fx) >= epsilon and niter < Nmax:
        x -= fx / q
        fx = f(x)
        niter += 1
        xL.append(x)
    return niter, x, np.asanyarray(xL)

Question 4

Afin de tester l'algorithme de la corde, nous allons utiliser la fonction $f(x)=e^x-1$ et nous prendrons $a=-1$ et $b=3$.

Sur une figure tracez en échelle logarithmique

• le nuage de points $(e_n, e_{n+1})$, où $e_n = \vert x_n \vert$ est l'erreur commise par la méthode de la corde à l'étape $n$ ;
• une droite de pente 1.

Que pouvez-vous conclure sur l'efficacité de la méthode de la corde dans le cas d'une fonction convexe ? Comparez en particulier avec la méthode de Newton.

Vous pourrez essayer de produire une figure ressemblant à celle-ci :

f = lambda x: np.exp(x) - 1
a, b = -1, 3
epsilon, Nmax = 1.e-10, 1000
q = (f(a)-f(b))/(a-b)
niter, xstar, xL = corde(f, q, b, epsilon, Nmax)
eL = abs(xL)

fig = plt.figure(figsize=(6, 6))
ax = fig.add_subplot(1, 1, 1)
ax.set_xscale('log', base=10)
ax.set_yscale('log', base=10)
ax.scatter(
    eL[:-1], eL[1:],
    color=color_orange, label='Corde'
)
eL = eL[eL>0]
p = 1 #np.polyfit(np.log(eL[:-1]), np.log(eL[1:]), 1)[0]
ax.plot(
    eL[:-1], eL[1]*(eL[:-1]/eL[0])**p,
    color='black', alpha=0.5, label=f'pente ${p}$'
)
ax.legend()
ax.set_title(f"${niter}$ itérations", fontsize=16, color='black')
ax.set_xlabel(r"$|e_{n}|$", color='black')
ax.set_ylabel(r"$|e_{n+1}|$", color='black')
fig.savefig("ES1_zero_Q4.png")

Question 5

• Grâce à l'algorithme de la corde initialisée avec les intervalles trouvés à la question 1 par la méthode de la dichotomie, déterminez une valeur approchée des 4 premiers zéros de la fonction $J_0$ en prenant comme valeur de tolérance $\epsilon=10^{-14}$.
• Affichez les valeurs trouvées ainsi que le nomre d'itérations suivant le format ci-dessous :

  Zéro numéro 0:  2.40482555769577 (8 itérations)
  Zéro numéro 1:  5.52007811028631 (8 itérations)
  ...

for k, bornes in enumerate(liste_1):
    a, b = bornes
    q = (j0(a)-j0(b))/(a-b)
    n, x, _ = corde(j0, q, b, 1.e-15, 100)
    print(f"Zéro numéro {k}: {x:17.14f} ({n} itérations)")

Zéro numéro 0:  2.40482555769577 (8 itérations)
Zéro numéro 1:  5.52007811028631 (8 itérations)
Zéro numéro 2:  8.65372791291101 (6 itérations)
Zéro numéro 3: 11.79153443901428 (5 itérations)