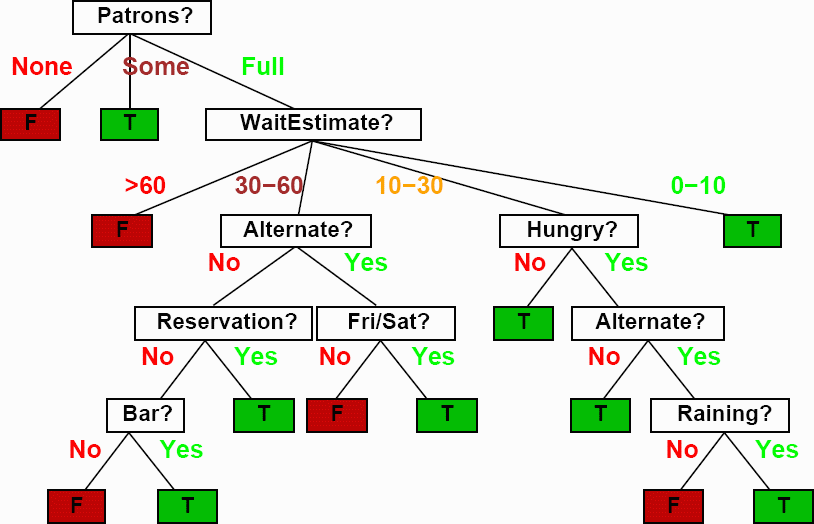
Optimisation des requêtes

Cours basé en grande partie sur ce guide
(Parcourir éventuellement aussi cet article)
Index
SELECT *
FROM joueurs
WHERE id = 32 --id = primary key- Parcours de la table ligne par ligne ?
- ...Mieux ?
Arbre ordonné
Chaque noeud "trie" ses sous-arbres par valeurs de clés
Chaque clé est associée à une adresse mémoire :
celle de la donnée recherchée
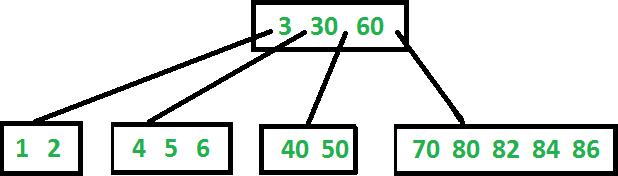
B-tree
Arbre ordonné avec des contraintes particulières (efficacité)
B-tree d'ordre $m$
Arbre satisfaisant les propriétés suivantes (D. Knuth).
- Every node has at most $m$ children.
- Every non-leaf node (except root) has at least $\left \lceil \frac{m}{2} \right \rceil$ children.
- The root has at least two children if it is not a leaf node.
- A non-leaf node with $k$ children contains $k-1$ keys.
- All leaves appear in the same level.
Illustrations
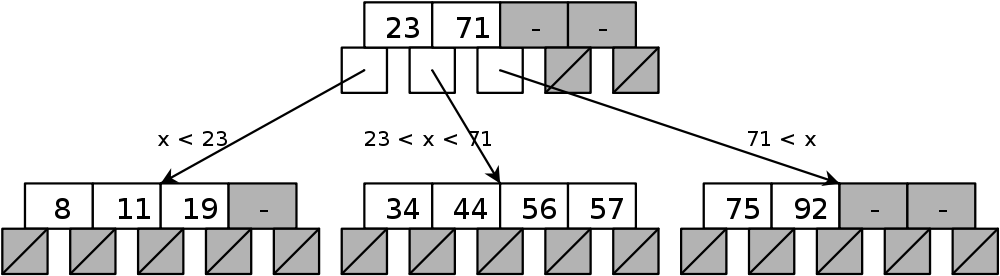
Propriétés
Hauteur bornée (Cormen et al.)
$n$ = nombre maximal de clés contenues dans l'arbre $$\lceil \log_m(n+1) \rceil \leq h \leq \left\lfloor \log_{\lceil m/2 \rceil} \left( \frac{n+1}{2} \right) \right\rfloor$$
Complexité recherche / insertion / suppression : $O(h)$
Remarque : l'insertion et la suppression ne sont pas triviales
Bilan
[Wikipedia]a B-tree:
- keeps keys in sorted order for sequential traversing
- uses a hierarchical index to minimize the number of disk reads
- uses partially full blocks to speed insertions and deletions
- keeps the index balanced with an elegant recursive algorithm
In addition, a B-tree minimizes waste by making sure the interior nodes are at least half full. A B-tree can handle an arbitrary number of insertions and deletions.
Index de BdD
Structure de données utilisée et entretenue par le système de gestion de base de données (SGBD) pour lui permettre de retrouver rapidement des enregistrements.
- Distinct structure in the database that is built using the
create indexstatement. - Requires its own disk space and holds a copy of the table data.
Inconvénient : il faut mettre à jour les index à chaque insertion / suppression $\Rightarrow$ utiliser un B-tree (par exemple) réduit les coûts.
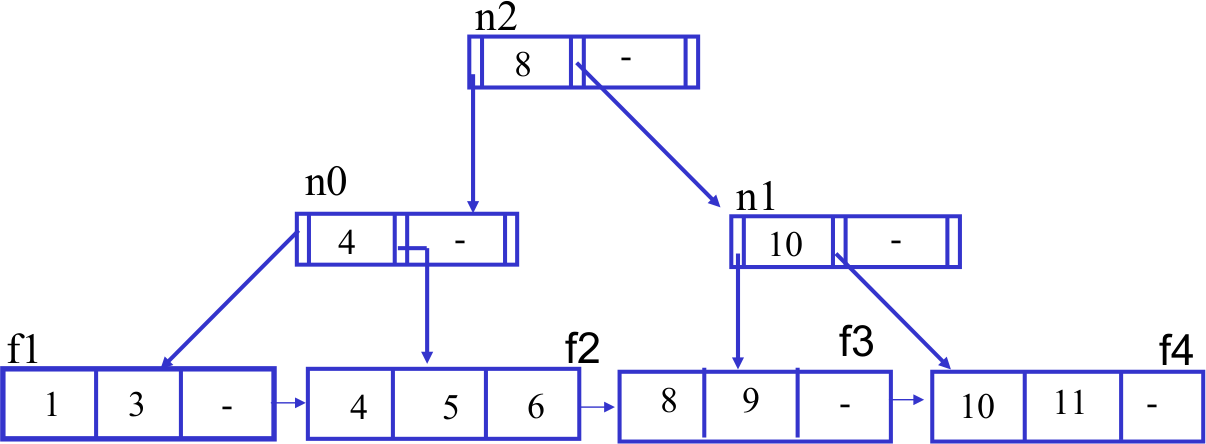
Feuilles du B-tree
Reliées par une structure de liste doublement chaînée.
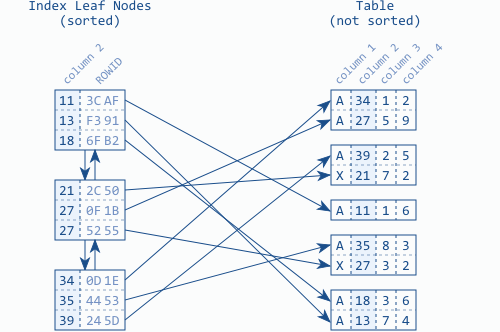
$\Rightarrow$ The index order is maintained on two different levels: the index entries within each leaf node, and the leaf nodes among each other using a doubly linked list
B-tree: Balanced search tree
Balanced : toutes les feuilles ont la même profondeur
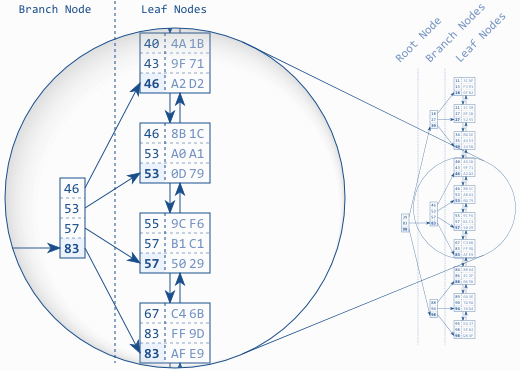
- Doubly linked list: logical order between the leaf nodes.
- Root and branch nodes: quick searching among the leaf nodes.
Each branch node entry corresponds to the biggest value in the respective leaf node.
Syntaxe sqlite3
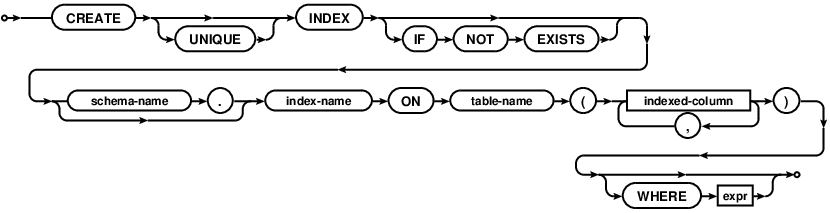
Exemples
CREATE TABLE test(a INTEGER, b INTEGER, c TEXT);
INSERT INTO test VALUES (1,2,'3'),(2,3,'1'),(3,2,'1');
EXPLAIN QUERY PLAN SELECT * FROM test WHERE a = 1;0|0|0|SCAN TABLE testCREATE UNIQUE INDEX a_idx ON test(a);
EXPLAIN QUERY PLAN SELECT * FROM test WHERE a = 1; --and ...0|0|0|SEARCH TABLE test USING INDEX a_idx (a=?)EXPLAIN QUERY PLAN SELECT a FROM test WHERE b = 1;0|0|0|SCAN TABLE testDocumentation du "EXPLAIN QUERY PLAN"
UNIQUE constraint + PRIMARY KEY = auto-indexé
--Table "joueurs" du TP 4
EXPLAIN QUERY PLAN
SELECT "prénom" FROM joueurs WHERE nom = 'Tiviakov';0|0|0|SEARCH TABLE joueurs USING COVERING INDEX
sqlite_autoindex_joueurs_1 (nom=?)EXPLAIN QUERY PLAN
SELECT * FROM joueurs WHERE nom = 'Tiviakov';0|0|0|SEARCH TABLE joueurs USING INDEX
sqlite_autoindex_joueurs_1 (nom=?)EXPLAIN QUERY PLAN
SELECT * FROM joueurs WHERE "prénom" = 'Judit';0|0|0|SCAN TABLE joueurs$\Rightarrow$ L'ordre des colonnes indexées est important
WITH Moro AS (SELECT id FROM joueurs WHERE nom = 'Morozevich')
SELECT sum(
(blancs = Moro.id and "résultat"='1-0') or
(noirs = Moro.id and "résultat"='0-1'))
+ 0.5 * sum(Moro.id IN (blancs,noirs) and "résultat"='1/2')
FROM Moro CROSS JOIN parties p
JOIN tournois t ON p.id_tournoi = t.id
WHERE t.nom = 'Sarajevo' and t."année" = 1999;
0|0|0|SEARCH TABLE joueurs USING COVERING INDEX
sqlite_autoindex_joueurs_1 (nom=?)
0|1|1|SCAN TABLE parties AS p
0|2|2|SEARCH TABLE tournois AS t USING
INTEGER PRIMARY KEY (rowid=?)La table "parties" est parcourue entièrement alors que seules quelques lignes nous intéressent...
.timer on --puis exécution
Run Time: real 0.008 user 0.002347 sys 0.000796Réécriture
WITH Moro AS (SELECT id FROM joueurs WHERE nom = 'Morozevich'),
Sara AS (select id FROM tournois WHERE nom = 'Sarajevo'
AND "année" = 1999)
SELECT sum("résultat"<>'1/2') + .5 * sum("résultat"='1/2')
FROM Moro CROSS JOIN Sara JOIN parties p
ON p.id_tournoi = Sara.id AND (
(p.blancs=Moro.id AND p."résultat"='1-0') OR
(p.noirs=Moro.id AND p."résultat"='0-1') OR
(Moro.id IN (p.blancs, p.noirs) AND p."résultat"='1/2'));
0|0|0|SEARCH TABLE joueurs USING COVERING INDEX
sqlite_autoindex_joueurs_1 (nom=?)
0|1|1|SEARCH TABLE tournois USING COVERING INDEX
sqlite_autoindex_tournois_1 (nom=? AND année=?)
0|2|2|SEARCH TABLE parties AS p USING INDEX
sqlite_autoindex_parties_1 (id_tournoi=?)Run Time: real 0.001 user 0.001002 sys 0.000024$\Rightarrow$ Gain d'un facteur 8 !
D'autant plus significatif que la table "parties" est grande.
Big Query ...sur Big Data
Données qui ne tiennent pas en RAM (de l'ordre du To ou +)
SQL usuel, mais attention au volume de données scannées.
En particulier :
LIMIT nretourne seulement $n$ lignes mais après avoir tout scannéa JOIN b ON cexplose si $c$ n'est pas assez restrictive
An SQL query walks into a bar and sees two tables.
He walks up to them and asks 'Can I join you?'
— Source: Unknown
Associativité : $$\begin{align*} \text{a JOIN b JOIN c} &= \text{(a JOIN b) JOIN c}\\ &= \text{a JOIN (b JOIN c)} \end{align*}$$ SQLite choisit un ordre ou l'autre suivant le coût estimé.
Placer les tables par taille croissante de gauche à droite
Conseils (expliqués par index)
Utiliser LIKE pour rechercher par préfixe :
SELECT * FROM t WHERE a LIKE 'Cou%': OKSELECT * FROM t WHERE a LIKE '%cou': Bad
...De préférence sur un champ indexé
Éviter si possible les sous-requêtes corrélées :
SELECT employee_number, name,
(SELECT AVG(salary)
FROM employees
WHERE department = emp.department) AS department_average
FROM employees AS emp;Devient :
SELECT employees.employee_number, employees.name
FROM employees INNER JOIN
(SELECT department, AVG(salary) AS department_average
FROM employees
GROUP BY department) AS temp
ON employees.department = temp.department
WHERE employees.salary > temp.department_average;Éviter les fonctions à gauche du signe = (lvalue) :
SELECT * FROM t
WHERE substr(a,0,3) = 'Hel';Devient :
SELECT * FROM t
WHERE a like 'Hel%';Éviter d'utiliser "OR" (si possible...)
SELECT * FROM t
WHERE a = 32 or a = 42;Devient :
SELECT * FROM t
WHERE a IN (32,42);De même, a > 0 AND a < 10
devient a BETWEEN 0 AND 10
Éviter d'utiliser HAVING (si possible...)
SELECT a FROM t WHERE c
GROUP BY a HAVING a > 32Devient :
SELECT a FROM t WHERE c AND a > 32
GROUP BY aÉviter le SELECT DISTINCT (qui re-scanne et supprime les doublons)
Éviter d'utiliser NOT IN (...)
$\rightarrow$ Essayer de remplacer par IN
Mais, surtout...
N'optimiser que si nécessaire ☺
(i.e. si lenteurs constatées, et si elles viennent du SGBD)
CREATE UNIQUE INDEX employee_pk
ON employees (subsidiary_id, employee_id)SELECT first_name, phone_number
FROM employees
WHERE last_name = 'WINAND' AND subsidiary_id = 30Plus lent avec l'index si beaucoup d'employés ont
subsidiary_id = 30 (pourquoi ?)
Maximiser les tâches réalisées par une requête
$\Rightarrow$ moins d'allers-retours avec le SGBD.
...Ne pas lui en demander trop non plus :
SELECT value,
(SELECT sum(t2.value) FROM t t2
WHERE t2.value <= t.value) AS accumulated
FROM t;Complexité $O(n^2)$ ☹
Mieux (mais pas SQLite) :
SELECT value,
sum(value) OVER (ORDER BY value)
FROM t;Algorithmes
Jointures
Nested JOIN
Pour chaque ligne de la table 1, chercher toutes les lignes correspondantes.
Algorithme correspondant au processus mental, mais peu efficace : $O(n \times m)$
Intéressant néanmoins si une table est de très petite taille, ou pour obtenir les $k$ premières lignes du résultat très rapidement.
Merge JOIN
Les tables sont triées selon les colonnes de jointures (déjà fait si index), puis un scan linéaire des index est réalisé.
Intéressant si au moins une table est déjà indexée, et si la table non indexée est (relativement) petite.
Complexité $O([\log m] m + [\log n] n)$
Hash JOIN
Utilise une table de hachage regroupant les lignes de la plus petite table (sur la condition de jointure)
Une fois cette structure construite (en RAM), il suffit de parcourir l'autre table.
Complexité $O(m+n)$ en général
Insertion dans un B-tree
$\rightarrow$ Toujours dans une feuille
Pour s'assurer qu'une insertion est toujours possible sans "remonter", on peut diviser chaque noeud plein rencontré sur le chemin.

Suppression dans un B-tree
$\rightarrow$ dans une feuille ou noeud intermédiaire...
Bloom filters
Ingrédients : un ensemble $E$ et...
- $k$ fonctions de hachage $E \rightarrow \{0,1\}$,
- un tableau de bits de taille $m$.

Probabilité de faux positif : $$\simeq (1 - e^{-kn / m})^k$$