Plan du cours
- Conception BD part I : MCD
- Conception BD part II : MLD, implémentation
- Requêtes SQL part I, algèbre relationnelle
- Requêtes SQL part II, triggers
- Index, optimisation de requêtes
- NoSQL part I : MongoDB
- NoSQL part II : HBase, Redis
Conception d'une base de données

Cours basé sur ce document et cette doc.
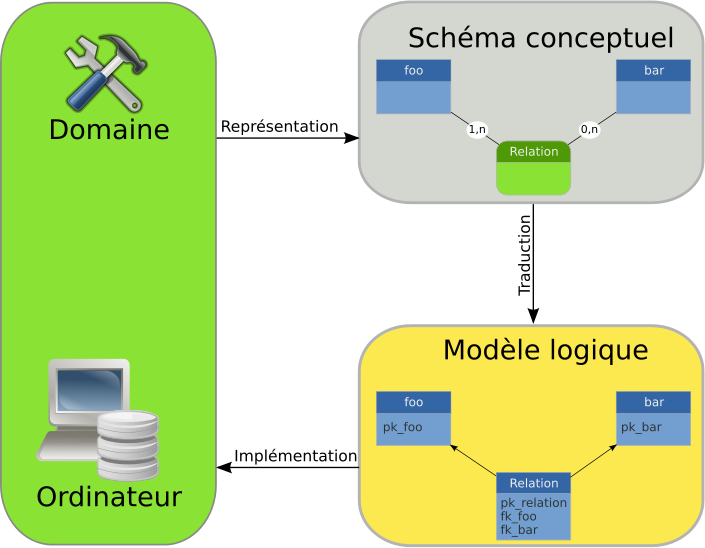
Modèle conceptuel des données
Schéma entité-association
(Type-)Entité = population d'individus homogènes.
Exemple : clients, produits, fournisseurs...
(Type-)Association = lien logique entre plusieurs entités.
Exemple : acteur — jouer dans — film.

Remarque : pas de lien direct client — fournisseur.
Attributs et identifiants
Attribut = propriété d'une entité ou d'une association.
Exemple pour un article : prix, date de péremption...
Identifiant = attribut unique pour une (instance d') entité.
Exemples : numéro de client, numéro de commande.

Remarques :
- une entité possède au moins un attribut (son identifiant) ;
- une association peut être dépourvue d'attribut.
Entité faible
Une entité est faible si sa clé contient un attribut d'une autre entité, ou + généralement si elle n'a de sens qu'en lien avec une autre entité.
Cardinalités
La cardinalité d'un lien entre une entité et une association précise le minimum et le maximum de fois qu'un individu de l'entité peut être concerné par l'association $-$ dans un certain contexte.

- un client peut commander combien d'articles ? (au moins un) ;
- un article est commandé par combien de clients ? ($[0,+\infty[$) ;
- un article est livré par combien de fournisseurs ? (au moins un) ;
- un fournisseur livre combien d'articles ? (au moins un).
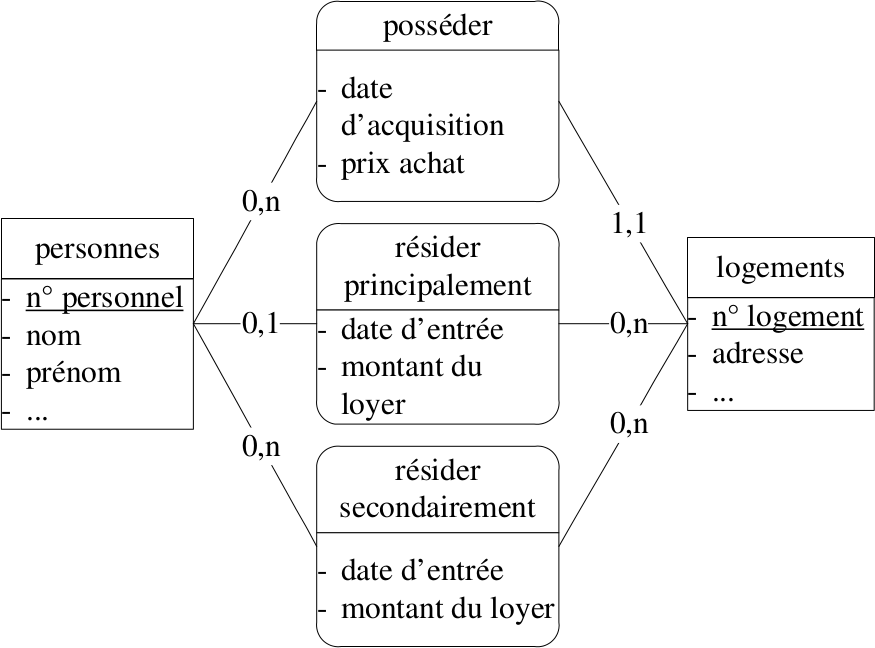
Associations plurielles
Deux même entités peuvent être plusieurs fois en association.
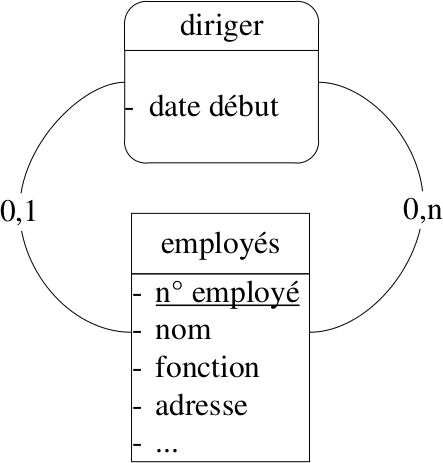
Association réflexive
Association d'une entité avec elle-même.
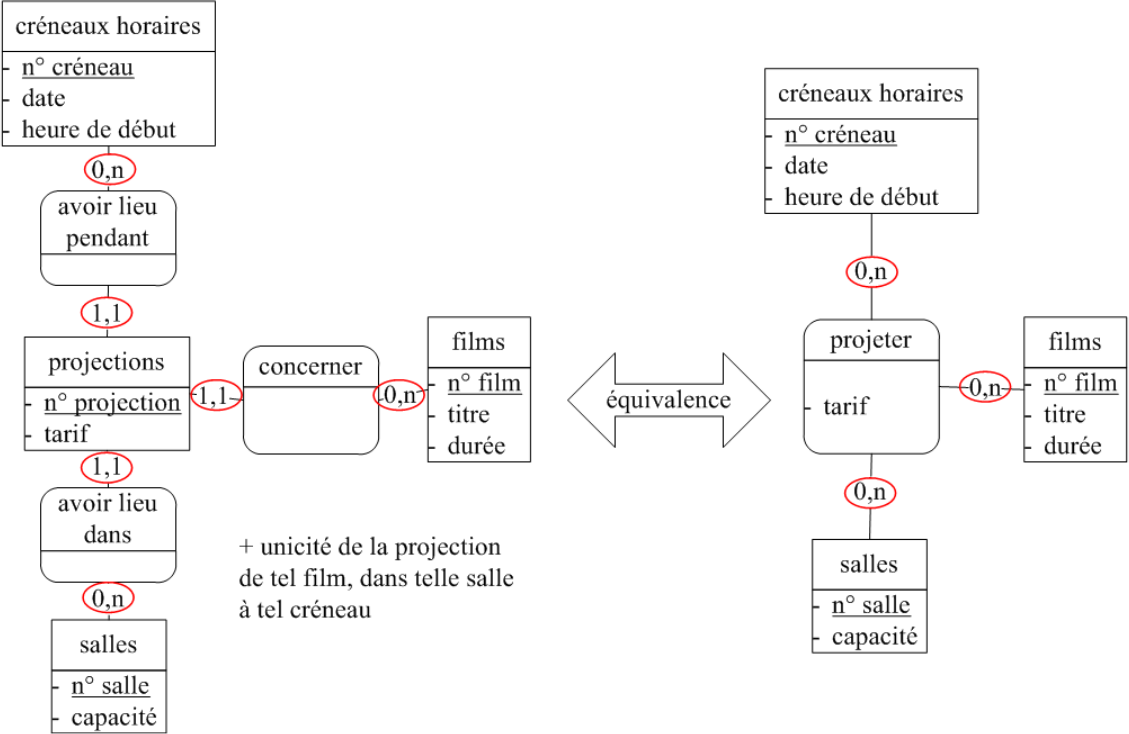
Associations n-aires
Une entité en relation 1,1 avec k autres où k ≥ 2 est susceptible d'être remplacée par une association d'arité k.
Règles de normalisation
Normalisation des entités
Toute entité remplaçable par une association doit être remplacée.
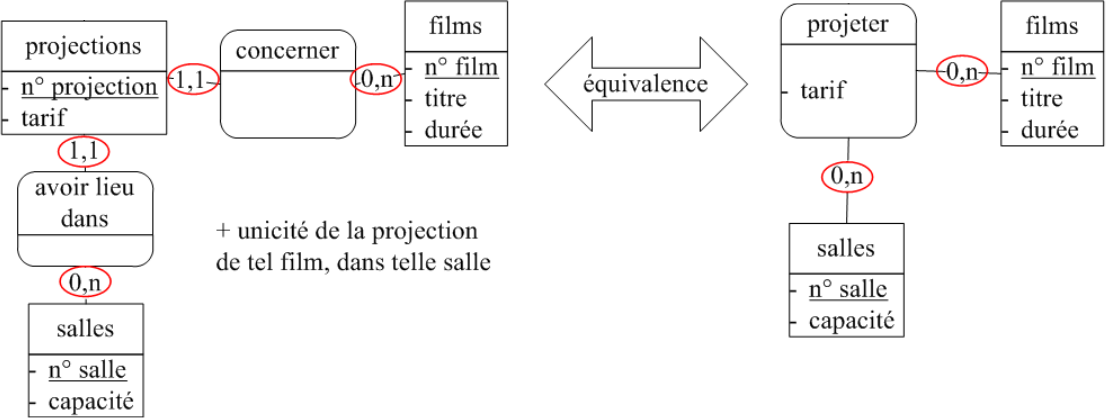
Normalisation des noms
Un nom d'entité, d'association ou d'attribut doit être unique.
Conseils :
- pour les entités, utiliser un nom commun au pluriel
exemples : clients, articles ; - pour les associations, utiliser un verbe à l'infinitif
exemples : effectuer, concerner ; - pour les attributs, utiliser un nom commun singulier
exemples : nom, numéro, libellé, description.
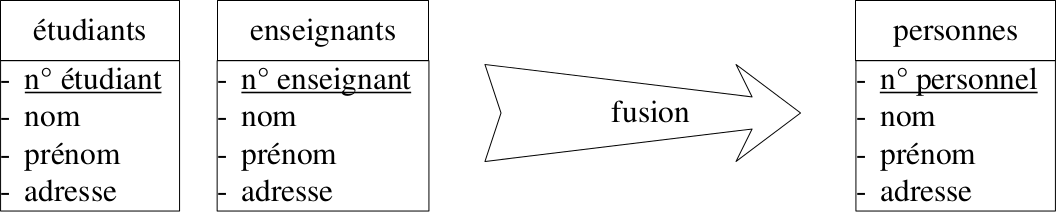
Normalisation des identifiants
Chaque entité doit posséder un identifiant.
Conseils :
- éviter les identifiants composés de plusieurs attributs ;
- préférer un identifiant court pour accélérer la recherche ;
- éviter également les identifiants susceptibles de changer au cours du temps (p.ex. plaques d'immatriculation) ;
- souvent, un entier auto-incrémenté est le meilleur choix.
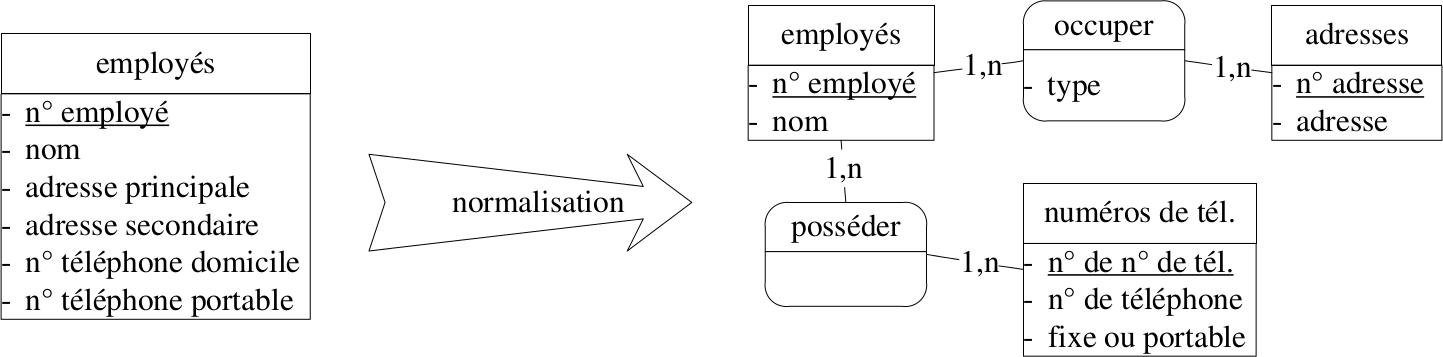
Normalisation des attributs
- Remplacer les attributs en plusieurs exemplaires par une association supplémentaire.
- Éviter l'ajout d'attributs calculables à partir d'autres attributs.
(Attributs calculables = prix totaux, moyennes...)
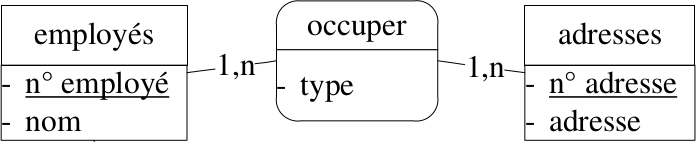
Normalisation des attributs des associations
Un attribut d'association dépend des identifiants de toutes les entités en relation.
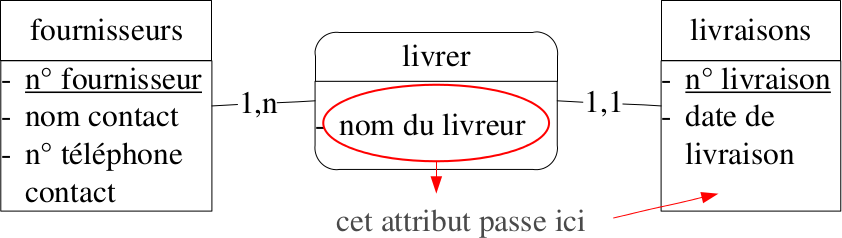
Normalisation des associations
...fantômes, redondantes ou en plusieurs exemplaires :
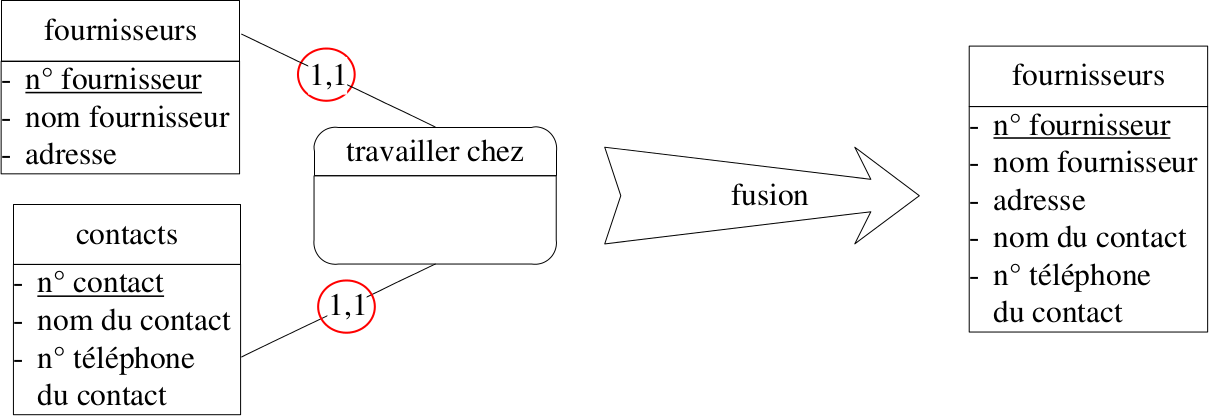

Normalisation des associations - suite
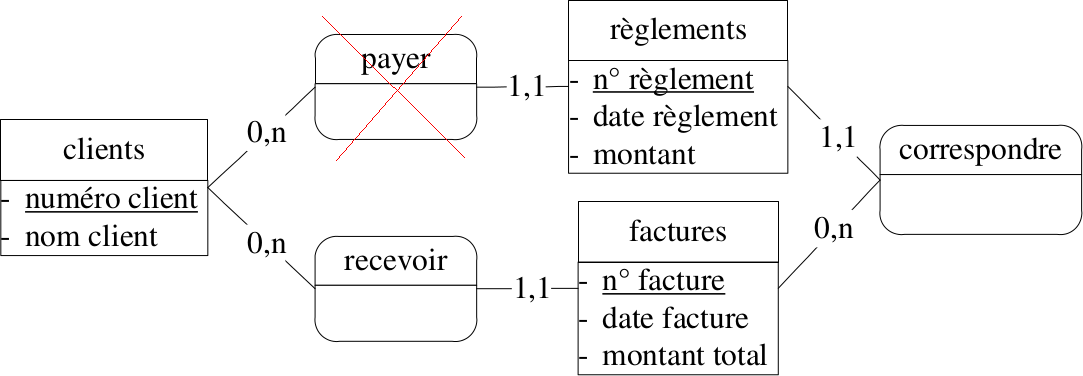
S'il existe deux chemins pour se rendre d'une entité à une autre, alors ils doivent avoir deux significations ou deux durées de vie différentes. Sinon on supprime le plus court.
Normalisation des cardinalités
- Une cardinalité minimale est toujours 0 ou 1.
- Une cardinalité maximale est toujours 1 ou n.
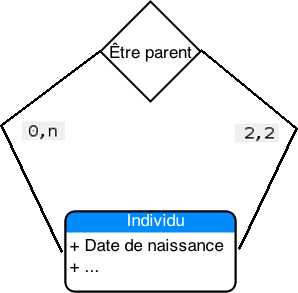
Exemple : relation de parenté "version généalogique"

Première forme normale (version E/A)
Les attributs prennent des valeurs atomiques.

Remarque : écrire les noms d'attributs au singulier aide à respecter cette règle
Seconde forme normale (v. E/A)
1NF et les attributs non identifiants de l'entité dépendent de l'identifiant en entier (éventuellement composé).
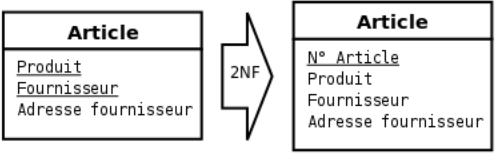
Troisième forme normale (v. E/A)
2NF et les attributs non identifiants d'une entité dépendent uniquement de l'identifiant (éventuellement composé).

Mnémotechnique : "The key, the whole key, nothing but the key" (Chris Date / Shakespeare)
Forme normale de Boyce-Codd (BCNF ; v. E/A)
3NF et aucun attribut de l'identifiant ne dépend d'un attribut non identifiant.
| Manager | Project | Branch |
|---|---|---|
| Brown | Mars | Chicago |
| Green | Jupiter | Birmingham |
| Green | Mars | Birmingham |
| Hoskins | Saturn | Birmingham |
| Hoskins | Venus | Birmingham |
- Manager → Branch — each manager works in a particular branch;
- Project,Branch → Manager — each project has several managers, and runs on several branches; however, a project has a unique manager for each branch.
Dépendances fonctionnelles (DF)
Définitions
Un attribut $Y$ dépend fonctionnellement d'un attribut $X$
$\Leftrightarrow$ une valeur de $X$ induit une
unique valeur de $Y$ : $X \rightarrow Y$
Ex. : si $X$ est le numéro d'un client et $Y$ son nom, alors $X \rightarrow Y$
Si $X$ = groupe d'attributs : DF non élémentaire.

Exercice : réexprimer les formes normales 2 et 3 en terme de DFs.
Définitions - DF (suite)
Relation : ensemble d'attributs formant une unité logique.
Exemple : R(numéro article, nom article, prix unitaire)
Soient $X$ et $Y$ deux ensembles d'attributs.
Dépendance fonctionnelle totale (DFT) $\Leftrightarrow \forall X' \subset X, X' \nrightarrow Y$
Clé minimale (ou irréductible) :
$X$ est une clé minimale de $R$ ssi. $\forall X' \subset X$, $X'$ n'est pas une clé
Exercice : exprimer "X,Y est une clé minimale de R(X,Y,Z,W)" à l'aide de connecteurs logiques
$(X,Y \rightarrow Z,W) \land \lnot (X \rightarrow Y,Z,W) \land \lnot (Y \rightarrow X,Z,W)$
Propriétés (axiomes d'Amstrong)
Soient X, Y, Z, W des ensembles d'attributs (entités diverses)
| Réflexivité | $Y \subseteq X \Rightarrow X \rightarrow Y$ |
| Augmentation | $X \rightarrow Y \land W \subseteq Z \Rightarrow X,Z \rightarrow Y,W$ |
| Transitivité | $X \rightarrow Y \land Y \rightarrow Z \Rightarrow X \rightarrow Z$ |
| Pseudo-transitivité | $X \rightarrow Y \land Y,Z \rightarrow W \Rightarrow X,Z \rightarrow W$ |
| Union | $X \rightarrow Y \land X \rightarrow Z \Rightarrow X \rightarrow Y,Z$ |
| Décomposition | $X \rightarrow Y,Z \Rightarrow X \rightarrow Y \land X \rightarrow Z$ |
Définitions - DF (suite)
Soient $R(X_1,...,X_n)$ une relation et $\mathcal{D}$ un ensemble de DF sur R.
Une dépendance fonctionnelle de $\mathcal{D}$ est dite canonique si son terme de droite ne contient qu'un attribut. Par exemple $A \rightarrow B$.
Fermeture transitive $\mathcal{F}(R)$ = ensemble des dépendances fonctionnelles
engendrées par $\mathcal{D}$ (notation non standard).
On note $\mathcal{D}^+$ la fermeture obtenue à partir de $\mathcal{D}$
Couverture minimale $\mathcal{C}(R)$ = ensemble de DF canoniques sur R permettant de reconstruire $\mathcal{D}^+$ par fermeture transitive, et telle qu'aucune de ses DF ne soit redondante ($\forall f \in \mathcal{C}, (\mathcal{C} \backslash f)^+ \neq \mathcal{D}^+$)
Exemple : $R(A,B,C,D), \mathcal{D} = \{A,B \rightarrow C, C \rightarrow D\}$
Fermeture transitive = $\{A,B \rightarrow C,D ; C \rightarrow D\}$
Couverture minimale = $\mathcal{D}$
Définition - graphe
Graphe de couverture minimale : graphe orienté dont les noeuds représentent des attributs (atomiques), et les arêtes des dépendances fonctionnelles directes (non transitives).
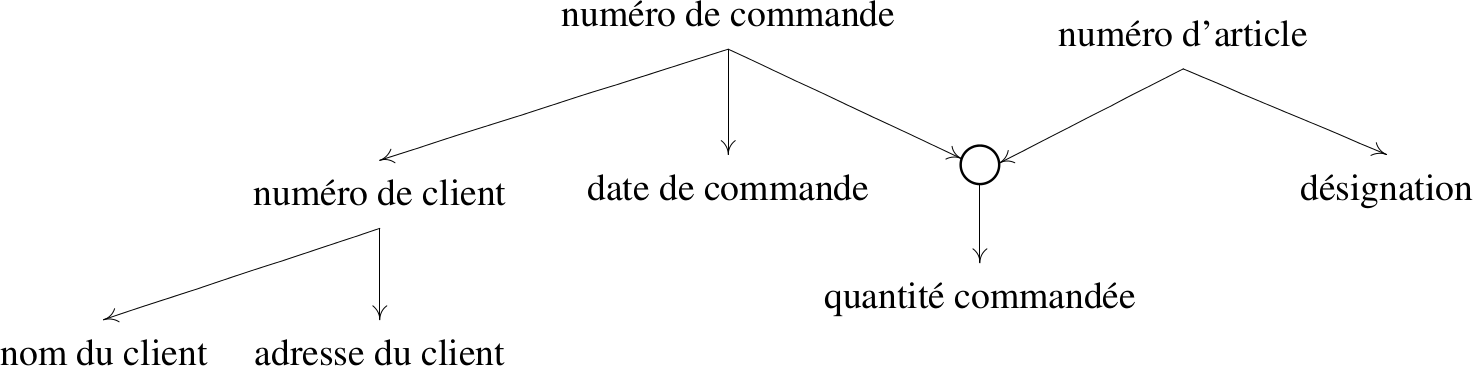
Traduction vers un schéma entités-associations
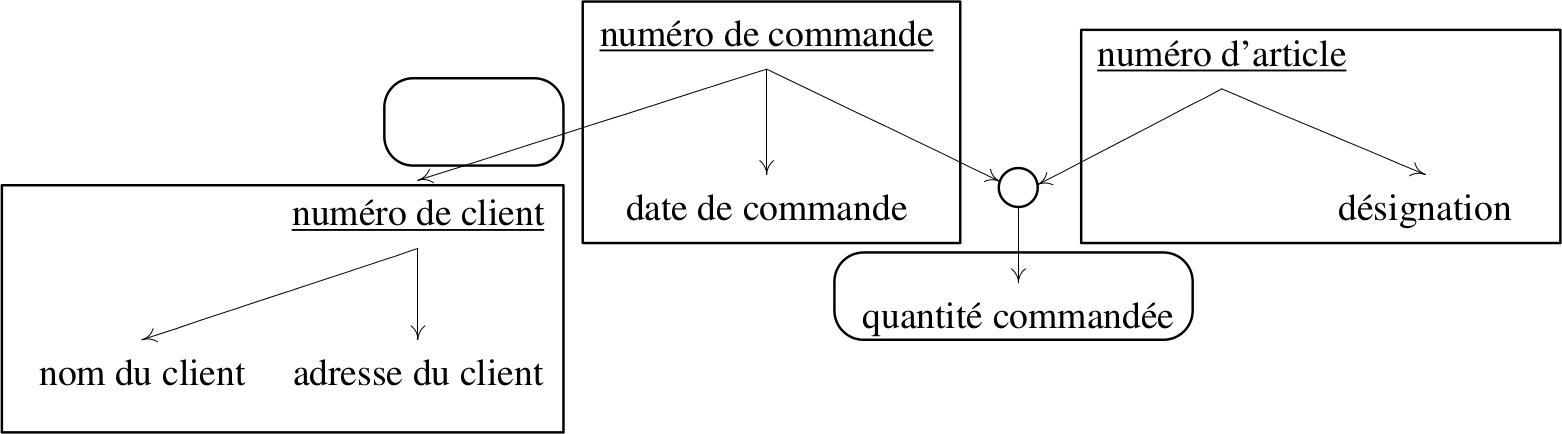
Remarque :
En réalité il faut déjà connaître les entités en présence pour établir correctement le graphe de
couverture minimale, ne serait-ce que pour y faire figurer leurs identifiants.
Donc cette technique est surtout une aide pour établir les associations entre les entités et pour
normaliser les entités et leurs associations.
Suggestion d'étapes pour obtenir un schéma E/A
- Repérer et souligner les identifiants
- Tous les attributs non identifiants qui dépendent directement d'un unique identifiant forment une entité
- Les dépendances élémentaires entre identifiants forment des associations binaires dont les cardinalités maximales sont 1 au départ de la dépendance fonctionnelle et n à l'arrivée
- ...Sauf si entre deux identifiants se trouvent deux dépendances élémentaires réflexives, auquel cas l'association binaire a deux card. max. valant 1
- Les attributs qui dépendent de plusieurs identifiants sont les attributs d'une association supplémentaire, dont les cardinalités maximales sont toutes n
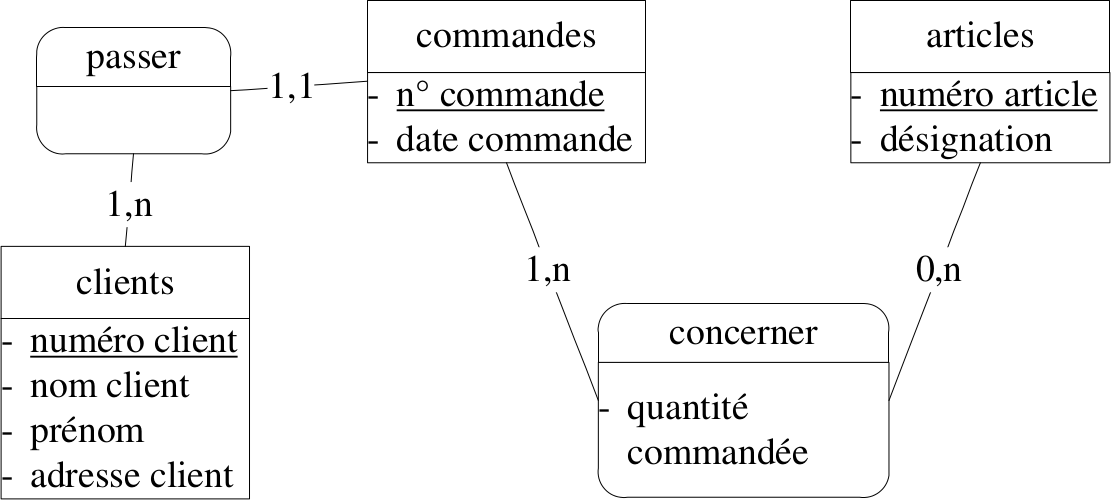
Résultat de la traduction (exemple)
Méthodologie de base - suggestion 1
- Identifier les entités en présence.
- Lister leurs attributs.
- Ajouter les identifiants (numéro arbitraire et auto-incrémenté).
- Établir les associations binaires entre les entités.
- Lister leurs attributs.
- Calculer les cardinalités.
- Vérifier les règles de normalisation et en particulier, la normalisation des entités (c'est à ce stade qu'apparaissent les associations non binaires), des associations et de leurs attributs ainsi que la troisième forme normale de Boyce-Codd.
- Effectuer les corrections nécessaires.
Méthodologie de base - suggestion 2
- Identifier les entités en présence et leur donner un identifiant (numéro arbitraire et auto-incrémenté).
- Ajouter l'ensemble des attributs et leur dépendances fonctionnelles directes avec les identifiants (en commençant par les dépendances élémentaires).
- Traduire le graphe de couverture minimale obtenu en un schéma entités-associations.
- Ajuster les cardinalités minimales.
- À ce stade, la majorité des règles de normalisation devraient être vérifiées. Il reste tout de même la normalisation des noms, la présence d'attributs en plusieurs exemplaires et d'associations redondantes ou en plusieurs exemplaires, à corriger.
Bilan
La conception d'une base de données peut démarrer par l'élaboration d'un schéma entités-associations.
Ce schéma doit respecter un certain nombre de règles pour éviter la redondances de données et permettre des évolutions sans repenser toute la structure, facilitant ainsi la maintenance de la base.
Des extensions existent pour mieux modéliser certaines situations :
- Agrégation : liens direct associations-associations.
- Identifiant relatif ou lien identifiant.
- Héritage : factorise les attributs communs.
L'étape suivante consiste à traduire un schéma E/A en un schéma intermédiaire (modèle logique) puis à l'implémenter dans un SGBD comme PostGreSQL (modèle physique).