Idée générale
Approximer une sortie $y$ par une combinaison linéaire des variables d'entrée $x_1, \dots, x_m$.
Exemple avec $m = 3$ :
$y = 2 x_1 - x_2 + 1.5 x_3$
Avec peut-être,
- $y$ = vitesse du vent aujourd'hui
- $x_1$ = vitesse du vent hier
- $x_2$ = vitesse du vent avant-hier
- $x_3$ = écart de pression hier/aujourd'hui
Régression affine simple (dimension 1)
$y = a_0 + a x$
> library(car)
> m = lm(prestige ~ education, data=Prestige)
> m$coefficients
(Intercept) education
-10.731982 5.360878
> Prestige[sample(1:nrow(Prestige), 5), c(1, 4)]
education prestige
plumbers 8.33 42.9
sales.clerks 10.05 26.5
office.clerks 11.00 35.6
psychologists 14.36 74.9
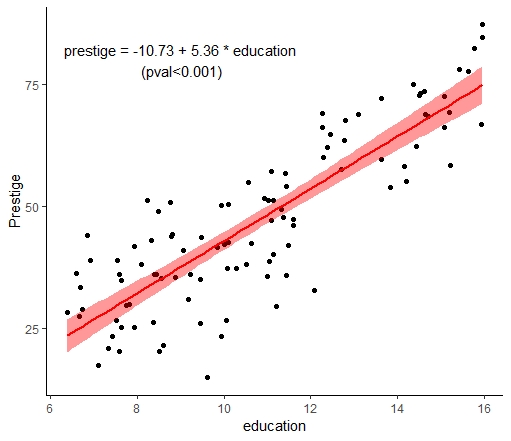
civil.engineers 14.52 73.1prestige $\simeq 5$ education $- 10$
Visualisation
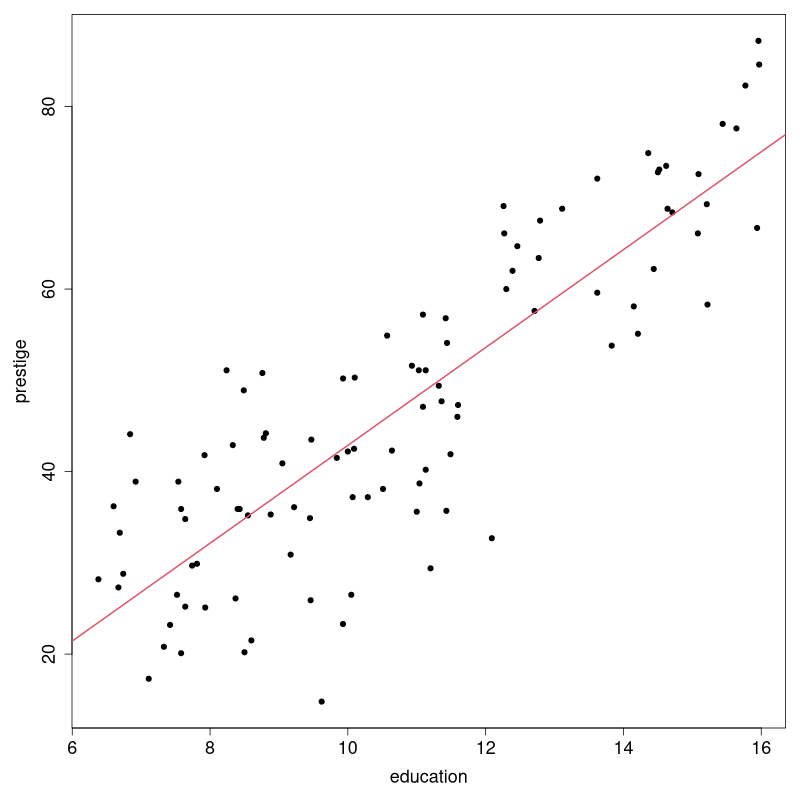
Qualité du modèle :
"(Adjusted) R-squared"
$\simeq 1 -$ erreur relative
> summary(m)
(...)
Multiple R-squared: 0.7228,
Adjusted R-squared: 0.72
# Calcul manuel :
> r <- z$residuals
> f <- m$fitted.values
> mss <- sum((f - mean(f))^2)
> rss <- sum(r^2)
> r2 <- mss / (mss + rss)Régression affine multiple
$y = a_0 + a_1 x_1 + a_2 x_2 + \dots + a_m x_m$
> library(car)
> m = lm(prestige ~ education+income+women, data=Prestige)
> m$coefficients
(Intercept) education income women
-6.794334203 4.186637275 0.001313560 -0.008905157> Prestige[indices,1:4]
education income women prestige
mining.engineers 14.64 11023 0.94 68.8
psychologists 14.36 7405 48.28 74.9
nurses 12.46 4614 96.12 64.7
sales.supervisors 9.84 7482 17.04 41.5
# ...On comprend mieux ! (Année 1971)Qualité $\simeq 0.79$ : peu d'amélioration.
Visualisation / plot(Prestige[,1:4)]
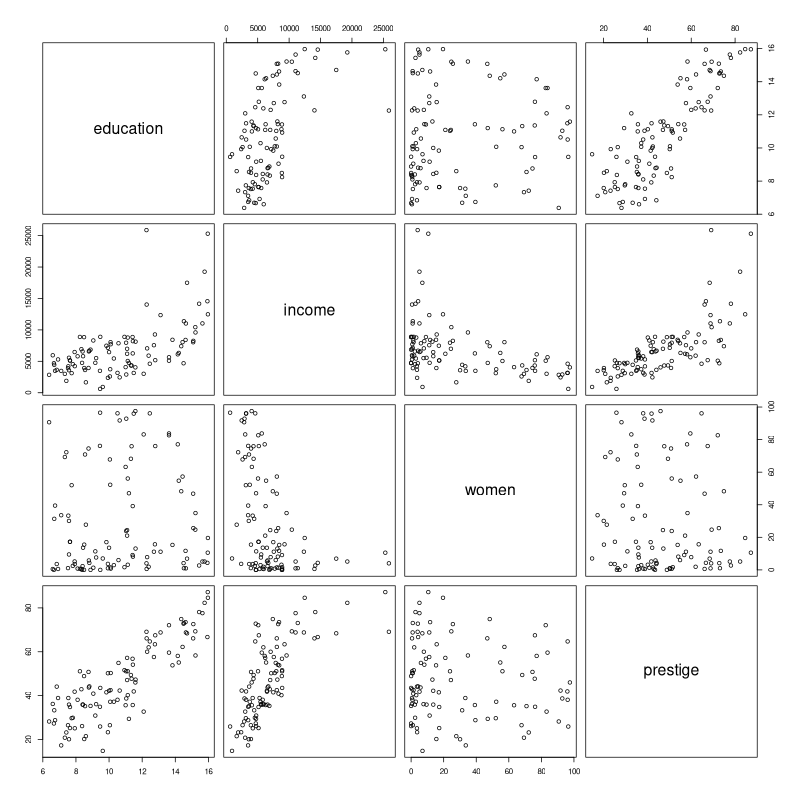
Problème potentiel
> d = data.frame(
x1 = c(1.01, 1),
x2 = c(1, 1.01),
y = c(0, 1))
> d
x1 x2 y
1.01 1.00 0
1.00 1.01 1
# Régression affine
> lm(y ~ ., d)
Coefficients:
(Intercept) x1 x2
101 -100 NA
# Régression linéaire
> lm(y ~ . - 1, d)
Coefficients:
x1 x2
-49.75 50.25Pénalisation
Idée = forcer les coefficients à ne pas prendre de grandes valeurs. Minimiser...
- erreur + $\lambda \sum_{i=1}^{m} |a_i|^2$ = régression ridge.
- erreur + $\lambda \sum_{i=1}^{m} |a_i|$ = régression LASSO.
> library(glmnet)
# Ridge:
> g = glmnet(d[,1:2], d[,3], alpha=0, lambda=10)
> c(g$a0, as.numeric(g$beta))
0.500000 -4.545455 4.545455
# LASSO:
> g = glmnet(d[,1:2], d[,3], alpha=1, lambda=1)
> c(g$a0, as.numeric(g$beta))
0.5 0.0 0.0Ridge & LASSO en images
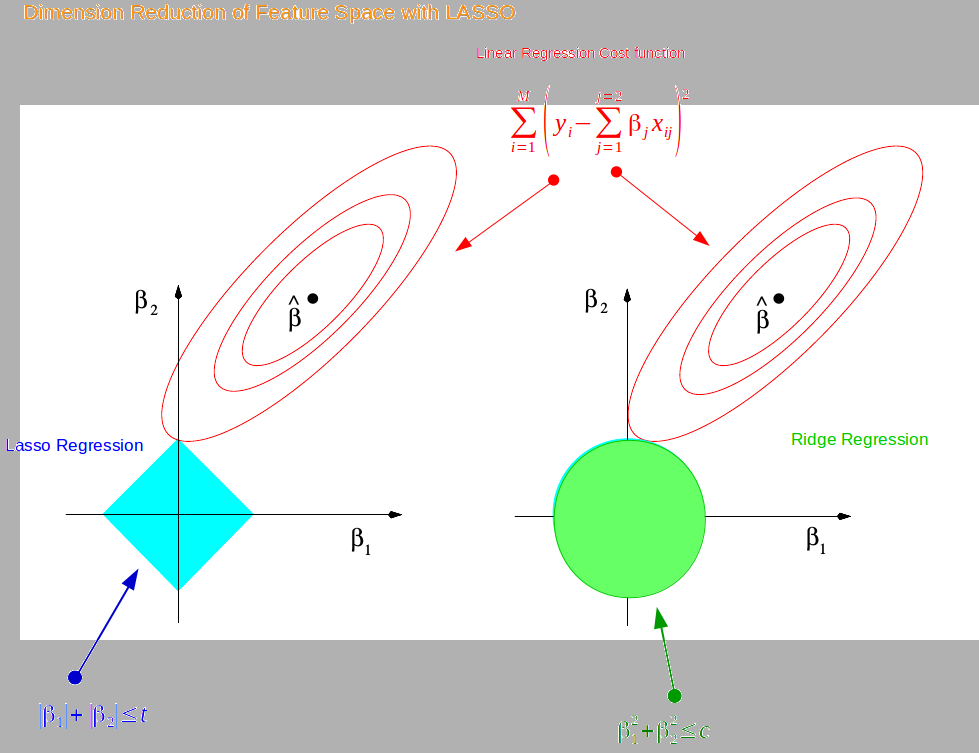
[Hors "programme" :] Présentation Ridge + LASSO
Prédiction
> library(glmnet)
> d = read.csv("https://archive.ics.uci.edu/ml/machine-learning-databases/communities/communities.data", header=F, na.strings="?")
> d = d[,-4]
> indices = which(apply(d, 1, function(r) all(!is.na(r))))
> d = d[indices,]
> dim(d)
123 127 #plus de colonnes que de lignes> m0 = lm(V128 ~ ., d)
# Des warnings, fit parfait : normal
> x = as.matrix(d[,-127])
> y = as.matrix(d[,127])
> m1 = cv.glmnet(x, y, alpha=1) #LASSO
> p1 = predict(m1, x, s=m1$lambda.min)
> rss = sum( (p1 - y)^2 )
> mss = sum( (p1 - mean(p1))^2 )
> mss / (rss + mss)
0.87 #pas mal, et...sum(m1$glmnet.fit$beta[,m1$index[1]] != 0.0)
# Seulement 27 coefficients non nuls !Recette
Si relativement peu de variables :
régression linéaire (multiple).
Si warnings, considérer régression ridge.
Si (relativement) beaucoup de variables :
régression LASSO.
Généralisations
Idée 1 : fabriquer une nouvelle variable.
> library(glmnet)
# "Indice d'obésité" en fonction de taille/poids
> d = read.csv("https://raw.githubusercontent.com/chriswmann/datasets/master/500_Person_Gender_Height_Weight_Index.csv")
> m0 = lm(Index ~ Height+Weight, d)
R2 = 0.83 #pas mal, mais...# Ajout logique de l'IMC
> d['BMI'] = d['Weight'] / (d['Height']/100)^2
> m0 = lm(Index ~ Height+Weight+BMI, d)
R2 = 0.87 #un peu mieuxIdée 1 bis : régression polynomiale.
$$y = a_0 + a_1 x + a_2 x^2 + \dots + a_d x^d$$
Idée 2 : fonctions non linéaires = GAM
$$y = a_0 + f_1(x_1) + f_2(x_2) + \dots + f_m(x_m)$$
Idée 3 : généralisation de GAM = PPR
$$y = a_0 + f_1(\beta_1 x) + f_2(\beta_2 x) + \dots + f_d(\beta_d x)$$
Utilisation en R
> library(mgcv)
> gam(Petal.Length ~ s(Sepal.Width) +
s(Sepal.Length) +
s(Petal.Width),
data=iris)
> ppr(Petal.Length ~ ., iris, nterms=5)Essayer les fonctions summary(), plot() ...
Complément : optimisation PPR
$$\arg\min_{\beta, f} \sum_{i=1}^{n} \left[ y_i - \sum_{j=1}^{r} f_j(\beta_j x_i) \right]^2$$ $\rightarrow$ Impossible, donc on optimise "pas à pas" :
- Trouver $\beta_1, f_1$ minimisant $\sum_{i=1}^{n} [y_i - f_1(\beta_1 x_i)]^2$
- Noter $r_i = y_i - f_1(\beta_1 x_i)$ les résidus, et
trouver $\beta_2, f_2$ minimisant $\sum_{i=1}^{n} [r_i - f_2(\beta_2 x_i)]^2$ - ...etc (jusqu'à avoir $r$ termes).
Exercice 1
Cherchez à prédire le nombre de personnes au chômage (variable 'unemploy') en fonction des autres, avec le jeu de données economics .
Vous pouvez éventuellement vous inspirer de / comparer avec cette page.
Exercice 2
Cherchez à prédire...
- la variable 'Volume' du dataset 'trees'
- la variable 'Employed' du dataset 'longley'
Les deux sont dans le package 'datasets' :
library(datasets)
data(trees)
data(longley)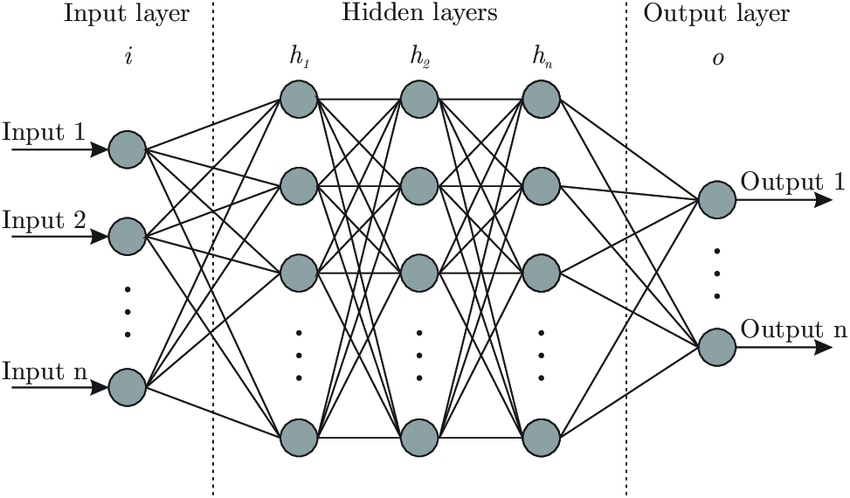
Neurone formel (ou artificiel)
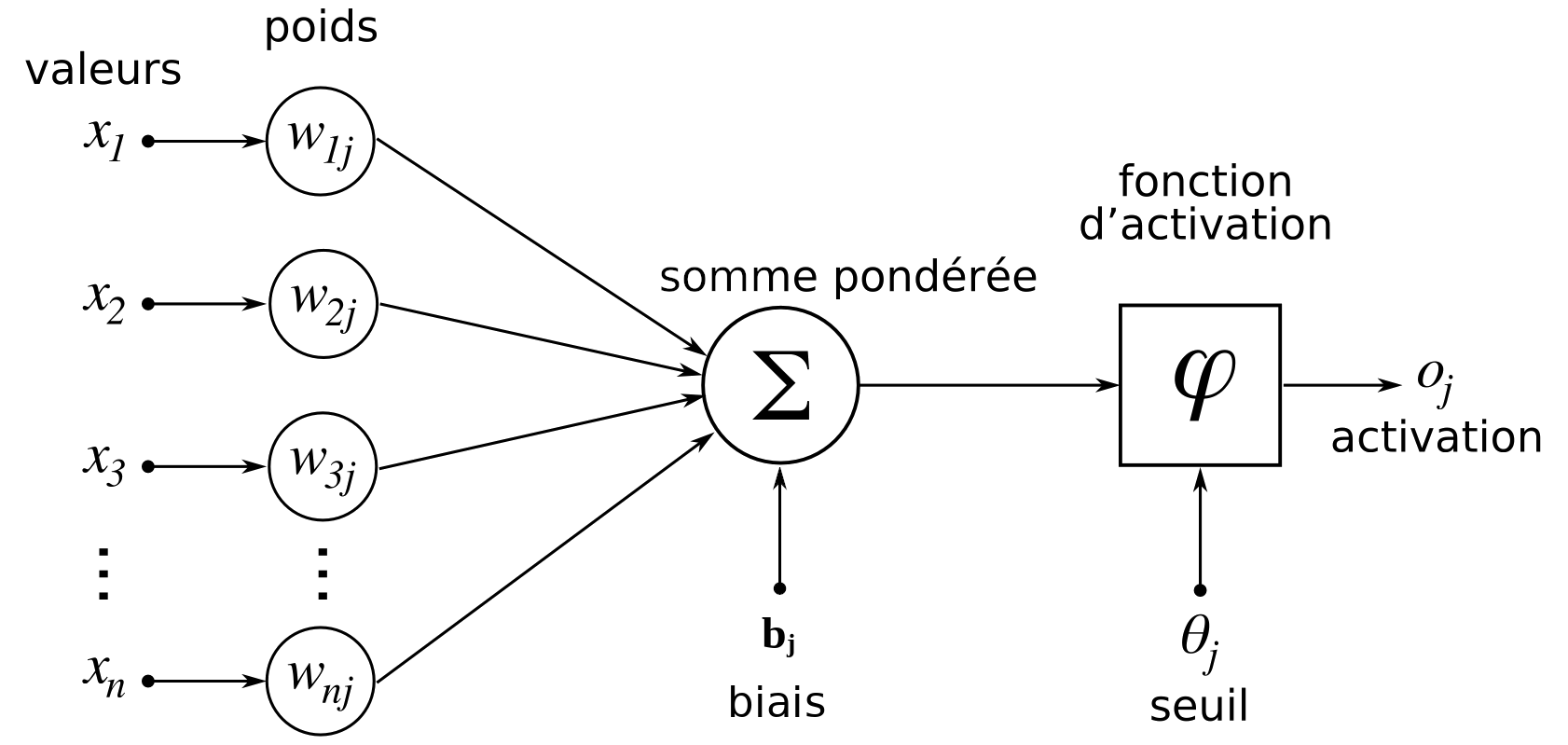
$o_j = \varphi \left( b_j + \sum_{i=1}^{n} w_{ij} x_i \right)$
Fonction d'activation
$\varphi: \mathbb{R} \rightarrow \mathbb{R}$, souvent croissante (voire bornée)
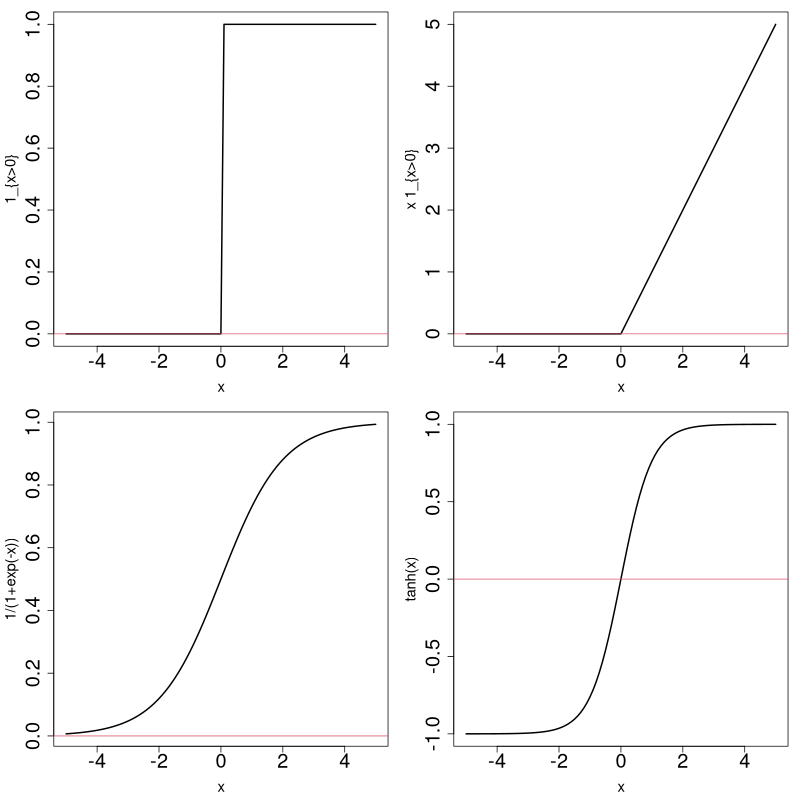
Une fonction adaptée à un type de problème...
Régression
library(neuralnet)
vec_11 = rep(c(-1,1),each=5)
df = data.frame(x=vec_11, y=vec_11)
nn = neuralnet(y ~ ., df,
linear.output=TRUE, #pas de transformation en sortie
act.fct = function(x) x, #activation = identité
hidden=0) #...cf suite du cours :-)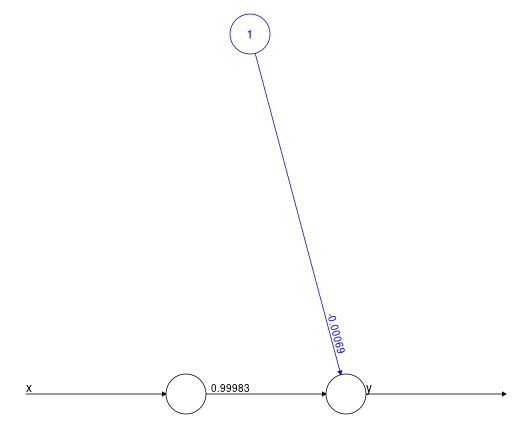
= (très) Simple
régression linéaire
Exemple plus complexe
library(car)
nn = neuralnet(prestige ~ education+income+women, Prestige,
linear.output=TRUE, act.fct = function(x) x, hidden=0)
plot(nn)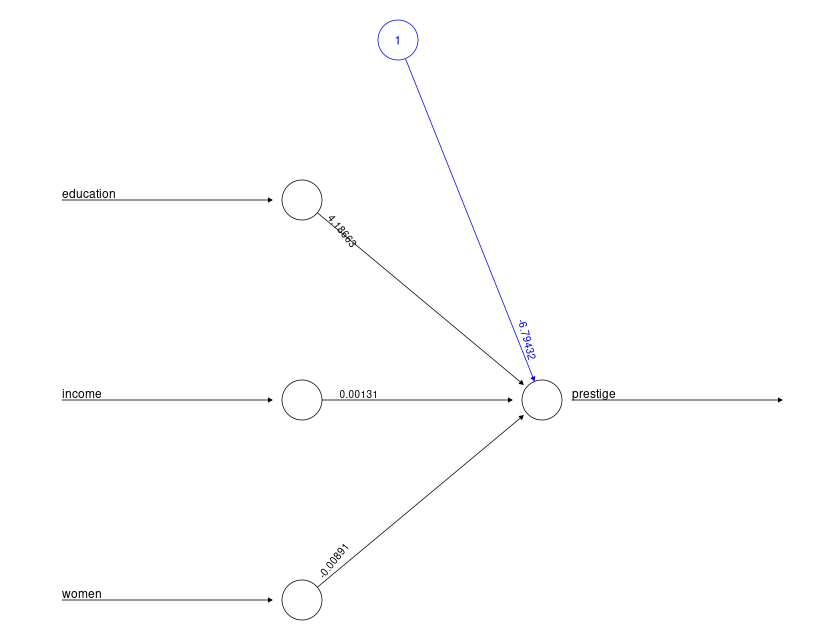
On retrouve les résultats précédents (fonction lm...)
Apprentissage
Illustration sur un exemple simple, lui-même issu du livre "Réseaux neuronaux" de Jean-Philippe Rennard.
Objectif = reconnaître un motif précis sur un carré de 4 pixels noirs ou blancs.

Mise à jour des poids
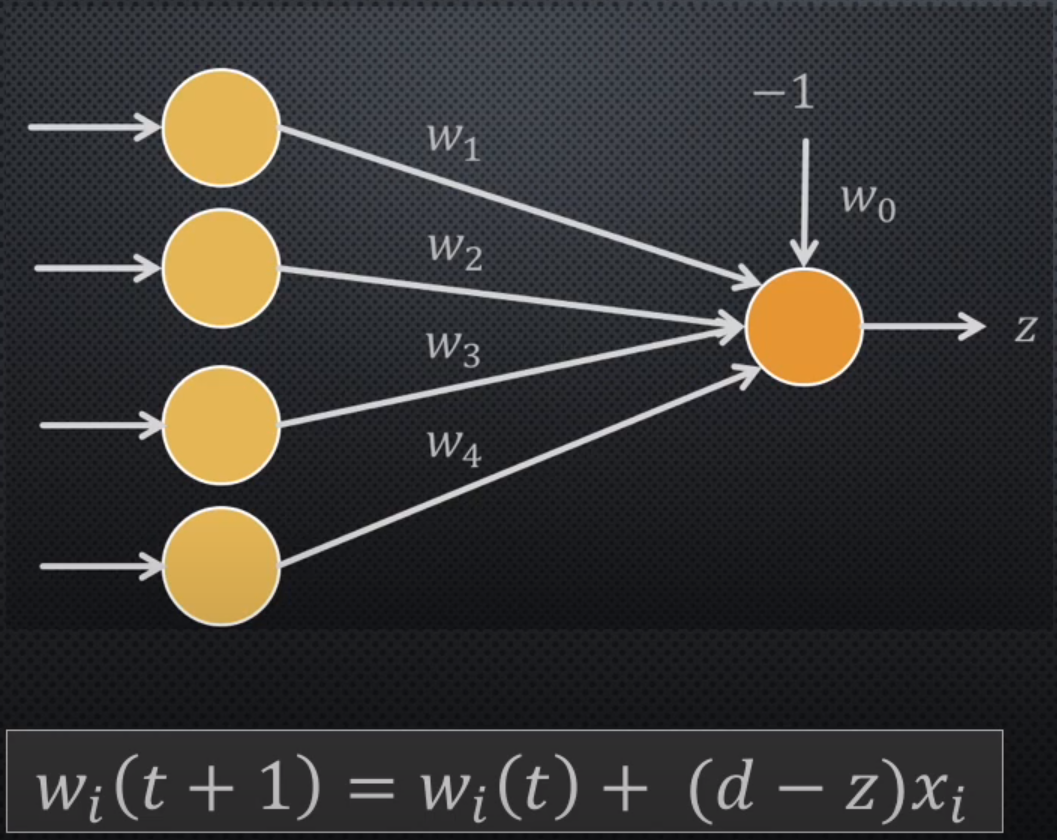
Itérations (activation = Heaviside)
- $w_1 = \dots = w_4 = 0, w_0 = 2$ (exemple 1001)
- $w_1 = 1, w_2 = w_3 = 0, w_4 = 1, w_0 = 1$
(1001, ok) - $w_1 = 0, w_2 = w_3 = -1, w_4 = 0, w_0 = 2$
(1111, ok) - $w_1 = 1, w_2 = w_3 = -1, w_4 = w_0 = 1$
(1001, ok) - etc...
Question : toujours convergence ?
Linéairement séparable ?
Perceptron = (hyper)plan : au-dessus ou en dessous...
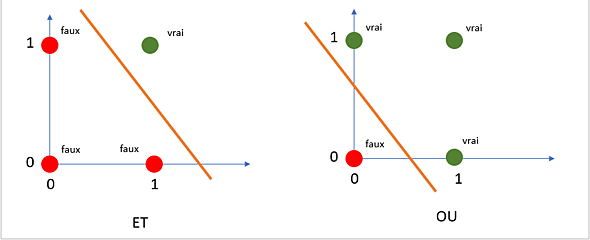
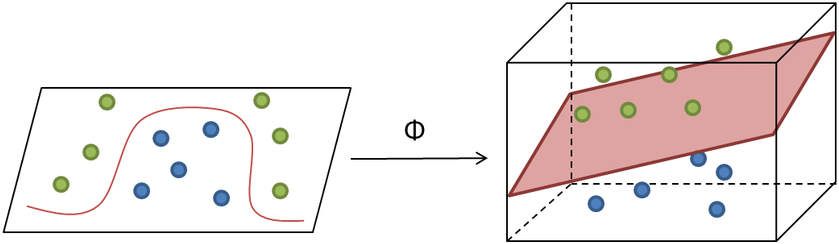
Esquisse code Scala
 Source
Source
Couches cachées
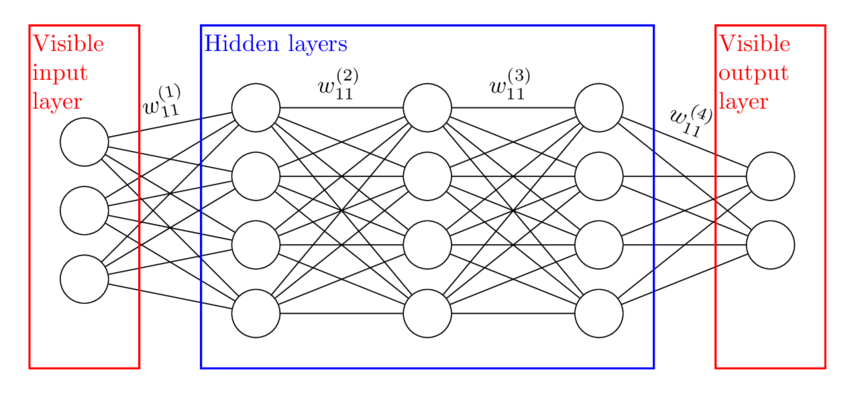
Exemple
softplus <- function(x) log(1 + exp(x))
nn <- neuralnet(
(Species == "setosa") ~ Petal.Length + Petal.Width,
iris, linear.output = FALSE,
hidden = c(3, 2), act.fct = softplus)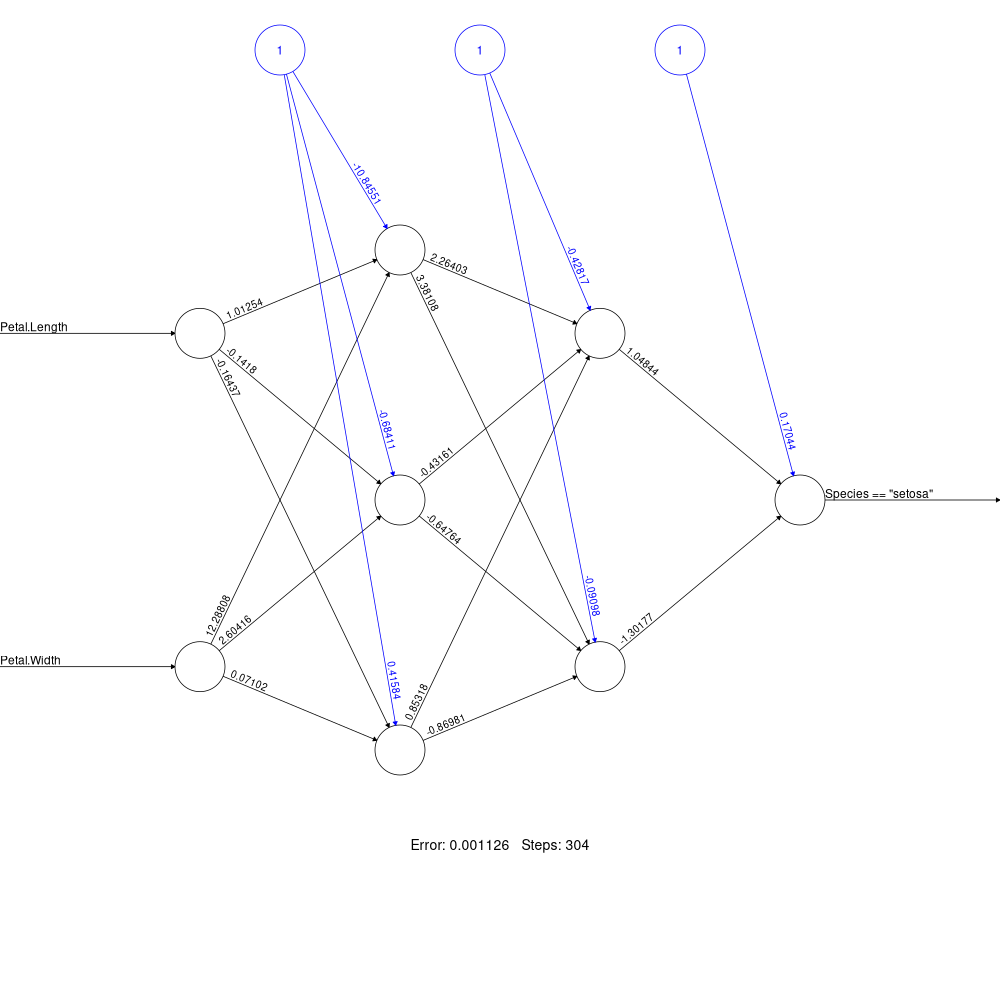
Quelques mots sur l'apprentissage
L'idée est d'évaluer l'impact d'une variation des poids sur l'erreur finale. Pour cela on calcule la dérivée de l'erreur en remontant petit à petit dans le réseau.
Voir la fin de cette présentation, et pour les calculs, la page Wikipedia par exemple.
Illustration : XOR
> X = np.array([[0,0],[0,1],[1,0],[1,1]])
> y = np.array([0, 1, 1, 0])
> nn = neural_network.MLPClassifier(
hidden_layer_sizes=(3,), max_iter=2000)
> clf = nn.fit(X, y)
> clf.predict(X)
array([0, 0, 1, 0])
> nn = neural_network.MLPClassifier(
hidden_layer_sizes=(6,), max_iter=2000)
> clf = nn.fit(X, y)
> clf.predict(X)
array([0, 1, 1, 0])
# clf.coefs_
# clf.intercepts_Illustration MNIST
Comparaison avec PPR
PPR : une seule couche cachée, addition en sortie (pas de transformation). Fonctions d'activations adaptées aux données.
MLP : $n$ couches cachées, transformation en sortie. Fonctions d'activations fixées.
$\rightarrow$ Ce dernier point permet plus de parallélisme dans l'apprentissage des MLP versus PPR...
Exercice
Lisez cet article puis implémentez la méthode.
Variantes
- RPSLS (+ Lizard + Spock).
- Considérer un match nul comme une défaite.
Essayez aussi de faire jouer cet algorithme contre ceux du TP "Chaînes de Markov".
Pour approfondir un peu
Un cours chouette.Voir aussi l'aide scikit-learn et l'aide tensorflow.