$k$ plus proches voisins

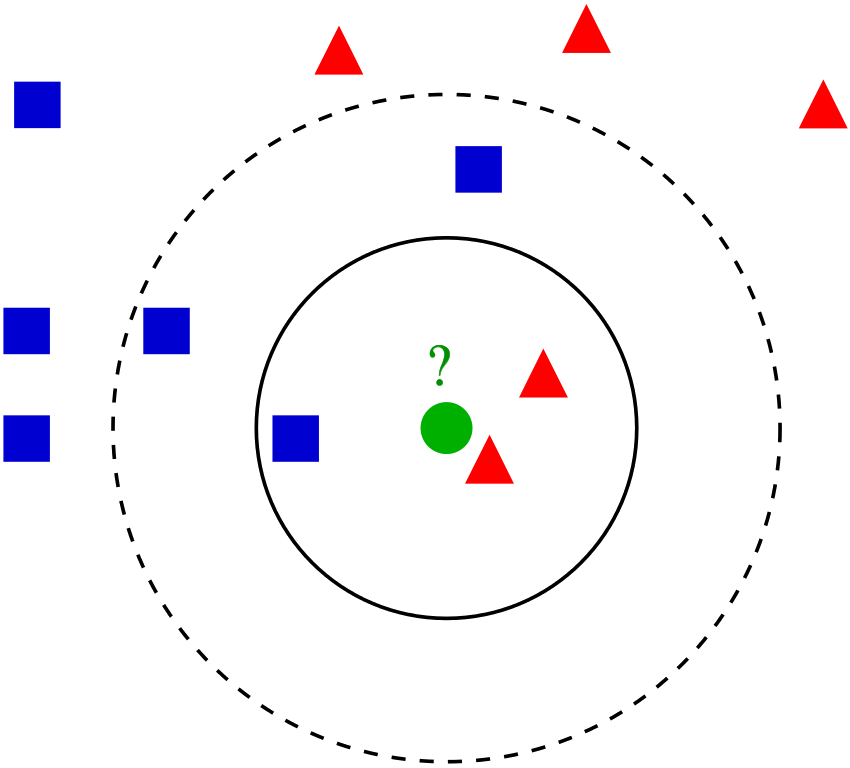
Idée

Un individu devrait ressembler à ses "voisins".

On peut alors prédire...

  • sa classe (exemple : pluie) en regardant celles de ses voisins,
  • sa valeur (exemple : température) en regardant celles de ses voisins.

Exemple 1

Ciblage publicitaire : montrer au client $X$ des publicités ayant fonctionné sur ses voisins.

Questions :

  • quelle distance inter-profils ?
  • combien de voisins ?

Exemple 2

Une banque dispose de profils de clients détenteurs d'une carte de crédit :

  • âge,
  • nombre de personnes à charge,
  • ancienneté,
  • nombre de produits bancaires, etc

Qui risque de mettre fin à son contrat ?

Méthode (naïve)

Chaque jour,

  1. comparer les profils clients actifs à ceux ayant clôturé leur compte à $J-x$
  2. contacter ceux dont les "voisins" sont plutôt des comptes fermés,

en supposant une actualisation journalière de la BD

Avec Python

# Chargement du jeu de données (ou pandas.read_csv(...))
iris = sklearn.datasets.load_iris()

# Définition du modèle : vote majoritaire
# parmi les 15 plus proches voisins.
model = sklearn.neighbors.KNeighborsClassifier(n_neighbors=15)

# "Entraînement" du modèle :
fitted = model.fit(iris["data"], iris["target"])

# Évaluation de l'erreur (sur l'ensemble d'apprentissage)
predictions = fitted.predict(iris["data"])
erreurs = sum(predictions != iris["target"]) #2

Problèmes :

  • prédiction sur les données d'entraînement ?
  • nombre de voisins = 15 ?

Séparation entraînement / test

Problème : plus proche voisin d'un point = lui-même
$\Rightarrow$ aucune erreur !

Solution : évaluer l'erreur sur un autre ensemble.

# Division en ensembles d'apprentissage / test
X_train, X_test, y_train, y_test =
  sklearn.model_selection.train_test_split(
    iris["data"], iris["target"], test_size=0.3)

# "Entraînement" :
fitted = model.fit(X_train, y_train)

# Évaluation de l'erreur sur l'ensemble de test :
predictions = fitted.predict(X_test)
erreurs = sum(predictions != y_test)

Évaluation de l'erreur

L'ensemble de test peut être (par chance)

  • très facile à prédire, ou
  • très difficile à prédire.

Idée : recommencer $V$ fois, $V \gtrsim 10$

> param_grid = {'n_neighbors':[7, 9, 11, 13, 15, 19, 23]}
> splits = sklearn.model_selection.ShuffleSplit(
    n_splits=10, test_size=0.4)
> scv = sklearn.model_selection.GridSearchCV(
    sklearn.neighbors.KNeighborsClassifier(),
    param_grid, cv=splits, scoring="accuracy")
> c = scv.fit(iris["data"], iris["target"])
> print(c.best_params_)
{'n_neighbors': 11}

Alternative

Certains individus peuvent être prédits plusieurs fois, et d'autres jamais. Exemple :

Train        Test
[1, 2, 3, 4] [5, 6]
[1, 3, 4, 6] [2, 5]
[2, 4, 5, 6] [1, 3]

L'individu 4 n'est jamais prédit, 5 l'est deux fois.

Solution :

  1. partition en $k$ parties de taille $n / k$
  2. pour $i$ allant de 1 à $k$ :
    • test sur le bloc $i$,
    • entraînement sur les $k-1$ autres

Illustration

> import numpy as np
> X = np.array([[0,0], [0,0], [0,0], [0,0]])
> y = np.array([0, 0, 0, 0])

> kf = sklearn.model_selection.ShuffleSplit(
    n_splits=2, test_size=0.5)
> for train_index, test_index in kf.split(X):
>   print("TRAIN:", train_index, "TEST:", test_index)
TRAIN: [2 1] TEST: [0 3]
TRAIN: [3 2] TEST: [0 1]

0 prédit deux fois, 2 jamais.

> kf = sklearn.model_selection.KFold(n_splits=2)
> for train_index, test_index in kf.split(X):
>   print("TRAIN:", train_index, "TEST:", test_index)
TRAIN: [2 3] TEST: [0 1]
TRAIN: [0 1] TEST: [2 3]

Chaque individu est prédit exactement une fois.

$k$-fold cross-validation

> splits = sklearn.model_selection.StratifiedKFold(
    n_splits=10, shuffle=True)
> scv = sklearn.model_selection.GridSearchCV(
    sklearn.neighbors.KNeighborsClassifier(),
    param_grid, cv=splits, scoring="accuracy")
> c = scv.fit(iris["data"], iris["target"])
> c.best_params_
{'n_neighbors': 11}

Les deux méthodes sont équivalentes ici.

...Ce n'est pas le cas en général !

> c.cv_results_['mean_test_score']
array([0.97, 0.97, 0.98, 0.97, 0.99, 0.98, 0.97])

Régression

Idée = remplacer vote majoritaire par moyenne

$\hat y = \frac{1}{k} \sum_{i=1}^{k} y_{n_i}$
avec $n_1, \dots, n_k$ indices des $k$ PPV. 

> diab = sklearn.datasets.load_diabetes()
> param_grid = {'n_neighbors':[3, 5, 7, 9, 11]}
> splits = sklearn.model_selection.LeaveOneOut()
> scv = sklearn.model_selection.GridSearchCV(
    sklearn.neighbors.KNeighborsRegressor(),
    param_grid, cv=splits, scoring="max_error")
> c = scv.fit(diab["data"], diab["target"])
> c.cv_results_['mean_test_score']
array([-49.2, -47.0, -45.9, -45.4, -46.3, -47.0, -47.7])
# ...Variabilité de l'erreur :
> 2 * c.cv_results_['std_test_score']
array([80.1, 71.9, 70.3, 68.2, 66.7, 66.1, 64.9])

Amélioration, extension

Moyenne pondérée :
$\hat y \propto \sum_{i=1}^{k} \frac{y_{n_i}}{\|x - x_{n_i}\|}$

Généralisation = noyau :
$\hat y \propto \sum_{i=1}^{n} K(\|x - x_i\|) y_i$

Exemple classique :
$K(z) = \exp\left(-\frac{z^2}{\sigma^2}\right)$
(noyau gaussien)

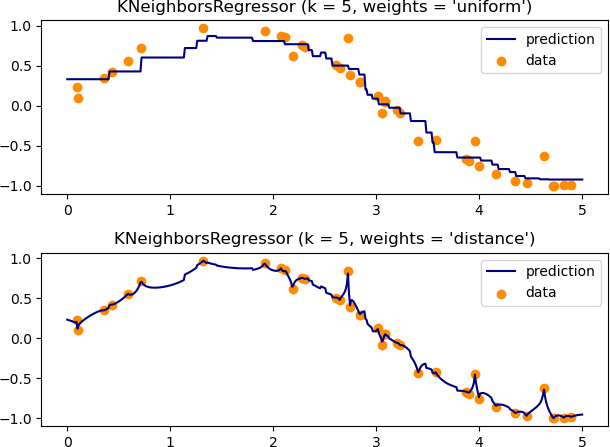
Avec Python

# Pondération par 1 / distance :
scv = sklearn.model_selection.GridSearchCV(
  sklearn.neighbors.KNeighborsRegressor(weights='distance'),
  param_grid, cv=splits, scoring="max_error")
# Noyau gaussien
def kernel(distances):
  h = 2 #à ajuster...
  weights = np.exp(-distances**2 / h)
  return weights
KNeighborsRegressor(n_neighbors=12, weights=kernel)

Exercice 0

Reprenez les données iris, et faites varier le nombre de voisins jusqu'à $n-1$. Tracez l'évolution de l'erreur. Expliquez.

Exercice 1

Prenez le temps de comprendre les principaux paramètres de make_regression. Utilisez alors cette fonction pour générer des jeux de données avec 500 lignes et un nombre croissant de colonnes. Comment évoluent les performances du modèle quand n_informative augmente ? Commentez.

Exercice 2

Récupérez les données "Pima Indians Diabetes", disponibles par exemple sur Kaggle.

  1. Effectuez une validation croisée sur une grille de paramètres d'abord grossière mais balayant beaucoup de valeurs, puis réduisez la.
  2. Changez les poids pour pondérer avec l'inverse de la distance. Amélioration ?
  3. Évaluez la corrélation entre chaque variable et la sortie, puis éliminez-en éventuellement certaines. Commentez.

Ébauche de corrigé

Petit complément

Reprenant ce qui a été dit dans le cours, en expliquant différemment :)

Exercices type examen

import random, math
import numpy as np
def getData(n, K, rs=None):
  x = random.sample(range(0, 10), n)
  y = random.sample(range(0, 10), n)
  classes = random.choices(range(1, K+1), k=n)
  return np.array([x, y]).T, classes
def getTest(n):
  return random.sample(range(1, n), math.floor(0.3*n))

Appelez "getData(10, 2)" (ou $K=3$), puis calculez le taux de bien classés sur deux ensembles d'entraînement ("getTest(10)").

Recommencez :)