
Motivations
Décrire l'évolution d'un système où l'état courant détermine les probabilités de se trouver dans un autre état après changement.
Exemples :
- Roulette ("pair" / "impair") au casino
- Marche aléatoire dans un labyrinthe
- Niveau dans un jeu vidéo simple (Tetris)
-
Niveau de pollution -
Performance au 400m
Introduction
Chaîne de Markov = états + transitions.
Exemple : état = progression dans un jeu
États = jouer au niveau 1, 2, contre le boss final (B)
avoir perdu (P)
avoir terminé le jeu (T)
- Transitions $1 \rightarrow 2, P$ ; $2 \rightarrow B, P$ ; $B \rightarrow P, T$
- États $P$ et $T$ terminaux (on y reste !)
Probabilités de transition ?
Matrice $P \Leftrightarrow$ graphe de transition
$$\begin{pmatrix} 0.0 & 0.7 & 0.0 & 0.3 & 0.0\\ 0.0 & 0.0 & 0.5 & 0.5 & 0.0\\ 0.0 & 0.0 & 0.0 & 0.8 & 0.2\\ 0.0 & 0.0 & 0.0 & 1.0 & 0.0\\ 0.0 & 0.0 & 0.0 & 0.0 & 1.0 \end{pmatrix}$$
import pydtmc as m
P = [
[0.0, 0.7, 0.0, 0.3, 0.0],
[0.0, 0.0, 0.5, 0.5, 0.0],
[0.0, 0.0, 0.0, 0.8, 0.2],
[0.0, 0.0, 0.0, 1.0, 0.0],
[0.0, 0.0, 0.0, 0.0, 1.0]]
mc = m.MarkovChain(P,
['1', '2', 'B', 'P', 'T'])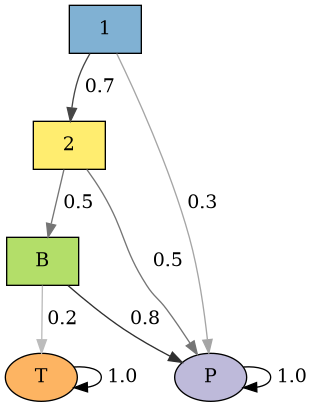
Découpage de $P$
$$\left[ \begin{array}{ccc|cc} \color{red}{0.0} & \color{red}{0.7} & \color{red}{0.0} & 0.3 & 0.0 \\ \color{red}{0.0} & \color{red}{0.0} & \color{red}{0.5} & 0.5 & 0.0 \\ \color{red}{0.0} & \color{red}{0.0} & \color{red}{0.0} & 0.8 & 0.2 \\ \hline 0.0 & 0.0 & 0.0 & 1.0 & 0.0 \\ 0.0 & 0.0 & 0.0 & 0.0 & 1.0 \end{array} \right]$$
États "transients" en haut à gauche: matrice $Q$.
États "absorbants" en bas à droite.
Matrice fondamentale
$$N = (I - Q)^{-1}$$
$N[i,j]$ = nombre de passages moyen par l'état $j$
si on commence en $i$
Sur l'exemple, [code: mc.fundamental_matrix]
$$N = \begin{pmatrix} 1 & 0.7 & 0.35 \\ 0 & 1.0 & 0.50 \\ 0 & 0.0 & 1.00 \end{pmatrix}$$
Calculs / en vert = matrice $R$.
$$\left[ \begin{array}{ccc|cc} 0.0 & 0.7 & 0.0 & \color{green}{0.3} & \color{green}{0.0} \\ 0.0 & 0.0 & 0.5 & \color{green}{0.5} & \color{green}{0.0} \\ 0.0 & 0.0 & 0.0 & \color{green}{0.8} & \color{green}{0.2} \\ \hline 0.0 & 0.0 & 0.0 & 1.0 & 0.0 \\ 0.0 & 0.0 & 0.0 & 0.0 & 1.0 \end{array} \right]$$
Temps moyen avant état absorbant depuis $i$ =
somme des éléments de la $i^{eme}$ ligne de $N$.
Probabilité d'être absorbé en $j$ depuis $i$ =
coefficient $(i,j)$ de $B = N R$.
Avec PyDTMC
> mc.absorption_times
array([2.05, 1.5 , 1. ])Environ 2 "temps" avant un état absorbant depuis le niveau 1. "1.5" depuis le niveau 2, et 1 depuis le 3.
> mc.absorption_probabilities
array([[0.93, 0.9 , 0.8 ],
[0.07, 0.1 , 0.2 ]])Probabilité autour de 0.9 de perdre si on commence au niveau 1 ou 2. 0.8 / 0.2 logique (pourquoi ?)
Propriété "fondamentale"
Le coefficient d'indices $(i, j)$ de $P^n$ = probabilité d'atteindre $j$ au bout de $n$ pas depuis $i$.
Note : il pourrait aussi y avoir des états non absorbants mais visités "une infinité de fois" : cf. suite :)
Présentation détaillée (hors programme).
Chaînes non absorbantes
Exemple : état = niveau à Tetris (vitesse...)
Deux possibilités :
- passer au niveau suivant (s'il y en a un).
- revenir au niveau 1 (si on perd).
Supposons 4 états (= 4 niveaux).
Chemin possible : 1, 2, 3, 4, 1, 2, 1
Probabilités de transition ?
Matrice $P \Leftrightarrow$ graphe de transition
$$\begin{pmatrix} 0.3 & 0.7 & 0.0 & 0.0\\ 0.4 & 0.0 & 0.6 & 0.0\\ 0.6 & 0.0 & 0.0 & 0.4\\ 0.8 & 0.0 & 0.0 & 0.2 \end{pmatrix}$$
import pydtmc as m
P = [
[0.3, 0.7, 0.0, 0.0],
[0.4, 0.0, 0.6, 0.0],
[0.6, 0.0, 0.0, 0.4],
[0.8, 0.0, 0.0, 0.2]]
mc = m.MarkovChain(P,
['1','2','3','4'])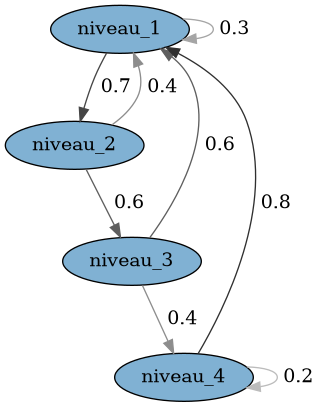
Définitions, propriétés
$P^n$ = matrice des transitions en $n$ étapes.
$P$ est régulière si $\exists n / P^n > 0$
# Test :
> mc.is_ergodic
TrueSi $P$ est régulière, $\exists ! w / w P = w$
$w$ = distribution stationnaire.
$\propto$ temps moyen passé dans chaque état.
> mc.stationary_distributions
[array([0.42918455, 0.30042918, 0.18025751, 0.09012876])]Temps d'atteinte ($P$ régulière...)
Temps moyen depuis $i$ avant de revenir en $i$ ( = $r_i$) ?
> mc.mean_recurrence_times
array([ 2.33, 3.32857143, 5.54761905, 11.0952381 ])$r_i = 1 / w_i$
Temps moyen pour arriver à $j$ en partant de $i$ ?
> mc.mean_first_passage_times_between(['1'], ['4'])
12.619047619047619Astuce = considérer 4 comme absorbant.
$\rightarrow$ Retour au cas précédent.
Promenade
m.plot_walk(mc, 20, '1', plot_type='sequence')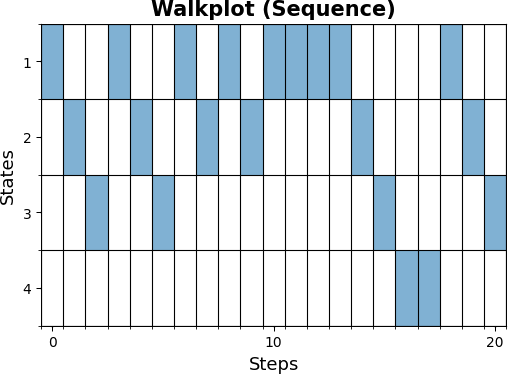
Approche prédictive I
On vous donne une (longue) suite d'états.
Déterminer une chaîne y correspondant.
mc_est = mc.fit_walk(
'map',
['1','2','3','4'],
mc.walk(100, '1'))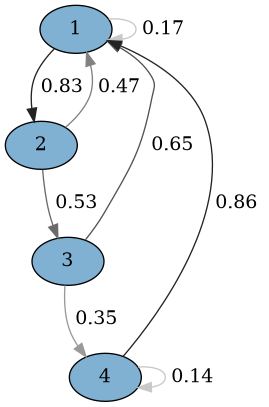
Approche prédictive II
On vous donne une suite d'états.
A-t-elle été générée par la chaîne $mc$ ?
> mc.walk_probability(
['1','2','3','1','2','3','1','2','1','2'])
0.012446783999999994
> mc.walk_probability(
['1','1','1','2','3','4','4','4','4','4'])
2.4191999999999995e-05Application : détection d'anomalies.
Exercice 1
Le chat "markovien" Gribouille ne réalise que 3 actions dans sa journée : dormir, manger et jouer.
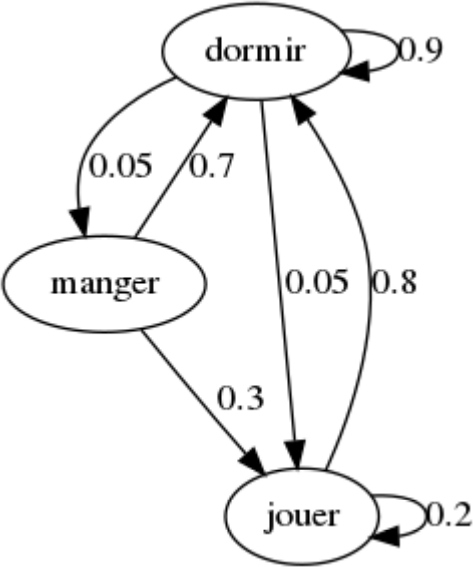
- À $t=5$, Gribouille dort. À $t=8$, quelle est la probabilité qu'il joue ?
- À $t=0$, Gribouille mange. À $t=12$, quelle est la probabilité qu'il dorme ?
- Calculez la distribution stationnaire.
- À $t=10$, Gribouille dort. Au bout de combien de temps en moyenne mangera-t-il ?
Exercice 2
Pour sortir de prison sous caution, Albert doit
payer 8€. Il n'a que 3€ sur lui.
Un gardien lui propose un jeu (en plusieurs tours) :
- Si Albert parie A€, il gagne A€ avec probabilité 0.4
- Sinon, il perd A€ avec probabilité 0.6
Probabilité qu'Albert sorte de prison ainsi ?
Stratégie optimale ?
Suggestion de corrigé
Exercices des examens précédents
Voir {2021,2022,2023}/examen/ par ici.
Détection d'anomalies
Lisez et comprenez cet article dans les grandes lignes : inutile de s'attarder sur les détails.
Rock-Paper-Scissor(-Lizard-Spock)
Implémentez des joueurs (aléatoires) de pierre-feuille-ciseaux(-lézard-Spock, éventuellement) suivant plusieurs stratégies en modélisant la situation par une chaîne de Markov.
Jouez contre eux (sans savoir lequel est votre adversaire) : quel est le plus difficile à battre ?
Note : considérer un état = une action.
RPSLS - suite
La fonction walk() du module PyDTMC peut être utile (sinon c'est assez simple à réécrire).
Implémentez ensuite un joueur adaptatif, qui construit une chaîne de Markov au fur et à mesure que vous jouez contre lui. Il doit sélectionner les actions ayant le plus de chances de vous battre.
Intégration
Lisez (le plus possible) et comprenez au moins comment les chaînes de Markov sont utilisées dans cet article.
Brouillon de corrigé
Version JupyterVersion HTML
Note "hors programme"
Je n'ai pas parlé de chaînes de Markov...
- à temps continu,
- à temps discret mais espace d'état infini,
- dont la matrice de transition dépend du temps.
Ces trois situations sont évidemment intéressantes mais nécessitent + de rappels mathématiques. Voir par exemple Probabilités et processus stochastiques (Yves Caumel 2011).