Objectif
Diviser les données en $K$ groupes
Idéalement, les individus sont
- (très) similaires dans un même groupe.
- (très) différent de ceux des autres groupes.
Groupe = cluster (= classe)
Distance inter-points
Dans tout ce cours on n'utilisera que la distance euclidienne.
Exemple :
$d((0,3), (2,1)) = \sqrt{(0 - 2)^2 + (3 - 1)^2}\\
\quad \quad \quad \quad \quad \quad \, = \sqrt(8)$
En général utiliser les distances au carré suffit.
Algorithme "CAH"
Classification Ascendante Hiérarchique
En anglais : "Agglomerative Hierarchical Clustering"
$\Rightarrow$ Les groupes sont agglomérés (= fusionnés) petit à petit,
en considérant initialement $n$ groupes.
| Petal.Length | Petal.Width |
|---|---|
| 1.5 | 0.2 |
| 1.4 | 0.2 |
| 4.7 | 1.4 |
Avec R
data = matrix(c(1.5,1.4,4.7, 0.2,0.2,1.4), ncol=2)
distances = dist(data)
h = hclust(distances)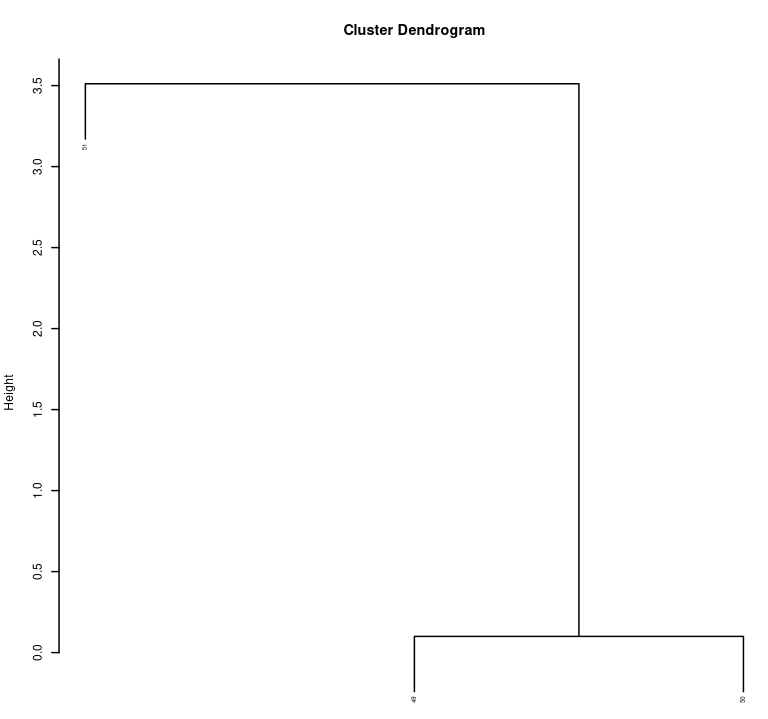
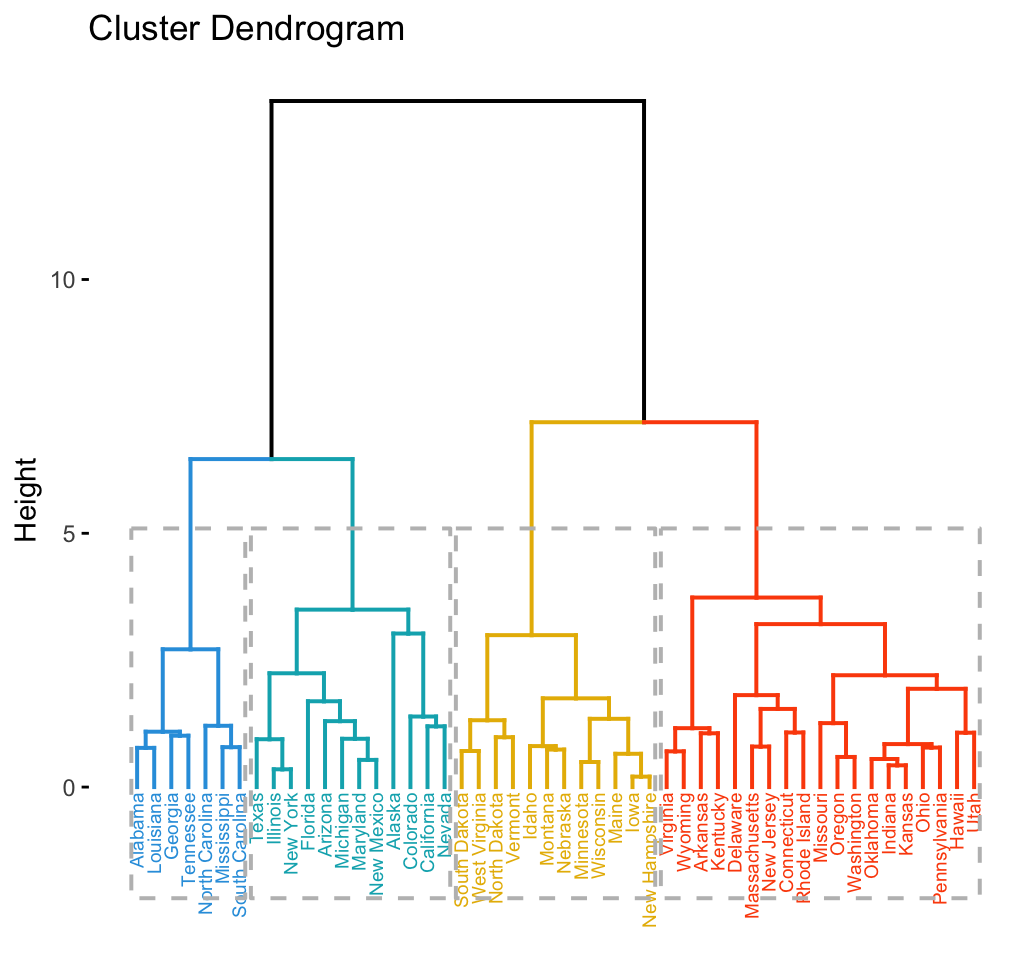
Dendrogramme : mode d'emploi
Hauteur entre deux fusions = "coût"
On "coupe" en général juste avant une division très coûteuse. Évident sur l'exemple :
# Coupe pour garder deux groupes
> cutree(h, 2)
49 50 51 #indices des individus
1 1 2 #numéros des clustersSouvent moins clair $\Rightarrow$ choix
Données iris
data = iris[,-5]
distances = dist(data)
h = hclust(distances)
#cutree(h, 2) ou cutree(h, 3) ...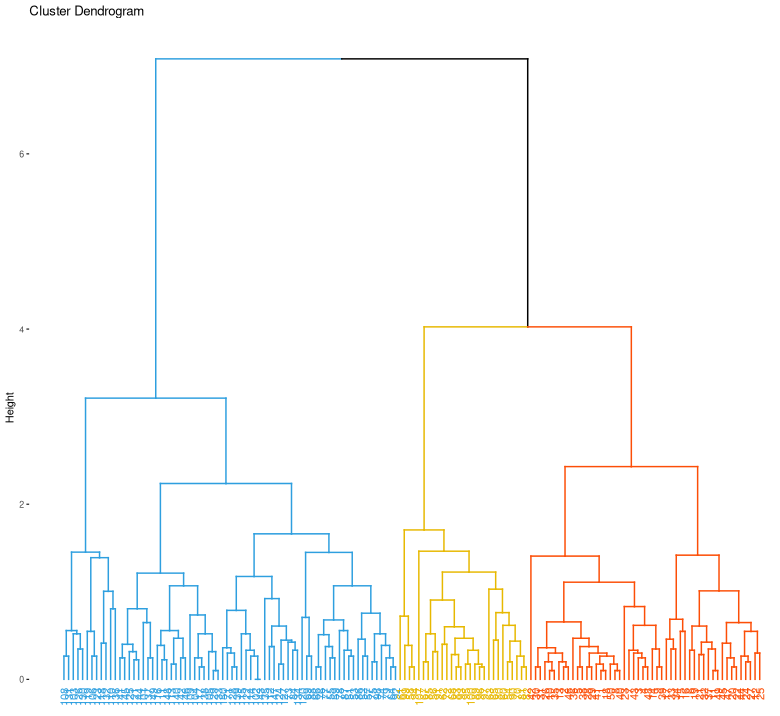
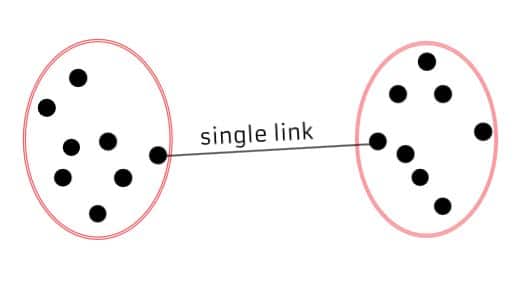
Distance inter-groupes I
Idée 1 = "single-linkage"
Distance entre les deux points les plus proches.
Distance inter-groupes II
Idée 2 = "complete linkage"
Distance entre les deux points les plus éloignés.
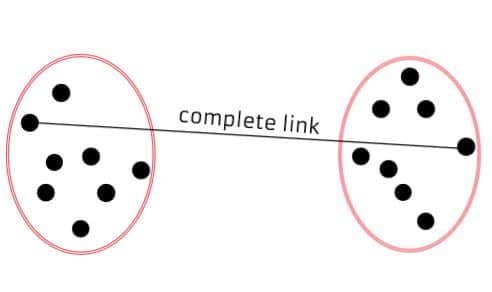
Distance inter-groupes III
Idée 3 = "Ward linkage"
→ Minimiser l'augmentation de l'inertie intra-classes.
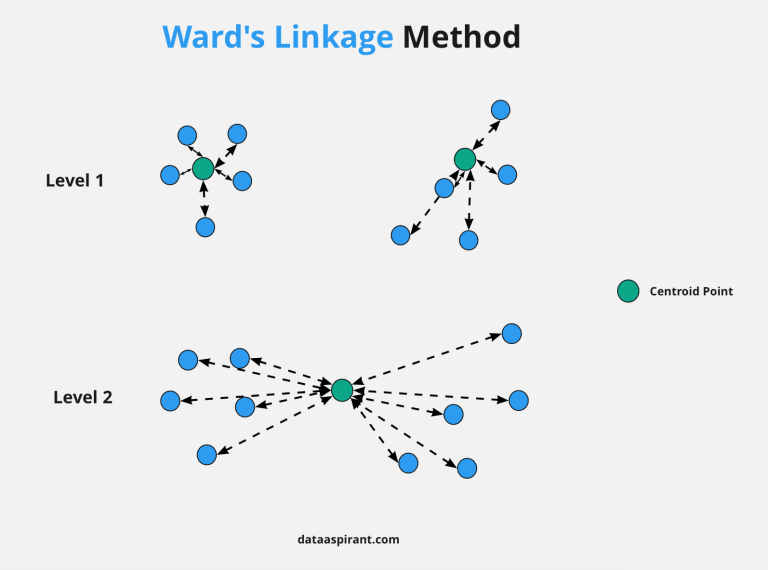
Définition des inerties inter/intra, à $n$ points
Inertie totale (constante !) : $I = \sum_{i=1}^{n} \| x_i - g \|^2$ avec $g$ le centre (moyenne par composante).
Inertie intra-classe : $I_I = \sum_{k=1}^{K} \frac{n_k}{n} I_k$ avec $n_k$ le nombre d'éléments du cluster $k$, et $I_k$ son inertie.
Inertie inter-classes : $I_E = \sum_{k=1}^{K} \frac{n_k}{n} \| g_k - g \|^2$ avec $g_k$ le centre du cluster $k$.
Propriété : $I = I_E + I_I$.
Résumé de l'algorithme
- Choix d'une mesure de distance inter-groupes
- Considérer chaque individu comme un groupe
- Calculer les distances inter-groupes
- Fusionner les deux clusters les plus proches
- Revenir en 3. s'il reste $\geq 2$ groupes
Exercice
Considérant les points (5,8), (1,6), (7,5), (4,2) et (6,1), appliquez l'algorithme du clustering hiérarchique en choisissant la distance single link(age).
Obtient-on le même résultat avec complete linkage ?
Algorithme "k-médoïdes"
Idée : définir $K$ centres de classes $c_1, \dots, c_K$.
Groupe $i$ = individus proches de $c_i$.
Pseudo-code
Entrée = matrice de dissimilarités.
- Choisir "arbitrairement" $K$ centres initiaux
- Assigner chaque point au médoïde le plus proche
- Recalculer les centres (médoïdes) $c_i$ :
$c_i$ = point minimisant la somme $\sum_{x} d(x, c_i)$ - Si les centres ont changé, revenir en 1.
Problème : l'étape 2. est (très) lente.
Illustration en vidéo. En hindi... mais très claire !
Exemple I
library(cluster)
p = pam(iris[,-5], 3)
# Tracé des clusters pour chaque paire de variables
plot(iris, col=p$clustering)
# Tracé dans le premier plan ACP
library(factoextra)
fviz_cluster(p)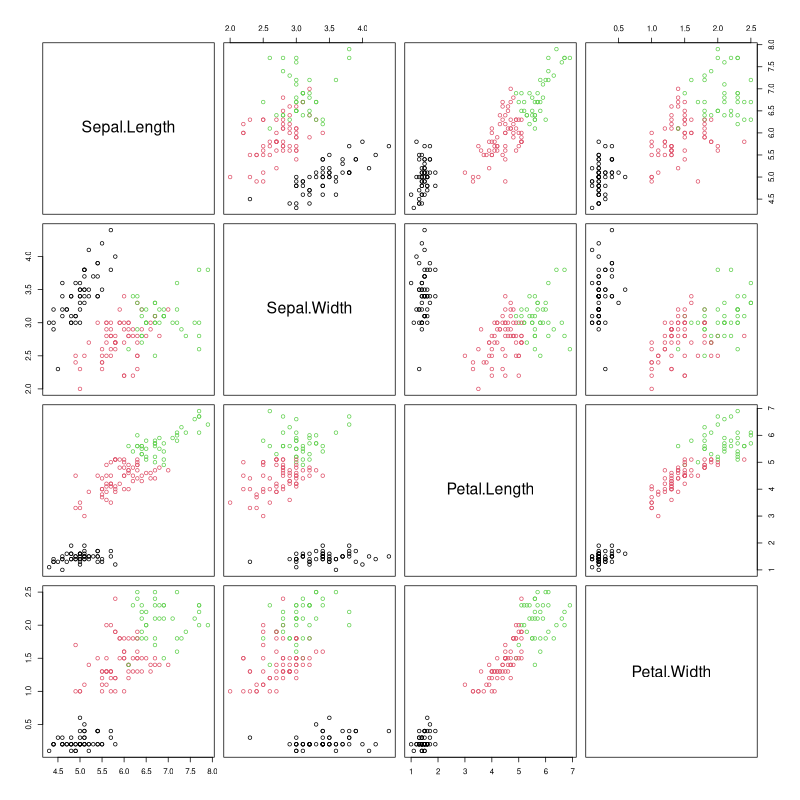
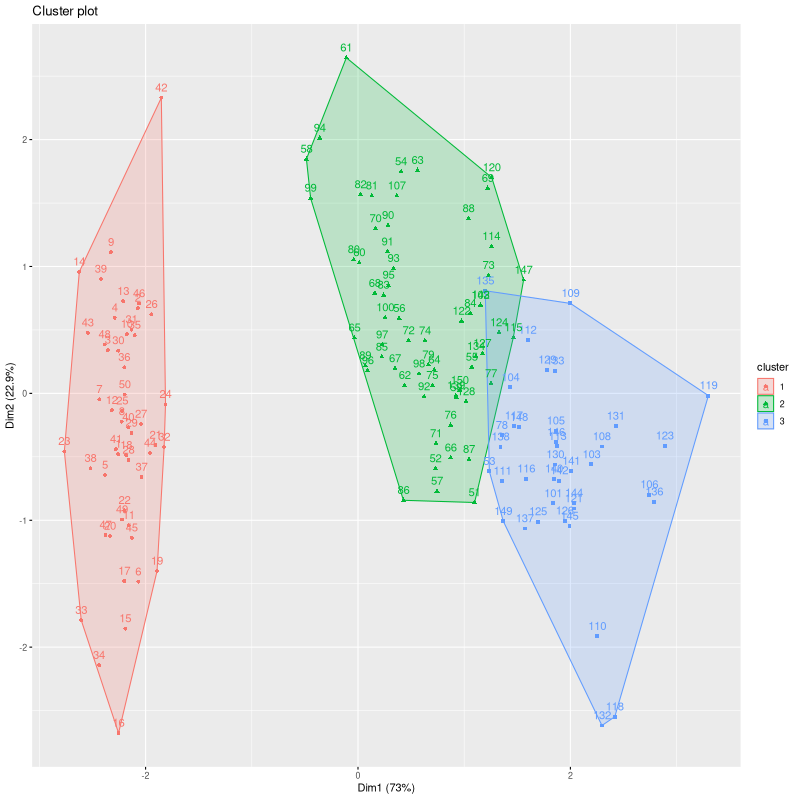
Exemple II
p = pam(scale(USArrests), 4)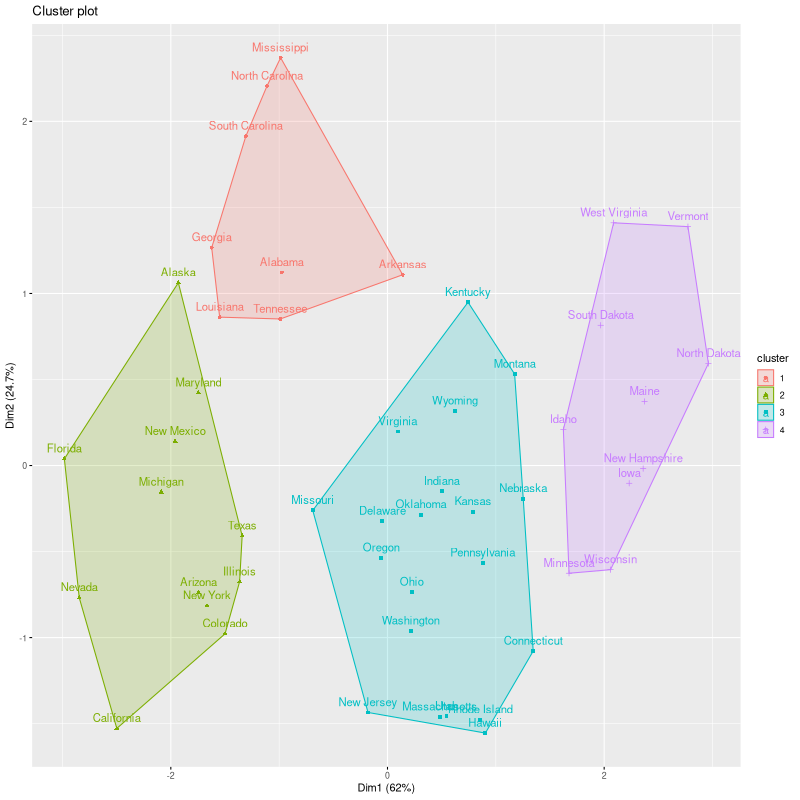
Bilan
Pros
- Algorithme robuste
- Classe des données de tout type (car ne prend qu'une matrice de dissimilarités en entrée)
Cons
- Inapplicable à de grands jeux de données
- Suppose des clusters relativement "sphériques"
Exercice
Points :
$(0, 0)$
$(1, 0)$
$(0, 2)$
$(2, 1)$
$(1, 3)$
$K = 2$
Centres initiaux $(0, 0)$ et $(1, 0)$
Algorithme "k-means"
Idée : définir $K$ centres de classes $c_1, \dots, c_K$.
Groupe $i$ = individus proches de $c_i$.
Différence avec $k$-médoïdes :
$c_i$ n'appartient pas forcément aux données !
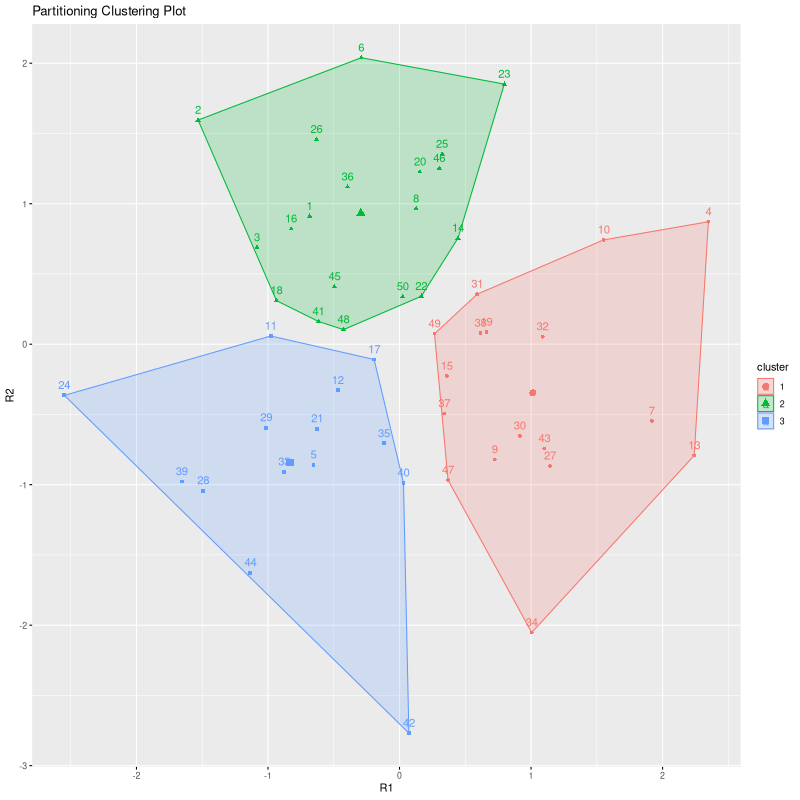
Pseudo-code
Entrée = matrice (numérique) des individus en lignes
- Choisir "arbitrairement" $K$ centres initiaux
- Assigner chaque point au centroïde le plus proche
- Recalculer les centres (centroïdes) $c_i$ :
$c_i$ = moyenne des éléments du cluster
(sur chaque coordonnée) - Si les centres ont changé, revenir en 1.
Illustration en vidéo. Source: https://vimeo.com/110060516
Exemple
k = kmeans(scale(USArrests), 4)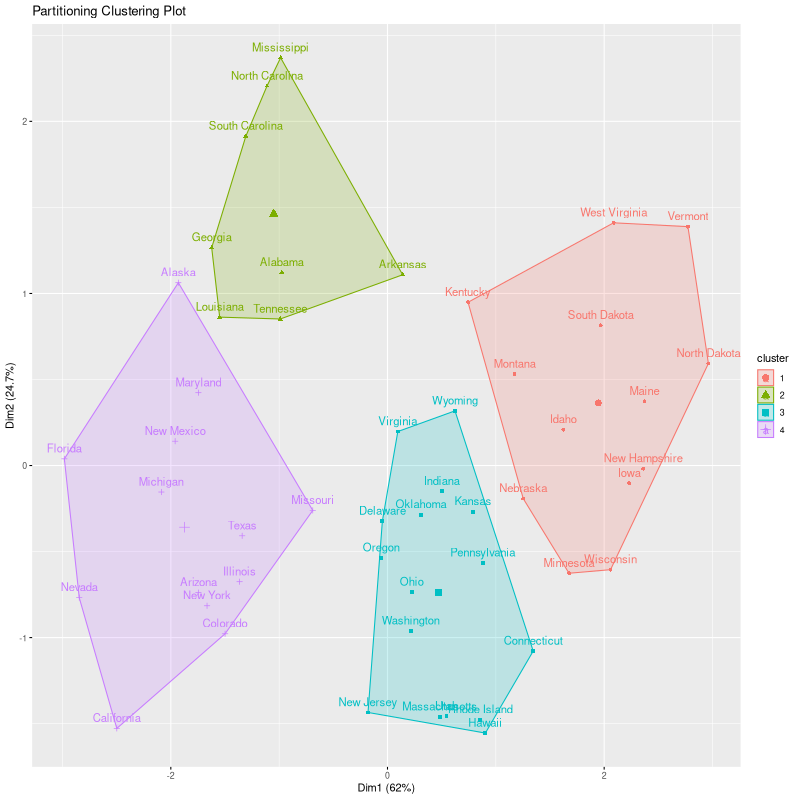
Bilan
Pros
- Algorithme rapide
- Applicable à de (très) grands jeux de données
Cons
- Sensible aux outliers
- Suppose des clusters relativement "sphériques"
Exercice
Mêmes points que pour k-medoids
$K = 2$
- Centres initiaux $(1, 0.5)$ et $(0.5, 2.5)$
- Centres initiaux $(0.5, 1)$ et $(1.5, 2)$
Validation du clustering
Vrais groupes connus :
calcul du taux de "bien classés"
Vrais groupes inconnus.
- Critères géométriques relatifs à l'inertie.
Voir ?clusterCrit::intCriteria - Relancer l'algorithme avec $\neq$ paramètres.
Si résultats similaires : stabilité.
Voir ?clusterCrit::extCriteria - Apprendre la relation individu $\rightarrow$ groupe.
Si bon taux de classification : confiance.
Données iris : qualité de classification
> dict = list("setosa"=1, "versicolor"=2, "virginica"=3)
> ref = unlist( dict[ iris[,5] ] )
> library(clusterCrit) #NOTE: installation manuelle
> k = kmeans(iris[,-5], 3)
> clusterCrit::extCriteria(ref, k$cluster, 'Jaccard')
0.6958588
> h = hclust(dist(iris[,-5])) #default: complete-linkage
> clusterCrit::extCriteria(ref, cutree(h, 3), 'Jaccard')
0.622282
> h = hclust(dist(iris[,-5]), method='ward.D')
> clusterCrit::extCriteria(ref, cutree(h, 3), 'Jaccard')
0.7248Conclusion : mauvaise adéquation (pourquoi ?).
Distance de Ward "mieux" que complete-link ici.
Critère géométrique
> library(clusterCrit)
> k = kmeans(iris[,-5], 3)
> dm = as.matrix(iris[,-5])
> clusterCrit::intCriteria(dm, k$cluster, 'Silhouette')
0.5555218
> h = hclust(dist(iris[,-5]), method='single')
> clusterCrit::intCriteria(dm, cutree(h, 3), 'Silhouette')
0.6713506Indice 'Silhouette' dans $[-1, 1]$, mieux si proche de 1.
Donc la partition trouvée par hclust est meilleure ?!
Exercice : y réfléchir :)
Définition des indices
Tous les détails sont sur la vignette.
Indice de Jaccard : TODO
Indice "Silhouette" : TODO
Évaluation de la stabilité
> library(clusterCrit)
> k1 = kmeans(iris[,-5], 3)
> k2 = kmeans(iris[,-5], 3)
> clusterCrit::extCriteria(k1$cluster, k2$cluster, 'Jaccard')
0.4967985On est loin de 1 (sur cet essai) $\Rightarrow$
Grande sensibilité au choix de centres initiaux.
Voir argument 'nstart' pour améliorer ça.
Exercice 0
Exercices "Clustering" des examens passés (et entraînements) par ici.
Voir les dossiers {2022,2023}/examen/
Exercice 1
Récupérez le jeu de données "Pokemons"
Appliquez les algorithmes présentés
pour différentes valeurs de $K$.
Visualisez les résultats.
Essayez quelques critères de validation.
Voir clusterCrit.pdf
Exercice 2
Récupérez quelques jeux de données artificiels sur cette page. (La fonction read.arff() du package foreign est pratique).
Faites tourner les algorithmes pour les valeurs de $K$ apparentes, et commentez/expliquez les résultats.
Suggestion de "corrigé"
Exercices type examen
grid_max <- 9
genExo <- function(n) {
dat <- matrix(sample(1:grid_max, 2*n, replace=TRUE), ncol=2)
plot(dat, pch=19) ; dat
}
genCtrs <- function(K) {
matrix(sample(1:grid_max, 2*K, replace=TRUE), ncol=2)
}Appelez "genExo(7)" (par exemple, $n = 6$ ou 7 est ok), puis "genCtrs(2)" (pour $K = 2$ ; essayer aussi avec $K = 3$).
Faites tourner l'algorithme des k-means et CAH sur les données. Générez un autre jeu de données. Recommencez.