La propagation des ondes : des formes simples aux vibrations chaotiques
Avec Stéphane Nonnenmacher
Nous avons l'habitude d'entendre une onde sonore, moins de la visualiser. Or une onde se propageant dans une cavité fermée donne parfois lieu à des motifs étonnamment complexes. Stéphane Nonnenmacher étudie la propagation des ondes sur des surfaces de formes simples; en dépit de cette simplicité géométrique, ces ondes dévoilent, à haute fréquence, des comportements “chaotiques”.
Les vibrations d’un tambour : des fréquences imprévisibles

Prenons l’exemple d’un tambour. Lorsqu’on frappe celui-ci, la membrane se met à vibrer, selon certaines fréquences spécifiques au tambour. En vibrant, la membrane créée du mouvement dans l'air environnant, produisant une onde sonore qui sera finalement détectée par notre oreille. Nous pouvons ainsi "entendre" les fréquences de vibration (ou "fréquences propres") du tambour. De même lorsqu’on pince une corde de guitare, celle-ci vibre selon plusieurs fréquences. Elle produit une note fondamentale, appelée fréquence de base, ainsi que des harmoniques (des notes plus aiguës), qui sont des multiples de cette fréquence de base.
Au contraire, les fréquences propres du tambour ne sont en général pas multiples de sa fréquence fondamentale, de sorte que le son qui perçu n'est pas aussi "net" que celui d'une corde de guitare. Les valeurs de ces fréquences propres dépendent intimement de la forme du tambour.
Visualiser la propagation des ondes : l’expérience de Chladni
Au delà des fréquences de vibration, il est également intéressant de visualiser les ondes se propageant à travers la membrane du tambour; en effet, la vibration n'est pas uniforme sur toute la surface.

© Matemateca (IME/USP)/Rodrigo Tetsuo Argenton
Au XVIIIe siècle, Ernst Chladni a illustré ce phénomène en saupoudrant du sable sur une plaque métallique qu'il faisait vibrer avec un archet de violon (la plaque fait office de membrane de tambour). A une fréquence propre donnée, le sable se déplace vers les zones appelées "nœuds", où la plaque ne vibre pas. Cette expérience permet de visualiser la répartition de l’énergie vibratoire à travers la surface, pour le « mode propre de vibration » observé.
La manière dont cette énergie se répartit varie selon la forme du tambour, et la fréquence propre observée. Plus cette fréquence est élevée, plus la répartition peut devenir complexe.

© Arnd Baecker
Prenons un tambour standard, circulaire. La répartition de l’énergie dépend fortement de la fréquence propre qu’on considère: l’énergie peut se concentrer plus vers le centre, ou bien plutôt près du bord, ou encore de manière équilibrée sur toute la membrane. Grâce à la symétrie de la forme circulaire, ces répartitions variées sont bien comprises mathématiquement. Pour la même raison, les nœuds de vibration forment toujours des motifs réguliers.
Formes irrégulières et vibrations chaotiques

© Eduardo Vergini
Si l’on prend maintenant des formes de tambour qui restent simples, mais moins symétriques que le cercle, les motifs vibratoires deviennent plus complexes. Stéphane Nonnenmacher s’intéresse particulièrement à des formes qui engendrent des modes vibratoires « chaotiques ».
C'est le cas par exemple d’un tambour en forme de stade, une forme intermédiaire entre le cercle et le rectangle. La propagation de l’onde sur ce tambour-stade est plus complexe que dans le cas du cercle. Pour comprendre l’origine de cette complexité, imaginons une table de billard ayant cette forme de stade, sur laquelle une boule de billard avance et rebondit indéfiniment sur ses bords. Du fait de la forme de stade de la table, les rebonds successifs deviennent rapidement imprévisibles : on parle alors, pour cette boule de billard, de dynamique chaotique.
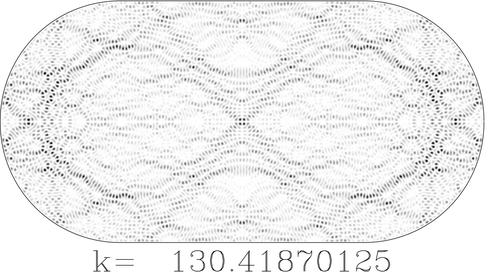
© Eduardo Vergini
Les recherches de Stéphane Nonnenmacher se concentrent sur ces phénomènes de chaos ondulatoire. À haute fréquence, les motifs vibratoires deviennent extrêmement complexes, avec des motifs géométriques fins et des oscillations rapides. Malgré cette complexité, il s’avère que dans l’ensemble, les vibrations se répartissent de façon plutôt uniforme sur la surface du tambour-stade, sans qu’une zone particulière ne concentre l’énergie. Etonnamment, cette répartition uniforme de l’onde peut s’expliquer à partir de la dynamique chaotique de la boule de billard !
Ondes lumineuses et électro-magnétiques
Des expériences similaires peuvent être menées avec des rayons laser ou des micro-ondes piégés dans des cavités de formes variées. Bien que les ondes électromagnétiques – comme par exemple les ondes lumineuses – soient de nature physique différente des ondes acoustiques, elles obéissent à des équations mathématiques similaires.
Ces recherches permettent de modéliser par exemple la propagation de la lumière dans une fibre optique de section non circulaire, ou dans des micro-lasers de diverses formes. Elles ont des applications dans des domaines comme l'ingénierie ou la physique, pour optimiser les systèmes de communication, comprendre la propagation des sons dans des environnements complexes.
Ce qui ressort des travaux sur le chaos ondulatoire, c’est l’idée que les vibrations, même dans des systèmes apparemment simples comme un tambour-stade, peuvent mener à des répartitions d’énergie très complexes quand on monte à haute fréquence.
Stéphane Nonnenmacher est Professeur à l'Institut de Mathématiques d'Orsay, spécialisé en analyse mathématique et équations aux dérivées partielles.
