L'unité des mathématiques : quand la géométrie algébrique éclaire la théorie des nombres

Avec David Harari

Aux origines de la théorie des nombres

 

 

 

Depuis l'Antiquité, les mathématiciens se sont passionnés pour l'étude des nombres. Les premiers auxquels ils se sont intéressés sont les nombres entiers (positifs ou négatifs) : 1,2,3, -12, 15, 135...  des valeurs que l'on manipule quotidiennement. Ces nombres peuvent être additionnés, soustraits ou multipliés tout en restant des nombres entiers.

Cependant, lorsqu'il a fallu diviser ces nombres, de nouveaux types de nombres ont été introduits : les nombres rationnels, tels que 1/4, 2/3, 5/7, 105/12, etc. Ces nombres se comportent de manière similaire aux entiers et peuvent également être additionnés, multipliés ou divisés. Les nombres rationnels forment ce que l'on appelle en mathématique un corps, possédant une structure fascinante, qui fait l'objet d'études approfondies.

 

 

 

Dans l'Antiquité, les mathématiques étaient principalement appliquées à la géométrie. Les mathématiciens de l'époque se sont posé une question que nous connaissons bien : quelle est la longueur de la diagonale d'un carré de côté 1 ? Ils ont formulé le célèbre théorème de Pythagore : AB² = AC² + BC² . Ils se sont alors aperçus qu'il était impossible d'exprimer la longueur de cette diagonale avec des nombres entiers ou rationnels. Cette découverte a suscité de nombreuses interrogations parmi les savants de l’époque.

 

Quand les équations défient les algorithmes

C’est précisément sur ce type de question que se concentre David Harari : déterminer si certaines équations peuvent avoir des solutions en nombres entiers ou en nombres rationnels. David Harari travaille sur les équations polynomiales : des équations où les inconnues peuvent être additionnées, soustraites ou multipliées, mais pas divisées.

Or déterminer si une équation a une solution en nombre entier peut sembler simple, mais c'est en réalité un défi considérable. De nombreux mathématiciens ont tenté d’élaborer des algorithmes pour résoudre ce problème. Cependant, dans les années 1970, il a été démontré qu'il n'existe pas de méthode générale pour savoir si une équation donnée a des solutions en nombres entiers.  Quant aux nombres rationnels, le problème reste ouvert : il semble également qu’aucun algorithme général ne puisse déterminer de manière systématique si une équation a des solutions rationnelles.

 

De nouvelles méthodes avec la géométrie algébrique

Face à ce défi, David Harari s'est tourné vers des familles spécifiques d'équations présentant des caractéristiques particulières. Il travaille à concevoir un algorithme pour ces familles, afin de déterminer s'il existe des solutions en nombres entiers ou rationnels.

 

 

 

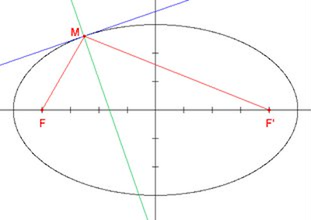
David Harari s'appuie sur les outils de la géométrie algébrique moderne, développée dans les années 1950, qui offrent un langage permettant d'analyser les équations non plus une par une, mais au sein d'une famille plus vaste. En étudiant les structures géométriques de ces familles, il parvient à mettre au point des méthodes pour explorer l’ensemble de leurs solutions. Les recherches de David Harari permettent ainsi de déterminer, pour certains types d’équations polynomiales, s'il existe des solutions en nombres entiers ou rationnels. De plus, il cherche à comprendre si ces solutions sont rares ou nombreuses.

Les travaux de David Harari illustrent parfaitement l'unité des mathématiques et leur évolution à travers les siècles. Des méthodes récentes issues de la géométrie algébrique permettent aujourd'hui de répondre à des questions millénaires, provenant d'un autre domaine des mathématiques : la théorie des nombres.

David Harari, professeur à l'Université de Paris-Saclay (Orsay), est spécialiste d'arithmétique et de géométrie algébrique.