Géométrie birationnelle : l’essence cachée des formes
Avec Susanna Zimmermann
En mathématiques, de nombreuses avancées ont été permises grâce au développement récent de la géométrie algébrique, qui établit un lien entre des équations et des formes géométriques. En étudiant ces formes géométriques, les mathématiciens peuvent extraire des informations essentielles sur les équations sous-jacentes.
Parmi les chercheurs qui explorent ces territoires mathématiques, Susanna Zimmermann se concentre sur la géométrie birationnelle, une branche de la géométrie algébrique qui cherche à comprendre comment les formes géométriques peuvent être modifiées tout en conservant leurs propriétés fondamentales.
Transformer tout en conservant l’essentiel
Imaginez que vous ayez une feuille de papier. Vous pouvez la plier, la tordre, la déformer de différentes manières, mais tant que vous ne la déchirez pas ou ne la collez pas, elle reste essentiellement la même feuille. C'est le principe de transformation sans destruction, qui est au cœur de la géométrie birationnelle. A quelles transformations complexes puis-je soumettre mon objet sans perdre ses propriétés essentielles.
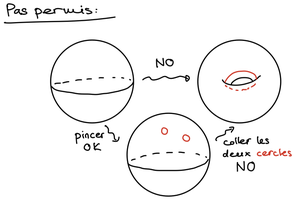
Prenons un exemple simple : une sphère. Vous pouvez faire tourner cette sphère, l’écraser, lui faire des creux, la déformer. Ces transformations, bien que visuellement différentes, préservent certaines caractéristiques géométriques de base. Toutefois, si vous faites deux trous dans la sphère et la transformez en une sorte de donut (en collant les deux trous de long de leur bord), ou ce que les mathématiciens appellent un tore, les propriétés fondamentales changent. Les objets qui ont le même nombre de trous ont des propriétés similaires entre eux. Ce type de trou ‘tore’ constitue un invariant qui permet de distinguer et classer les objets géométriques les uns par rapport aux autres.
Classer et comprendre les transformations
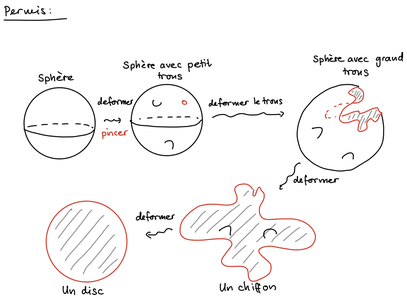
Un des objectifs des travaux de Susanna Zimmermann est de trouver d’autres invariants pour distinguer des objets géométriques entre eux. Ainsi elle analyse ce qui se passe si l’on transforme un objet pour le rendre plus grand, ou irrégulier. Si l’on prend par exemple un ballon de baudruche et on ouvre le nœud du ballon pour le faire dégonfler, l’objet est en apparence très différent et pourtant, ses propriétés mathématiques ne changent pas tant que ça.
Susanna Zimmermann explore ainsi toutes les déformations possibles d’un objet géométrique, tout en cherchant les invariants. Ses recherches permettent de mieux comprendre les relations profondes entre des objets géométriques apparemment très différents.
Les apports de des travaux de Susanna Zimmermann sont nombreux. En effet, ces formes géométriques sont liées à des équations mathématiques. En organisant et classant ces formes, la géométrie birationnelle permet de mieux organiser et comprendre de vastes familles d’équations mathématiques. Un des objectifs de la géométrie birationnelle est de simplifier la compréhension des équations complexes en les associant à des objets géométriques plus simples.
Application en cryptographie
Les découvertes en géométrie birationnelle ont des applications dans de nombreux domaines des mathématiques pures, mais aussi dans des disciplines appliquées comme la cryptographie. Lorsqu’on encrypte des données, on va créer un code pour chacune des lettres ou des mots, dont on donnera la clef au destinataire. L’objectif des cryptographes est de rendre cette transformation du texte, ou encodage, difficilement reversible pour quelqu’un qui n’aurait pas la clef, de sorte qu’il ne puisse pas revenir au texte initial. On peut faire un parallèle entre cet transformation - ou encodage - du texte, et les transformations d’objets géométriques.
Grâce au travaux de Susanna Zimmermann et d’autres mathématiciens, on connait l’ensemble des transformations qui maintiennent les propriétés de mon objet, ou de mon texte. On peut donc choisir parmi cet ensemble des modifications spécifiques plus difficilement reversibles, celles qui permettent de mieux cacher la manière dont a été créé le code.
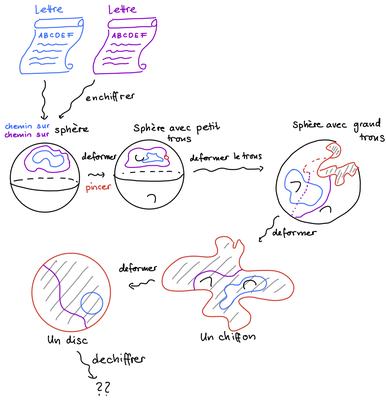
Imaginons que le texte que nous voulons encoder soit représenté par un fin chemin qui fait le tour d’un ballon de baudruche. Ce chemin est l’information de base — c’est le texte original, non crypté. Maintenant, pour protéger ce texte, nous devons modifier notre ballon, et le chemin, de manière à ce qu'ils deviennent plus difficile à identifier. Cependant, il faut que ces transformations préservent certaines propriétés fondamentales, mon chemin doit par exemple rester un cercle.
Lorsque nous faisons des creux ou des bosses sur le ballon, nous modifions la forme du chemin qui entoure le ballon. C’est comme si nous avions appliqué une première étape d’encodage : le chemin a changé de forme, il devient plus difficile à suivre, mais il reste connecté et continue de faire le tour du ballon. Ce processus est un peu comme modifier les lettres d’un texte en un autre alphabet, mais en maintenant la structure générale du texte.
Poursuivons cette métaphore avec une étape supplémentaire. Supposons que nous décidions de faire un trou dans le ballon. Ce trou pourrait représenter une partie d’information que nous choisissons de cacher entièrement, comme une clef cryptographique ou une donnée essentielle à la déchiffrement du code. Il devient alors impossible de récupérer cette information ou de la retrouver à partir de la forme déformée du ballon.
Grâce à la géométrie birationnelle, on peut donc transformer des données de manière complexes tout en maintenant leurs propriétés essentielles cachées. De manière plus générale, ces recherches aident à révéler des connexions profondes entre des objets mathématiques apparemment différents. Ces connexions permettent aux mathématiciens d’aborder des problèmes complexes sous un nouvel angle et de résoudre des questions ouvertes depuis longtemps.
Susanna Zimmermann est professeure des universités à l'Université Paris-Saclay, spécialisée en géométrie algébrique et en géométrie birationnelle, où elle explore les transformations des variétés algébriques et leurs symétries
